
matematika
.doc
Ауыспа таңбалы
![]() қатарының жинақты болу шартын көрсетіңіз
қатарының жинақты болу шартын көрсетіңіз
Ж: а1> a2>…>an>… lim an=0
![]() дәрежелік қатардың жинақтылық
радиусын көрсетіңіз
дәрежелік қатардың жинақтылық
радиусын көрсетіңіз
Ж: R=1/lim
![]() қатарының абсолют жинақты
болу шартын көрсетіңіз Ж:
a1
+ a2
+ a3
+…+ an
+ … жинақты
қатарының абсолют жинақты
болу шартын көрсетіңіз Ж:
a1
+ a2
+ a3
+…+ an
+ … жинақты
$$$ 324
![]() қатарының шартты жинақты
болуының анықтамасы
қатарының шартты жинақты
болуының анықтамасы
Ж: аn қатар жинақсыз, ал
аn қатар жинақты
Ақиқат оқиғаның ықтималдығы тең:
Ж: 1
Атқыштың нысанаға тигізу ықтималдығы 0,7-ге тең. Оның нысанаға атқан екі оғының екеуінің де нысанаға тию ықтималдығын тап
Ж: 0,49
Ә(ә)
Әрбір 10 лоторея билетінің 2-еуі ұтысты. Кездейсоқ сатып алынған 5 билеттің 2-еуі ұтысты билет болу ықтималдығын тап
Ж: С25 (0,2)2 (0,8)3
Бернулли формуласын көрсет
(мұндағы
![]() -
-![]() оқиғасының бір тәжірибеде орындалу, ал
оқиғасының бір тәжірибеде орындалу, ал
![]() сол тәжірибеде орындалмау ықтималдықтары)
сол тәжірибеде орындалмау ықтималдықтары)
Ж: Pn(k)= Ckn pk qn-k
Монетаны (тиынды) екі рет лақтырғанда кемінде бір рет «герб» түсу ықтималдығын тап
Ж: 3/4
![]() функциясының Маклорен қатарына
жіктелуін көрсетіңіз
функциясының Маклорен қатарына
жіктелуін көрсетіңіз
Ж: ex=1+x+x2/x!+x3/3!+…+xn/n!+...
Егер сандық қатар
![]() жинақты болса, онда
жинақты болса, онда
Ж: lim an=0
Егер
![]() және
және
![]() қатарларының
қатарларының
![]() мүшелері үшін
мүшелері үшін
![]() теңсіздіктер орындалса, онда
теңсіздіктер орындалса, онда
Ж: bn қатарының жинақтылығынан аn қатардың жинақтылығы шығады
Егер
![]() болса, онда
болса, онда
![]() дәрежелік қатарының жинақтылық радиусы
неге тең?
дәрежелік қатарының жинақтылық радиусы
неге тең?
Ж: R=lim an/ an+1
Егер
![]() дәрежелік қатары нөлге тең емес
дәрежелік қатары нөлге тең емес
![]() нүктесінде жинақты болса, онда
нүктесінде жинақты болса, онда
Ж: |x| < |x0| тендігін қанағат-н барлық х-тер үшін абсолют жинақты
Егер дәрежелік
![]() - қатары
- қатары
![]() нүктесінде жинақсыз болса, онда ол
нүктесінде жинақсыз болса, онда ол
Ж: |х| > |х0| тендігін қанағат-н барлық х-тер үшін жинақсыз болады
Егер
![]() қатары жинақты болса, онда
қатары жинақты болса, онда
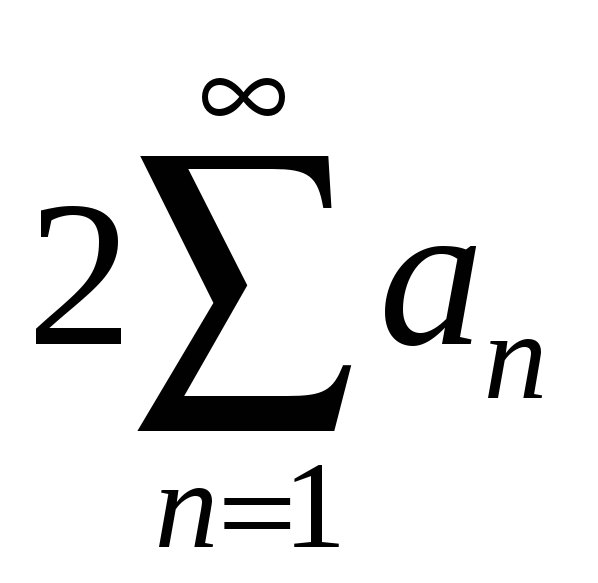 қатары туралы не айтуға болады?
қатары туралы не айтуға болады?
Ж: жинақты
Егер
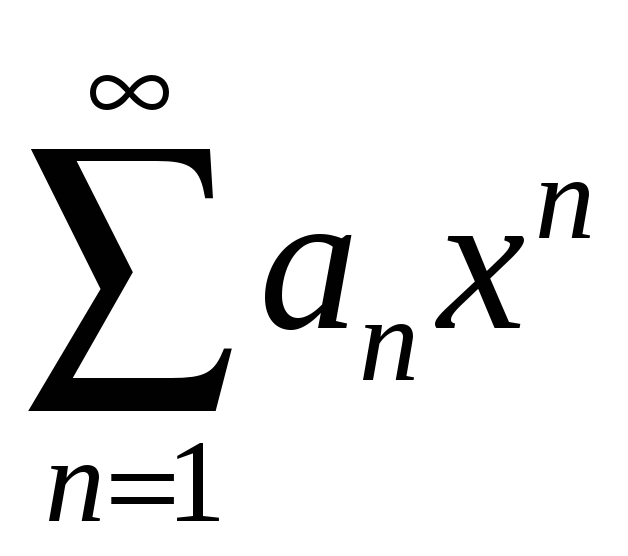 қатары
қатары
![]() нүктесінде жинақты болса, онда қатарЖ:
|х| < |x0|
болғанда әрбір х нүктесінде жинақты
нүктесінде жинақты болса, онда қатарЖ:
|х| < |x0|
болғанда әрбір х нүктесінде жинақты
Екі үйлесімсіз А және В оқиғаларының қосындысының ықтималдығы тең:
Ж: P(AB)=P(A)+P(B)
Екі тәуелсіз оқиғалардың көбейтіндісінің ықтималдығы тең:
Ж: P(AB)=P(A)*P(B)
Екі тәуелді оқиғалардың көбейтіндісінің ықтималдығы тең:
Ж: P(AB)=P(A)*PA(B)
Екі үйлесімді оқиғалардың қосындысының ықтималдығы тең:
Ж:P (A+B)=P(A)+P(B)-P(AB)
Екі аңшы түлкіге бір уақытта оқ атады. Әр аңшының түлкіге тигізу ықтималды 1/3-ге тең. Түлкінің атылған болу ықтималдығы неге тең?
Ж: 4/9
Екі атқыш бір-біріне тәуелсіз бір нысанаға оқ атқан. Бірінші атқыштың нысанаға тигізу ықтималдығы 0,7-ге, ал екіншісінікі – 0,6-ға тең. Нысанаға оқтың тиген болу ықтималдығын тап
Ж:0,88
Екі монетаны қатарынан лақтырғанда екеуінде де «герб» түсу ықтималдығы неге тең?
Ж: 1/4
![]() функциясының
функциясының
![]() нүктесінде Тейлор қатарына жіктелуін
көрсетіңіз
нүктесінде Тейлор қатарына жіктелуін
көрсетіңіз
Ж: f(a)+f/(a)/1!*(x-a)+f//(a)/2!*
(x-a)2+…+f(n) (a) / n!*(x-a)n+…
Г(г)
Гармоникалық қатарды көрсетіңіз
Ж: 1/n
Ж(ж)
Жәшіктегі бірдей 50 деталдың 5-і боялған. Кез келген детал алынды. Алынған деталдың боялған болу ықтималдығын табыңыз
Ж:0,1
Жәшікте 4 ақ және 8 қызыл шарлар бар. Жәшіктен кездейсоқ алынған шардың қызыл шар болу ықтималдығын тап
Ж: 2/3
Жәшікте 5 ақ, 4 жасыл және 3 қызыл шарлар бар. Жәшіктен кездейсоқ алынған шардың боялған шар болу ықтималдығын тап
Ж:7/12
Жәшікте 50 бірдей деталдар бар, оның ішінде 5 боялған кездейсоқ бір деталь алынсын. Осы алынған деталдың боялған детал болу ықтималдығы неге тең?
Ж: 0,1
X(x)
Х кездейсоқ шама биномиалдық
үлестіру заңдылығымен беріліп,
параметрлері
![]() және
және
![]() болса, онда оның санды сипаттамалары
М(Х) және Д(Х) тең:
болса, онда оның санды сипаттамалары
М(Х) және Д(Х) тең:
Ж:M (X)=1, D(X)=3/4
Х кездейсоқ шаманың үлестіру
заңдылығы:
![]() .
Математикалық үміті М(Х) тап
.
Математикалық үміті М(Х) тап
Ж: M(X)=6
Х-кездейсоқ шаманың дисперсиясы
D(X)=5.
![]() кездейсоқ шаманың дисперсиясын тап
кездейсоқ шаманың дисперсиясын тап
Ж:M(Z)=45
Т(t)
Толық ықтималдықтың формуласын көрсет
Ж: P(A) = P(H1) PH(A)+ P(H2) PH(A) +…+ P(Hn) PH (A)
Тұрақты шаманың математикалық үміті тең:
Ж:M (C)=C
Тұрақты шаманың дисперсиясы тең
Ж: D(C)=0
Тест жүргізілгенде студент 5 мүмкін болған жауаптардың біреуін кездейсоқ таңдайды. Бұл 5 жауаптардың тек қана біреуі дұрыс. Берілген екі тестке дұрыс жауап беруінің ықтималдығын тап
Ж: 1/25
Техникалық тексеру бөлімі 100 деталдың ішінен 5 қарамсыз детал табады. Кездейсоқ алынған деталдың жарамсыз пайда болу жиілігі неге тең?
Ж: W=0,05
Таңдама дисперсиясы
![]() тең (мұндағы
тең (мұндағы
![]() -
таңдама орта)
-
таңдама орта)
Ж: Db 1/n ni (xi-xb)2
Y(y)
![]() ,
,
![]() -
түрде берілген бірінші реттік
дифференциалдық теңдеуін не деп атайды?
-
түрде берілген бірінші реттік
дифференциалдық теңдеуін не деп атайды?
Ж: Бернулли теңдеуі
![]() функциясы үшін Маклорен
қатарының жалпы мүшесі
функциясы үшін Маклорен
қатарының жалпы мүшесі
Ж:f (n) (0)/n!*xn
4 карточкалардың әр қайсысына Б, Е, Н, О әріптері жазылған. Осы карточкаларды кездейсоқ қатар (бірінен кейін бірін) орналастырғанда «небо» деген сөздің жазылу ықтималдығын тап
Ж:1/24
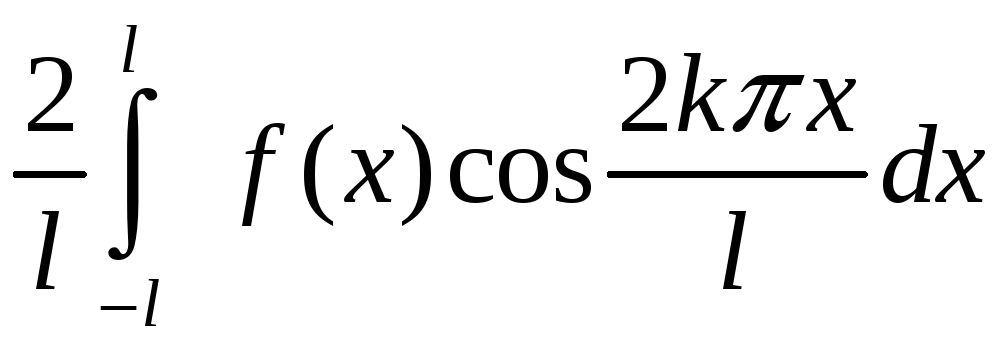 қатарының жинақталу аралығын
табыңыз
қатарының жинақталу аралығын
табыңыз
Ж: (-1; 1)
![]() функциясының Маклорен қатарына
жіктелуін көрсетіңіз (
функциясының Маклорен қатарына
жіктелуін көрсетіңіз (![]() кез
келген тұрақты сан)
кез
келген тұрақты сан)
Ж: (1+x)m = 1 + mx + m(m-1) / 2! * x2 +m(m-1) (m-2) / 3! * x3 + …|x| < 1
p –
параметрінің қандай мәндерінде
![]() - Дирихле қатары жинақты болады?
- Дирихле қатары жинақты болады?
Ж: p>1
Интегралдық функция арқылы
берілген Х кездейсоқ шаманың математикалық
үмітін тап
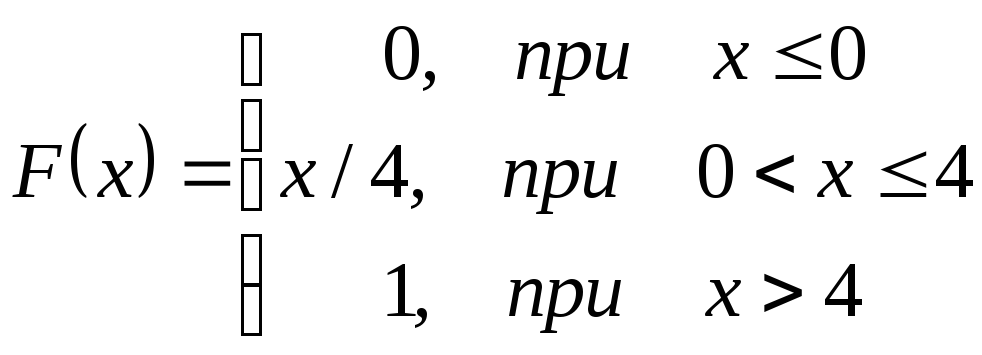
Ж: M (X) =1 / 8
![]() - қатарының
жинақты болуының қажетті шартын
көрсетіңіз
Ж: lim an
= 0
- қатарының
жинақты болуының қажетті шартын
көрсетіңіз
Ж: lim an
= 0
![]() қатарының жинақсыз болуының
жеткілікті шартын көрсетіңіз Ж:
lim an
= 0
қатарының жинақсыз болуының
жеткілікті шартын көрсетіңіз Ж:
lim an
= 0
![]() гармоникалық қатары қандай
болады?
гармоникалық қатары қандай
болады?
Ж: жинақсыз
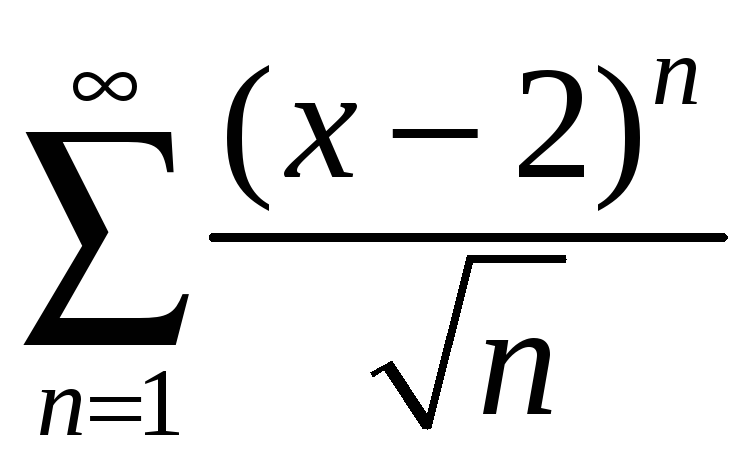 қатарының жинақтылық аймағын
табыңыз Ж: [ 1; 3)
қатарының жинақтылық аймағын
табыңыз Ж: [ 1; 3)
![]() қатарының қосындысын табыңыз
қатарының қосындысын табыңыз
Ж: 3
![]() қатарды жинақтылыққа зерттеңіз
Ж: жинақсыз
қатарды жинақтылыққа зерттеңіз
Ж: жинақсыз
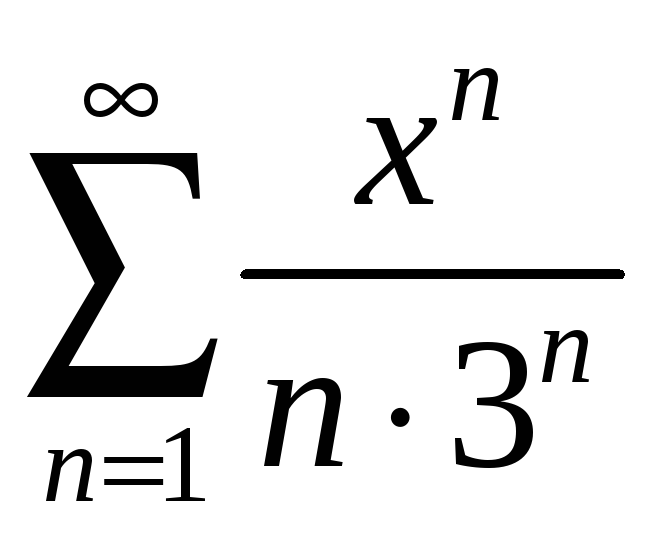 қатардың жинақтылық аймағын
табыңыз Ж: [ -3; 3)
қатардың жинақтылық аймағын
табыңыз Ж: [ -3; 3)
![]() қатардың жинақтылық аймағын
табыңыз Ж (-1; 5]
қатардың жинақтылық аймағын
табыңыз Ж (-1; 5]
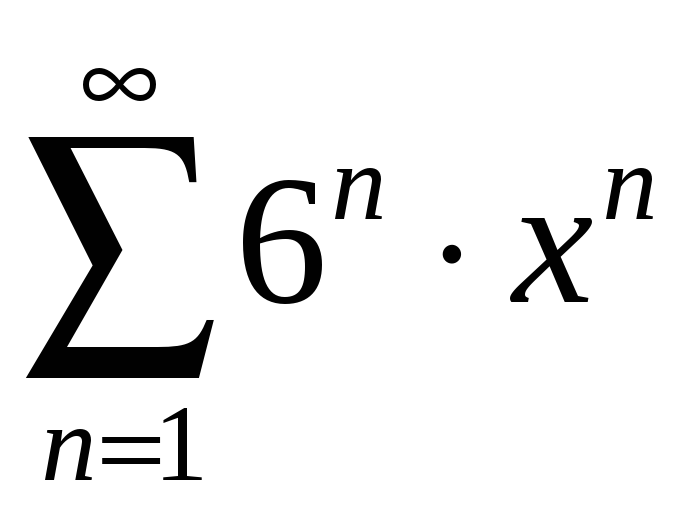 қатардың жинақтылық радиусын
табыңыз Ж: 1/6
қатардың жинақтылық радиусын
табыңыз Ж: 1/6
![]() қатардың жинақтылық радиусын
табыңыз Ж: +
қатардың жинақтылық радиусын
табыңыз Ж: +
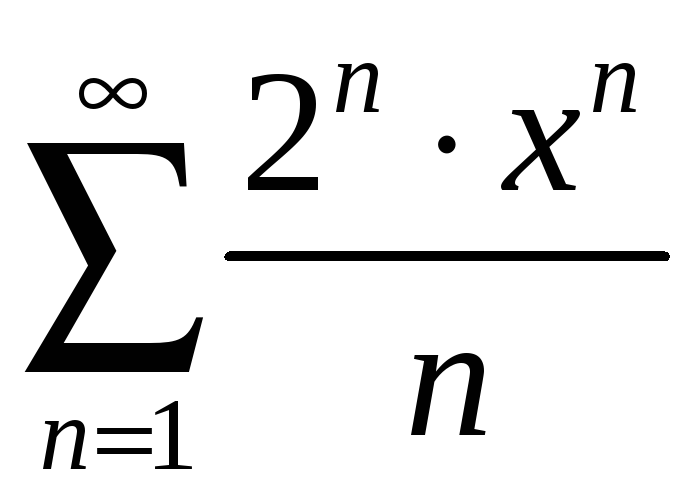 қатардың жинақтылық аймағын
табыңыз Ж: [-1/2; 1/2]
қатардың жинақтылық аймағын
табыңыз Ж: [-1/2; 1/2]
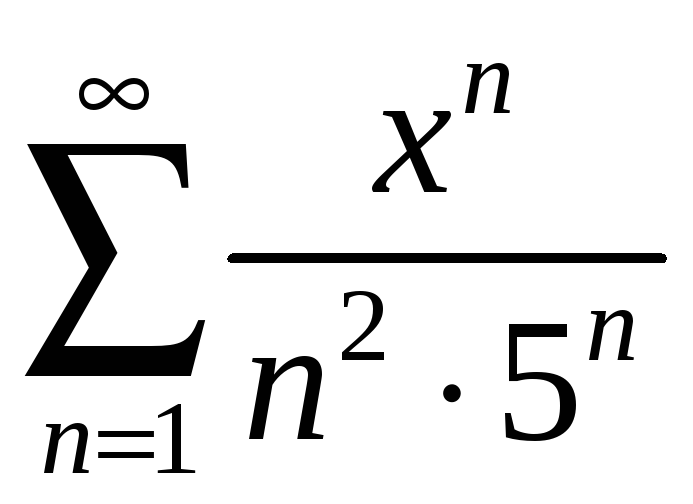 қатардың жинақтылық аймағын
табыңыз Ж: [-5; 5]
қатардың жинақтылық аймағын
табыңыз Ж: [-5; 5]
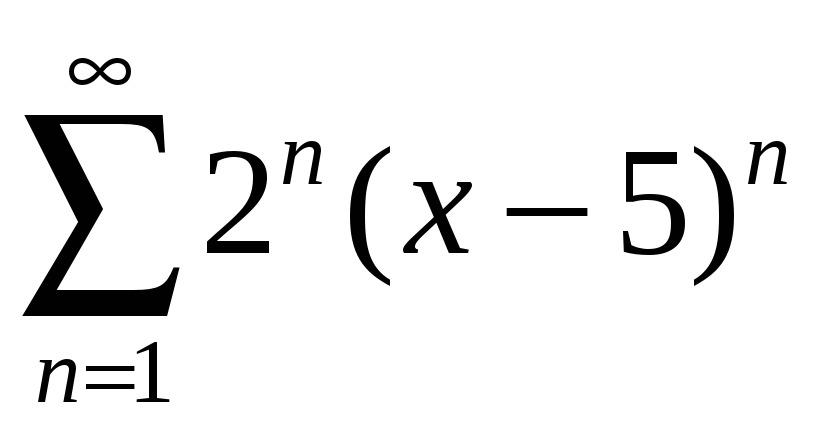 қатардың жинақтылық аймағын
табыңыз Ж (4,5; 5,5)
қатардың жинақтылық аймағын
табыңыз Ж (4,5; 5,5)
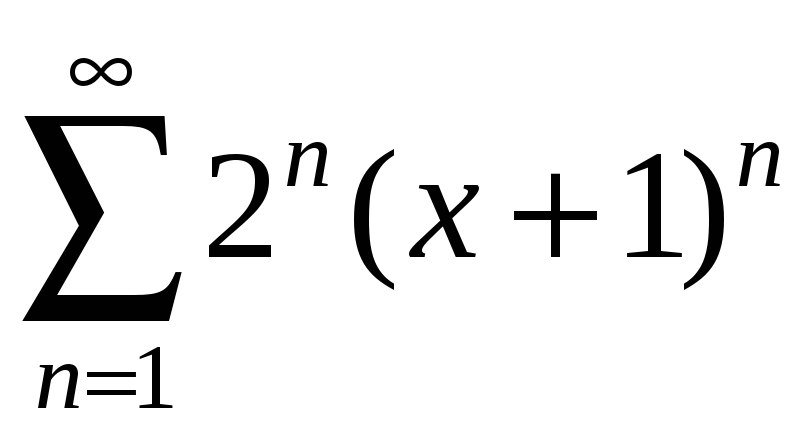 қатардың жинақтылық аймағын
табыңыз Ж: (-1,5; -0,5)
қатардың жинақтылық аймағын
табыңыз Ж: (-1,5; -0,5)
![]() қатарын жинақтылыққа зерттеңіз
Ж: жинақсыз
қатарын жинақтылыққа зерттеңіз
Ж: жинақсыз
![]() қатарын жинақтылыққа зерттеңіз
Ж: жинақсыз
қатарын жинақтылыққа зерттеңіз
Ж: жинақсыз
![]() қатарының жинақтылыққа
зерттеңіз Ж: жинақты
қатарының жинақтылыққа
зерттеңіз Ж: жинақты
![]() қатардың төртiншi мүшесiн
табыңыз Ж: 1/ 17
қатардың төртiншi мүшесiн
табыңыз Ж: 1/ 17
![]() қатардың төртiншi мүшесiн
табыңыз Ж: 1/ 16
қатардың төртiншi мүшесiн
табыңыз Ж: 1/ 16
![]() қатардың бесінші мүшесiн
табыңыз Ж: 10/ 13
қатардың бесінші мүшесiн
табыңыз Ж: 10/ 13
![]() қатарының алғашқы екі мүшесінің
қосындысын табыңыз Ж:
19/ 84
қатарының алғашқы екі мүшесінің
қосындысын табыңыз Ж:
19/ 84
![]() қатарының алғашқы екі мүшесінің
қосындысын табыңыз Ж:9/
8
қатарының алғашқы екі мүшесінің
қосындысын табыңыз Ж:9/
8
![]() қатарының алғашқы екі
мүшесінің қосындысын табыңыз
Ж:-3/ 70
қатарының алғашқы екі
мүшесінің қосындысын табыңыз
Ж:-3/ 70
![]() қатарының алғашқы екі
мүшесінің қосындысын табыңыз Ж:
-3/ 4
қатарының алғашқы екі
мүшесінің қосындысын табыңыз Ж:
-3/ 4
![]() қатарының үшінші және бесінші
мүшелерінің қосындысын табыңыз
қатарының үшінші және бесінші
мүшелерінің қосындысын табыңыз
Ж: -4/ 15
![]() қатарды
жинақтылыққа зерттеңіз
қатарды
жинақтылыққа зерттеңіз
Ж: абсолютті жинақты
![]() қатарды
жинақтылыққа зерттеңіз
қатарды
жинақтылыққа зерттеңіз
Ж: шартты жинақты
![]() қатардың жинақтылық радиусын
табыңыз Ж: 2
қатардың жинақтылық радиусын
табыңыз Ж: 2
![]() қатарын жинақтылыққа зерттеңіз
қатарын жинақтылыққа зерттеңіз
Ж: жинақты
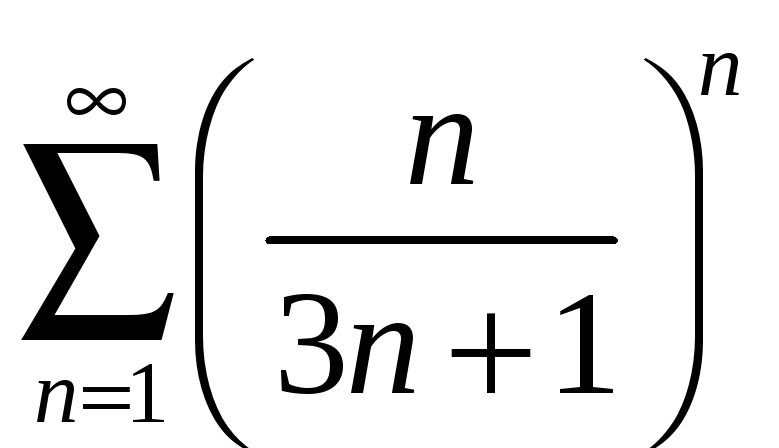 қатарды
жинақтылыққа зерттеңіз
қатарды
жинақтылыққа зерттеңіз
Ж: жинақты
![]() қатарды
жинақтылыққа зерттеңіз
қатарды
жинақтылыққа зерттеңіз
Ж: жинақты
![]() қатарын жинақтылыққа зерттеңіз
қатарын жинақтылыққа зерттеңіз
Ж:жинақты
![]() қатарын жинақтылыққа зерттеңіз
Ж: жинақсыз
қатарын жинақтылыққа зерттеңіз
Ж: жинақсыз
![]() қатарының жинақталу аралығын
табыңыз Ж: (-2, 2)
қатарының жинақталу аралығын
табыңыз Ж: (-2, 2)
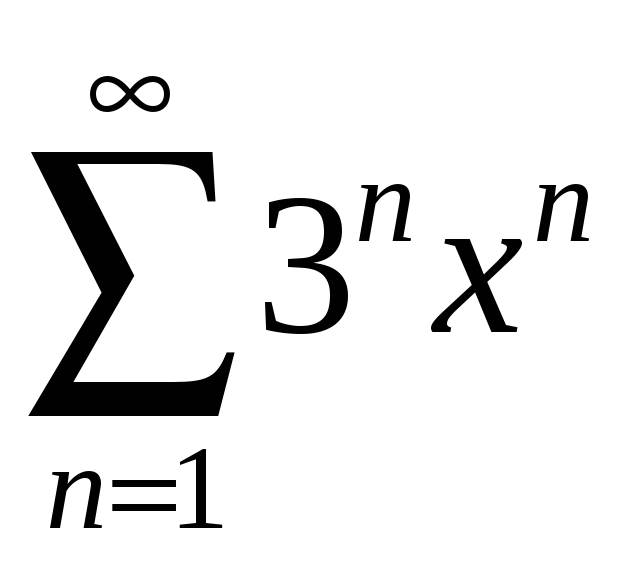 қатарының жинақталу радиусын
тап Ж: 1/3
қатарының жинақталу радиусын
тап Ж: 1/3
![]() қатарының жинақталу радиусын
тап
қатарының жинақталу радиусын
тап
Ж:5
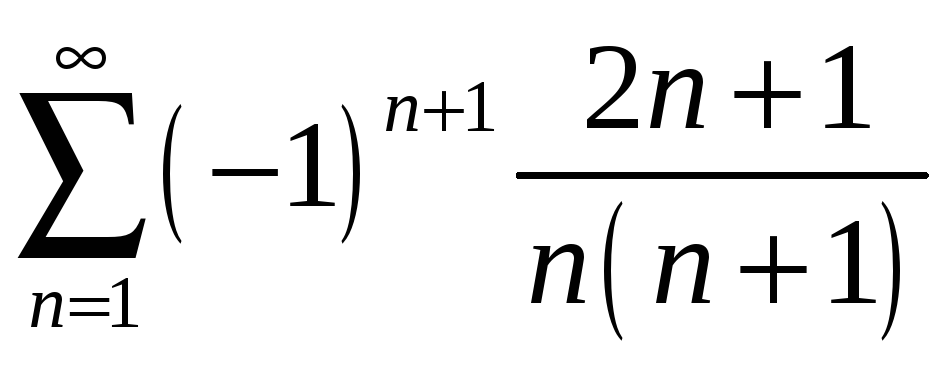 қатарының
қатарының
![]() және
және
![]() мүшелерінің қосындысын табыңыз
Ж: 2/15
мүшелерінің қосындысын табыңыз
Ж: 2/15
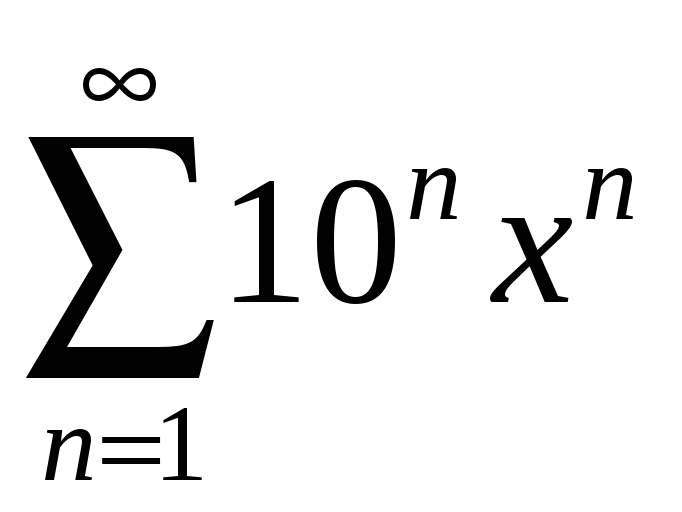 қатарының жинақталу интервалын
табыңыз Ж: (-1/ 10, 1/ 10)
қатарының жинақталу интервалын
табыңыз Ж: (-1/ 10, 1/ 10)
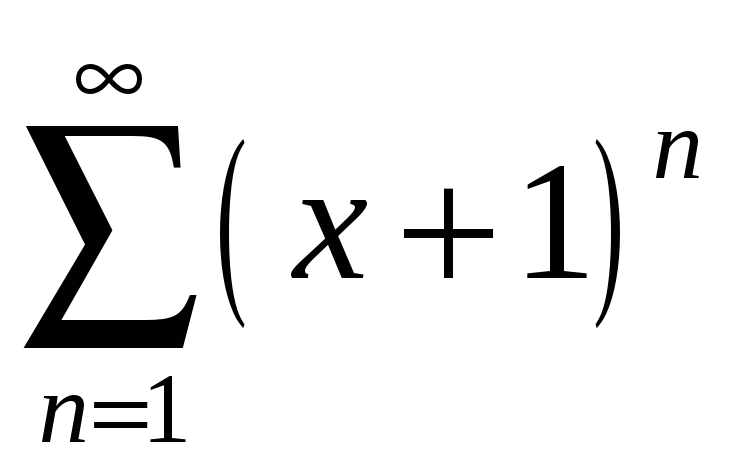 қатарының жинақталу интервалын
табыңыз Ж (-2, 0)
қатарының жинақталу интервалын
табыңыз Ж (-2, 0)
$$$ 371
 қатарының жинақталу интервалын
табыңыз Ж: (1 ,3)
қатарының жинақталу интервалын
табыңыз Ж: (1 ,3)
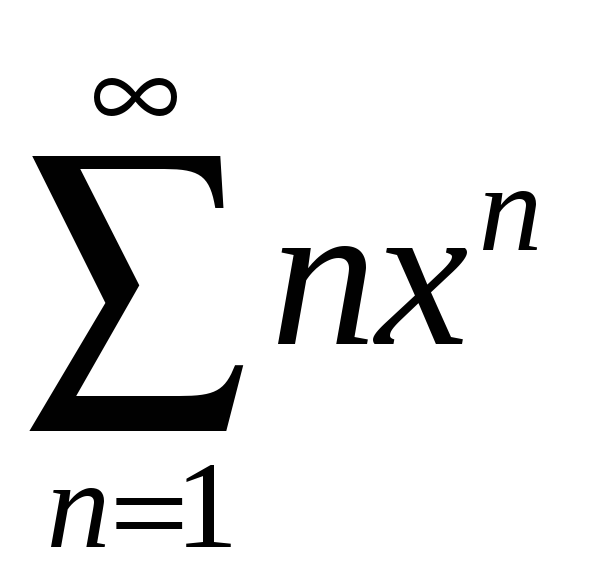 қатарының жинақталу интервалын
табыңыз Ж (-1, 1)
қатарының жинақталу интервалын
табыңыз Ж (-1, 1)
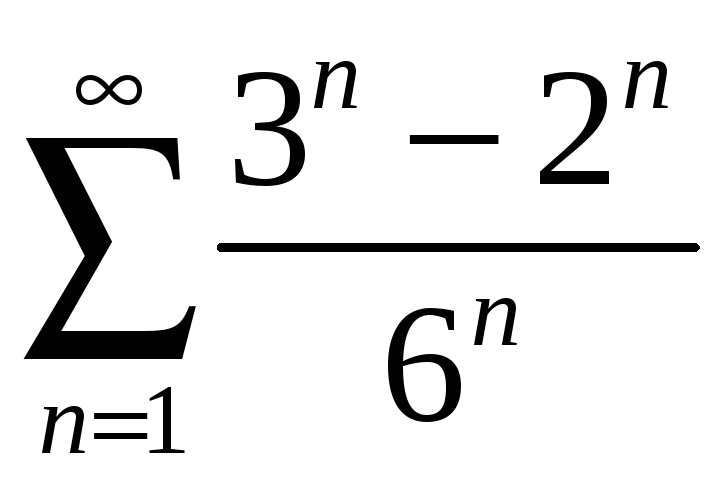 қатарының қосындысын табыңыз
Ж: 0,5
қатарының қосындысын табыңыз
Ж: 0,5
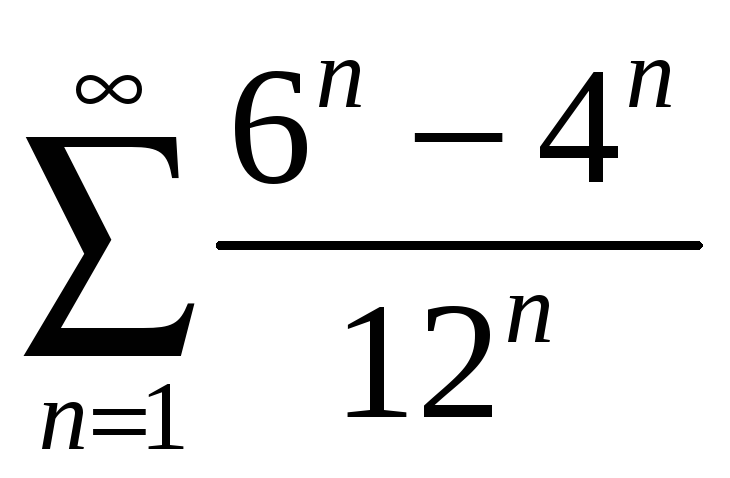 қатарының қосындысын табыңыз
Ж: 0,5
қатарының қосындысын табыңыз
Ж: 0,5
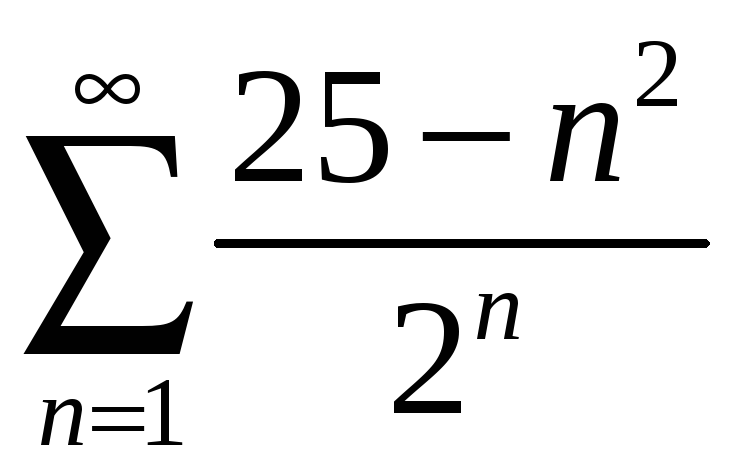 қатарының бірінші және үшінші мүшелерінің
айырымын табыңыз
қатарының бірінші және үшінші мүшелерінің
айырымын табыңыз
Ж: 10
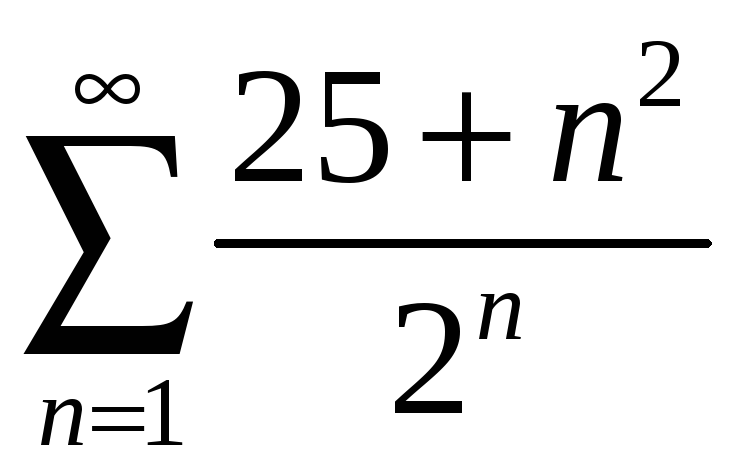 қатарының бірінші және үшінші мүшелерінің
қосындысын табыңыз
қатарының бірінші және үшінші мүшелерінің
қосындысын табыңыз
Ж: 17,25
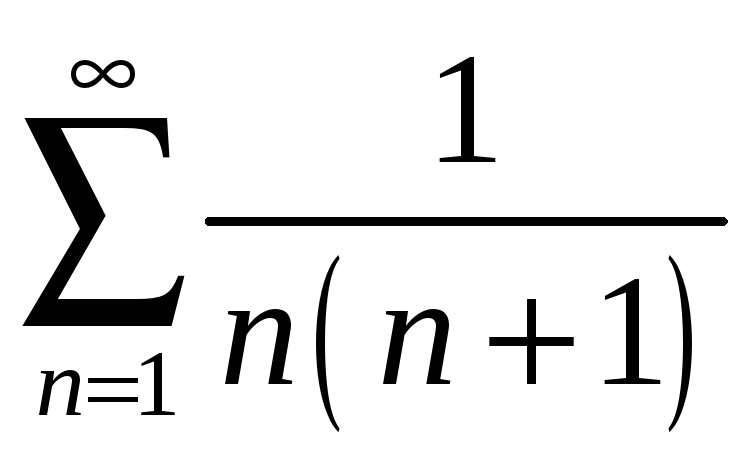 қатарының қосындысын табыңыз
Ж: 1
қатарының қосындысын табыңыз
Ж: 1
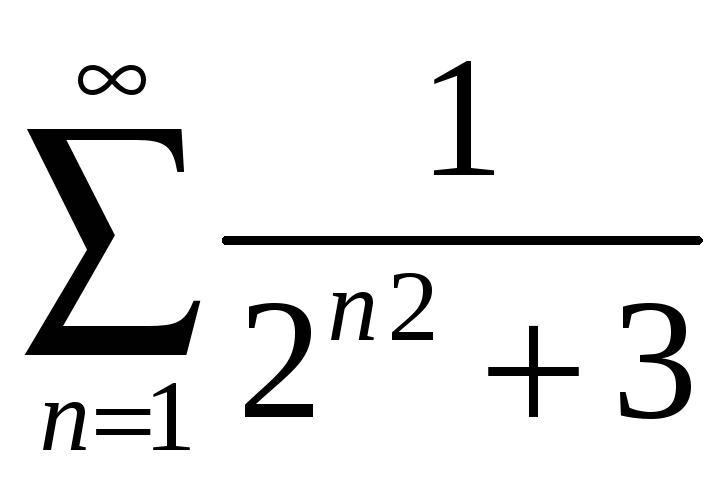 қатарының алғашқы екі мүшесінің
қосындысын табыңыз Ж:
16/ 55
қатарының алғашқы екі мүшесінің
қосындысын табыңыз Ж:
16/ 55
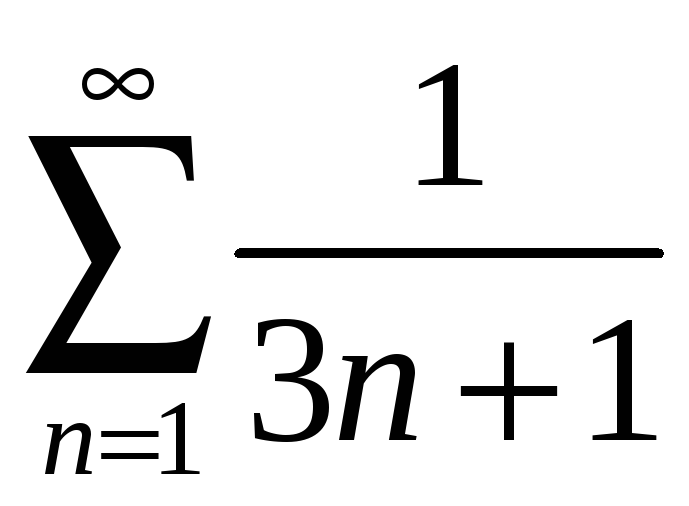 қатарының алғашқы үш мүшесінің
қосындысын табыңыз Ж:
69/ 140
қатарының алғашқы үш мүшесінің
қосындысын табыңыз Ж:
69/ 140
![]() дәрежелік қатардың жинақталу
радиусын табыңыз Ж:4
дәрежелік қатардың жинақталу
радиусын табыңыз Ж:4
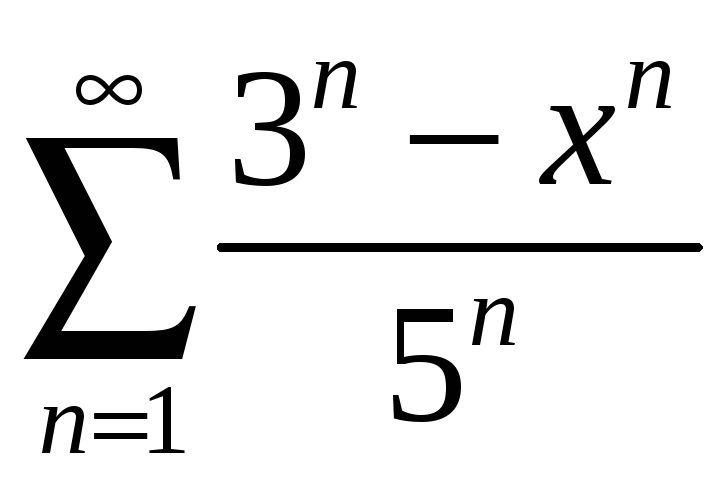 дәрежелік қатардың жинақталу
радиусын табыңыз Ж:5/ 3
дәрежелік қатардың жинақталу
радиусын табыңыз Ж:5/ 3
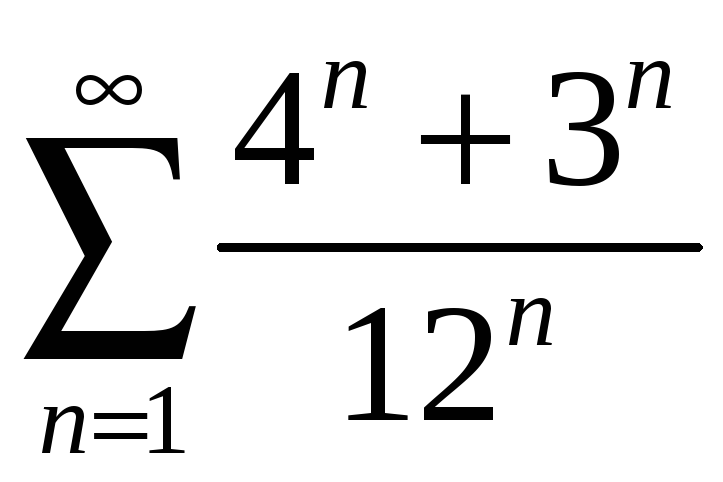 қатарының қосындысын табыңыз
Ж: 5/ 6
қатарының қосындысын табыңыз
Ж: 5/ 6
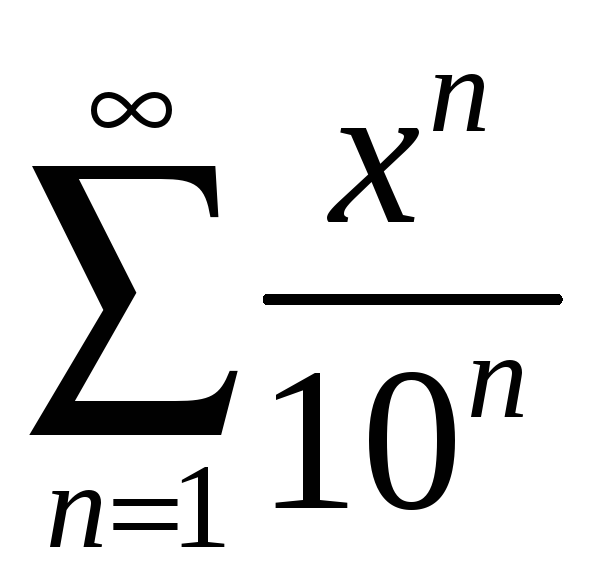 дәрежелік қатардың жинақталу
радиусын табыңыз Ж: 10
дәрежелік қатардың жинақталу
радиусын табыңыз Ж: 10
![]() және
және
![]() қатарлары жинақты, онда
қатарлары жинақты, онда
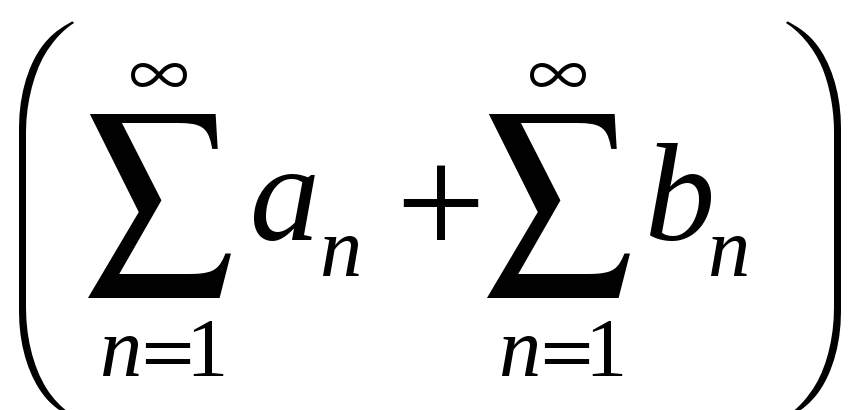 қатары туралы не айтуға болады
Ж: жинақты
қатары туралы не айтуға болады
Ж: жинақты
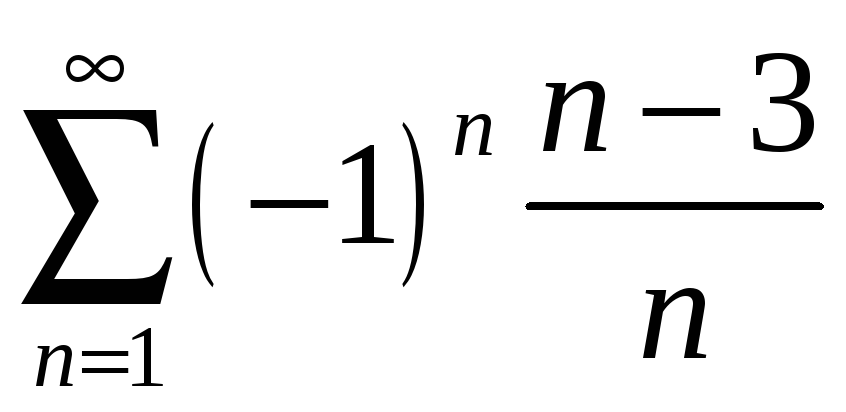 қатарының екінші және төртінші мүшелерінің
қосындысын табыңыз
қатарының екінші және төртінші мүшелерінің
қосындысын табыңыз
Ж: -1/ 4
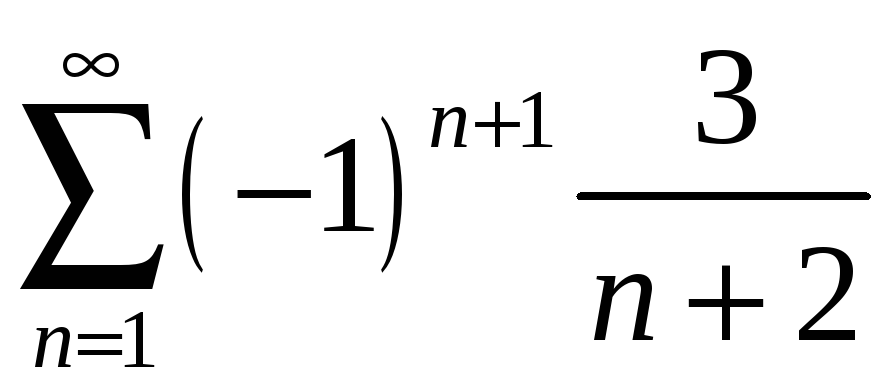 қатарының екінші және үшінші мүшелерінің
қосындысын табыңыз
қатарының екінші және үшінші мүшелерінің
қосындысын табыңыз
Ж: -3/ 20
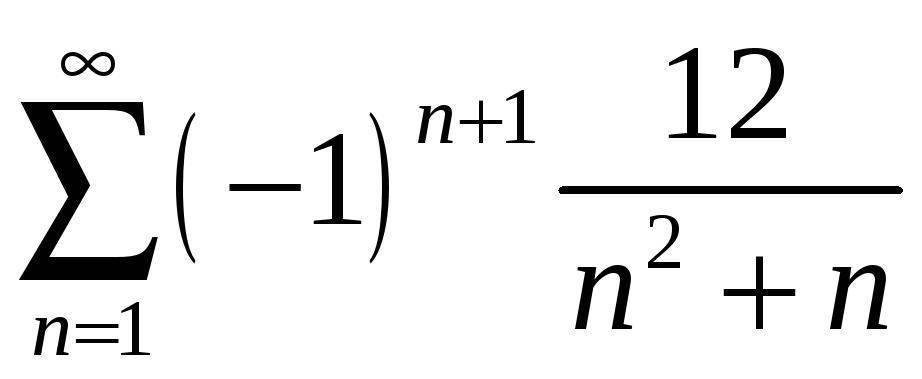 қатарының екінші және үшінші
мүшелерінің қосындысын табыңыз Ж:
-1
қатарының екінші және үшінші
мүшелерінің қосындысын табыңыз Ж:
-1
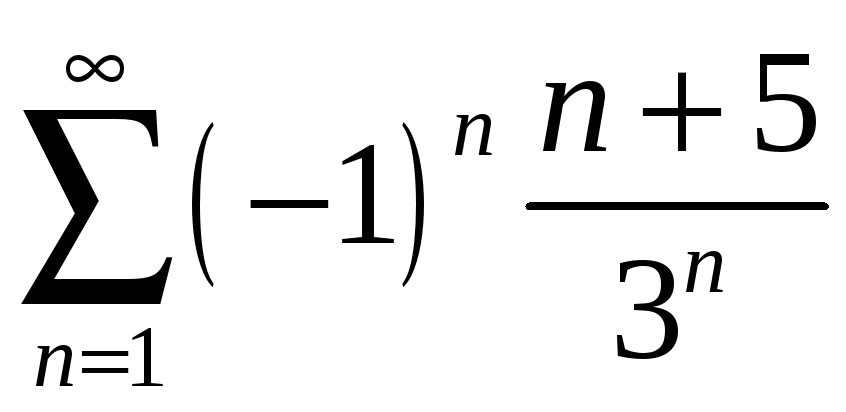 қатарының екінші және үшінші
мүшелерінің қосындысын табыңыз
Ж: 13/ 27
қатарының екінші және үшінші
мүшелерінің қосындысын табыңыз
Ж: 13/ 27
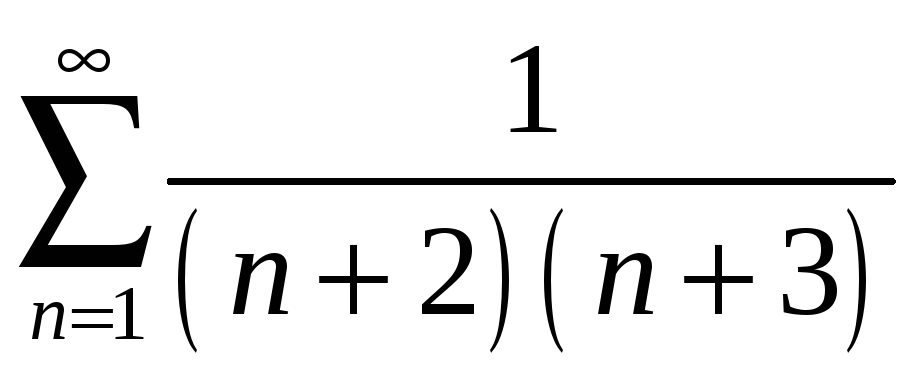 қатарының қосындысын табыңыз
Ж: 1/3
қатарының қосындысын табыңыз
Ж: 1/3
![]() қатарының қосындысын табыңыз
Ж: 1/ 4
қатарының қосындысын табыңыз
Ж: 1/ 4
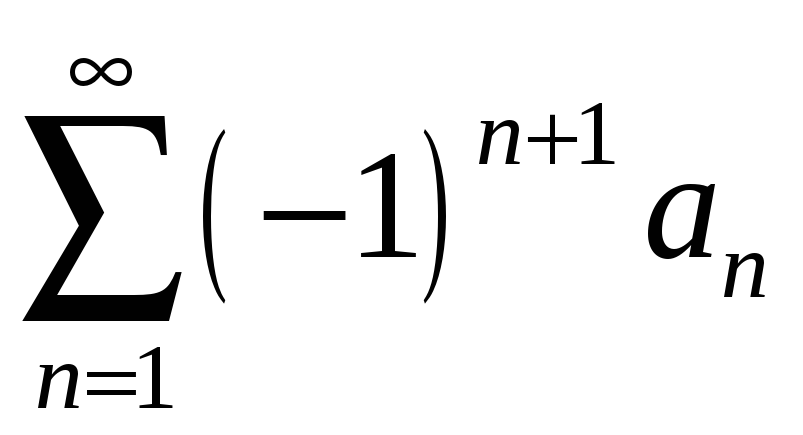 ауыспалы таңбалы қатары
жинақты және оның қосындысы
ауыспалы таңбалы қатары
жинақты және оның қосындысы
![]() -
ке тең болса, онда Ж: S <
|a1|
-
ке тең болса, онда Ж: S <
|a1|
Q(q)
![]() параметрінің қандай мәндерінде
параметрінің қандай мәндерінде
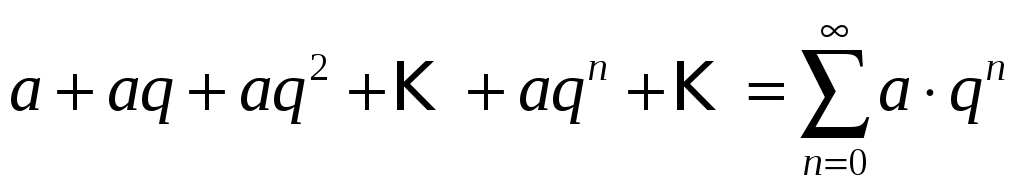 қатары жинақты? Ж: |q| <
1
қатары жинақты? Ж: |q| <
1
O(o)
Оқиғаның ықтималдығы тең болуы мүмкін:
Ж: [ 0, 1]
Ойын сүйегін бір рет лақтырғанда оның жоғарғы жағына тақ сандардың түсу ықтималдығын тап Ж: 1/ 2
Ойын сүйегін лақтырғанда оның жоғарғы жағына түскен санның 3-ке еселі болу ықтималдығын тап Ж: 1/ 3
K(k)
Кездейсоқ шаманың (а,в) аралығына түсу ықтималдығы дифференциалдық функция арқылы мына формуламен есептелінеді
Ж: P (a < X < b) = f (x) dx
Кездейсоқ шамамен тұрақты шаманың көбейтіндісінің дисперсиясы тең:
Ж: D (CX) = C2 D(X)
Карточкаларға жазылған М, Т, Р, О, Ш. әріптерін кездейсоқ бір қатарға араластырғанды «Шторм» деген сөздің жазылу ықтималдығын есептеңіз
Қ(қ)
Қатар жинақтылығының Коши белгісін көрсетіңіз Ж: lim = l < 1
Қатар жинақтылығының Даламбер белгісін көрсетіңіз
Ж: lim |an+1/ an|=l <1
Қатар жинақты деп аталады, егер
Ж: lim Sn = S (S-const)
Қарама-қарсы (![]() және
және![]() )
оқиғалардың ықтималдықтарының қосындысы
тең:
)
оқиғалардың ықтималдықтарының қосындысы
тең:
Ж: P (A) + P (A) =1
Қалыпты үлестіру заңдылықтың дифференциалдық функциясы мына түрде болады
Ж: f (x) = 1/ 5 2П e- (x-a) / 2П
Қалыпты үлестіру заңдылығымен
берілген Х кездейсоқ шаманың
дифференциалдық функциясы
![]() .
Кездейсоқ шаманың санды сипаттамалары
М(Х) және Д(Х) тең
.
Кездейсоқ шаманың санды сипаттамалары
М(Х) және Д(Х) тең
Ж: M (X) =1, D (X) =36
Қалыпты үлестіріммен берілген кездейсоқ шаманың берілген интервалдан мән қабылдауының ықтималдығын есептейтін формуласын көрсетіңіз:
Ж: < x < = Ф
Д(д)
Дәрежелік қатардың
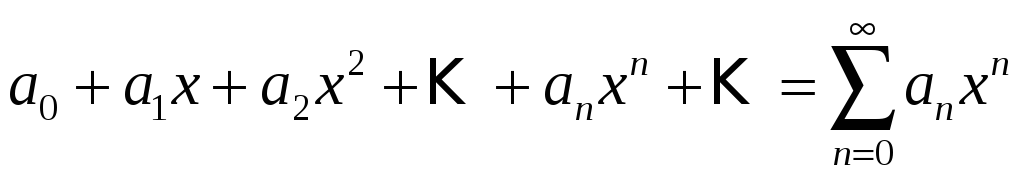 жинақтылық радиусын көрсетіңіз
жинақтылық радиусын көрсетіңіз
Ж: R=lim |an / an+1|
Дисперсия мына формуламен есептелінеді
Ж: D= x 2 – [x]2
Дисперсияны есептеу формуласын табыңыз
Ж: D = x2 - [x]2
Дискретті кездейсоқ шаманың математикалық үмітін көрсетіңіз
Ж: =x1p1 + x2p2 + … + xn pn
S(s)
![]() функциясының Маклорен қатарына
жіктелуін көрсетіңіз
функциясының Маклорен қатарына
жіктелуін көрсетіңіз
Ж:sinx = x-x3 / 3!+x5 / 5! -…+ (-1 )n-1 x2n-1 / (2n-1)! + …
C(c)
![]() функциясының Маклорен қатарына
жіктелуін көрсетіңіз
функциясының Маклорен қатарына
жіктелуін көрсетіңіз
Ж: cosx=1-x2/2! + x4/4!-…+(-1)n-1
x 2n-2 / (2n-2)!+…
Студенттің математикадан емтихан тапсыру ықтималдығы 0,5-ке, ал шет тілден емтихан тапсыру ықтималдығы - 0,6-ға тең. Оның ең кемінде бір емтихан тапсыру ықтималдығы неге тең?
Ж: 0,8
Студент 30 емтихан билеттерінің 18-ін жақсы оқып біліп алған. Ол кездейсоқ бір билетті алғанда оған жақсы біліп алған билеттің түсу ықтималдығы неге тең?
Ж: 3/ 5
Yү
Үзіліссіз кездейсоқ шаманың
интегралдық функциясы
![]() мына шарттардың қайсысын қанағаттандырады
мына шарттардың қайсысын қанағаттандырады
Ж: 0 < F (X) < 1
Үзіліссіз кездейсоқ шаманың (а,в) аралығына түсу ықтималдығы интегралдық функция арқылы мына формуламен есептелінеді
Ж: P (a < x < b) = F (b) – F (a)
N(n)
![]() -рет
тәуелсіз тәжірибелер жүргізгенде
-рет
тәуелсіз тәжірибелер жүргізгенде
![]() - оқиғасының пайда болу санының
математикалық үміті мына теңдікпен
анықталады
- оқиғасының пайда болу санының
математикалық үміті мына теңдікпен
анықталады
Ж: x) = np
ln
![]() функциясының дәрежелік
қатарға жіктелуін көрсетіңіз
функциясының дәрежелік
қатарға жіктелуін көрсетіңіз
Ж: x- x2 / 2 + x3 / 3 – x4 / 4+ (-1) n+1
xn / n + … x (-1, 1]
Бөлшек
![]() қатардың жалпы мүшесін табыңыз
қатардың жалпы мүшесін табыңыз
Ж: 2n-1 / 2n
![]() қатардың жалпы мүшесін табыңыз
қатардың жалпы мүшесін табыңыз
Ж: 2n/ 10n -1
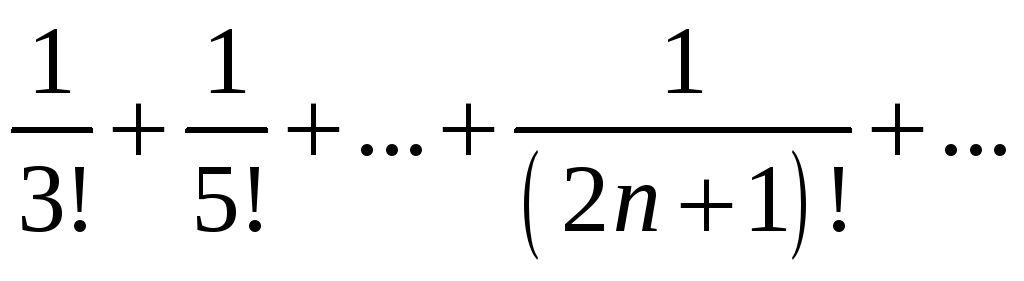 қатарының жинақтылыққа зертте
қатарының жинақтылыққа зертте
Ж: жинақты
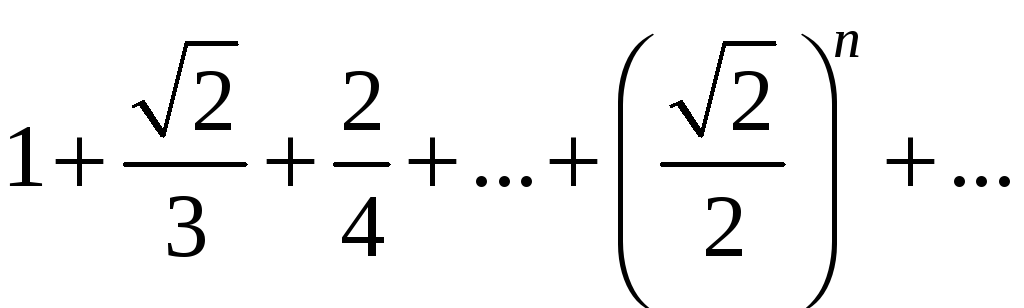 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Ж:жинақты
![]() қатарының жалпы мүшесін табыңыз
қатарының жалпы мүшесін табыңыз
Ж: 2n-1/ 3n+ 1
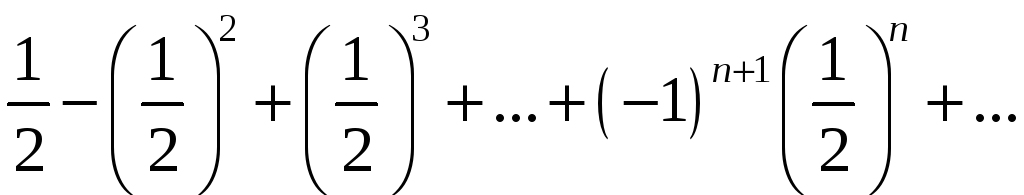 қатарының қосындысын табыңыз
қатарының қосындысын табыңыз
Ж: 1/ 3
![]() қатарының жалпы мүшесін табыңыз
қатарының жалпы мүшесін табыңыз
Ж: 2n-1/ 3n+1
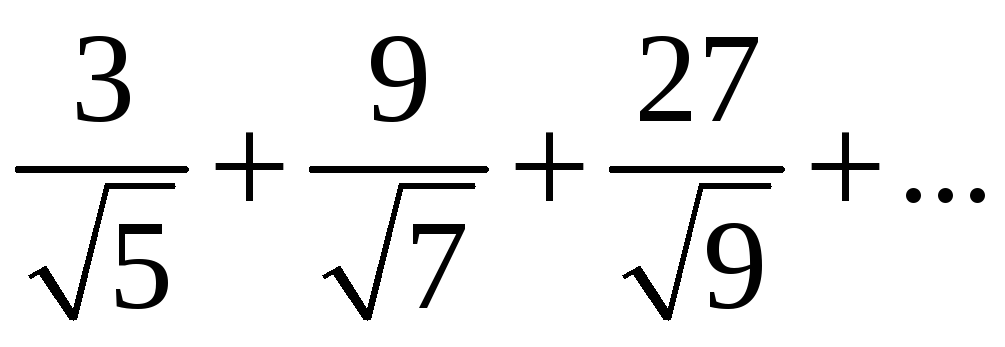 қатарының жалпы мүшесін табыңыз
қатарының жалпы мүшесін табыңыз
Ж: 3n / 2n+3
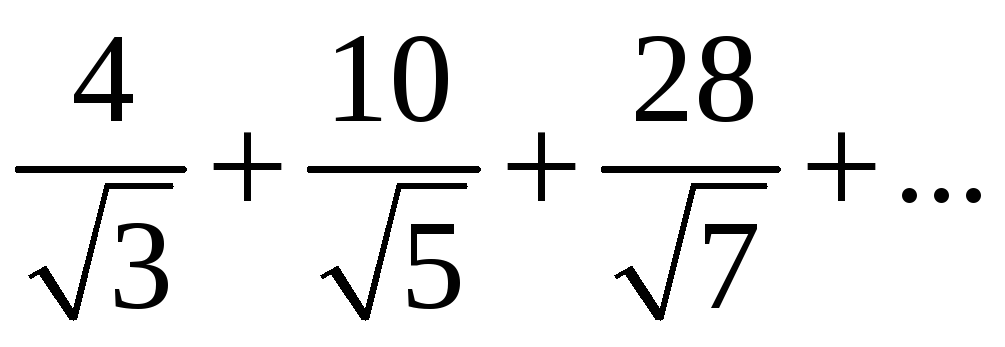 қатарының жалпы мүшесін табыңыз
қатарының жалпы мүшесін табыңыз
Ж: 3n +1 / 2n+3
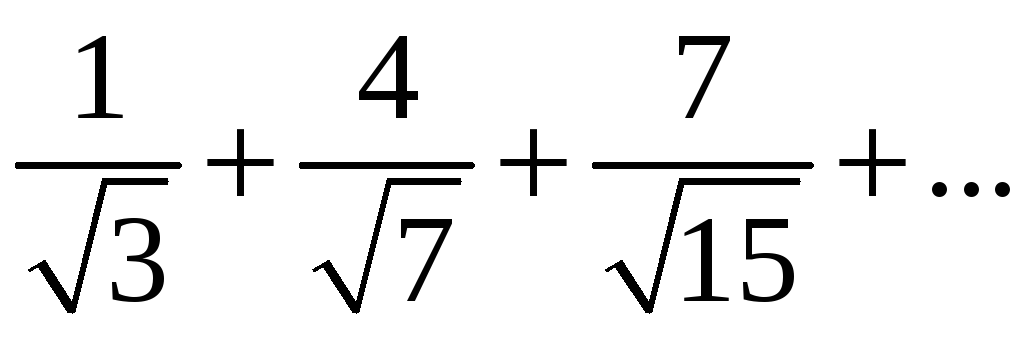 қатарының жалпы мүшесін табыңыз
қатарының жалпы мүшесін табыңыз
Ж: 3n - 2/ 2n+1 -1
