МЕХАНИКА

§ 1. Кинематика

Жалпы жағдайда түзу сызықты қозғалыстың жылдамдығы

Үдеуі

Түзу сызықты бір қалыпты қозғалыс болғaн жағдайда υ = const және = 0.

Түзу сызықты бір қалыпты айнымалы қозғалыс кезінде

, ,= const.

Бұл теңдеулерде үдеу бір қалыпты үдемелі қозғалыс кезінде оң болады да, ал бір қалыпты баяу қозғалыс кезінде теріс болады.

Қисық сызықты қозғалыс кезінде толық үдеу ,

мұндағы _t — тангенциал үдеу, ал — нормаль (центрге тартқыш үдеу) үдеу, сондықтан

_t,

мұндағы υ - қозғалыстың жылдамдығы, ал R — берілген нүктедегі траекторияның қисықтық радиусы.

Айналмалы қозғалыста жалпы жағдайында бұрыштық жылдамдық

ал бұрыштық үдеу

Бip қалыпты айналмалы қозғалыс кезінде бұрыштық жылдамдық ,

мұндағы Т - айналу периоды, ν — айналу жиілігі, яғни (бірлік уақыт ішіндегі айналым саны)

Бұрыштық жылдамдықтың сызықтық жылдамдықпен өз ара байланысы мына қатынаспен анықталады:

Тангенциал және нормаль үдеулер айналмалы қозғалыста мынадай түрде көрсетілуі мүмкін: ,

(6 - кестеде ілгерілемелі қозғалыс теңдеуінің айналмалы қозғалыс теңдеуімен салыстырмасы берілген.

6 – кесте

Ілгерілемелі қозғалыс	Айналмалы қозғалыс
Бір қалыпты
a=0	ε=0
Бір қалыпты айнымалы
а=соnst	ε=соnst
Бір қалыпсыз
s=f(t)	φ=f(t)

§ 2. Динамика

Динамиканың негізгі заңы (Ньютонның екінші заңы) мына теңдеумен өрнектеледі:

F dt = d(mυ).

Егер масса тұрақты болса, онда ,

Мұндағы а — F күштің әсерінен массасы m дененің алатын үдеуі.

F күштің s орын ауыстырғандағы жұмысы мынадай формуламен өрнектелуі мүмкін:

мұндағы F_s — жол бағытындағы күштің проекциясы, ds — жол учаскесінің шамасы. Иптегралдау s жолына тұтас таралуға тиіс. Кей жағдайда орын ауыстыруға тұрақты бұрыш жасай әсер ететін тұрақты күшке мынаны аламыз: ,

мұндағы— F күш пен s жүрген жол арасындағы бұрыш.

Қуат төмендегі формуламен анықталады: .

Тұрақты қуат жағдайында ,

мұндағы А — t уақыт ішіндегі істеліпетін жұмыс.

Сондай-ақ қуатты мынадай формуламен анықтауға болады: N = Fυ cos a,

яғни қуат қозғалыс жылдамдығының қозғалыс бағытындағы күш проекциясының көбейтіндісімен анықталады.

V жылдамдықпен қозғалатын, массасы т дененің кинетикалық энергиясы мынаған тең: .

Әсер етуші күштің сипатына қарай, потенциалық энсргияның формуласы әр түрлі болады.

Изоляцияланған системада оған енетін барлық денелердің қозғалыс мөлшері тұрақты болып қалады, яғни .

Массалары т₁ және m₂ екі денепің серпімсіз центрлік соғылысқан кезде осы денелердің соғылысқаннан кейінгі қозғалысының жалпы жылдамдығын төмендегі формуламен табуға болады: .

мұндағы — соғылғанға дейінгі бірінші дененің жылдамдығы, ал — соғылғанға дейінгі екінші дененің жылдамдығы.

Денелер серпімді центрлік соғылысқан кезде әр түрлі жылдамдықпен қозғалатын болады. Соғылысқаннан кейінгі бірінші дененің жылдамдығы ,

соғылысқаннан кейінгі екінші дененің жылдамдығы .

Қисық сызықты қозғалыста материялық нүктеге әсер ететін күшті екі құраушы күшке жіктеуге болады: тангенциаль және нормаль күштерге.

Нормаль құраушы

центрге тартқыш күш болады. Мұнда υ — массасы т дененің қозғалысының сызықтық жылдамдығы, R — берілген пүктедегі траекторияның қисықтық радиусы.

Серпімді деформация х туғызатын күш деформацияның шамасына пропорционал, яғни F = kx,

мұндағы k — бірге тең деформация туғызатын, сан жағынан күшке тең коэффицент (деформация коэффициенті).

Серпімді күштің потенциал энергиясы

Екі материялық нүкте (яғни өлшемдері олардың өз ара қашықтықтарына қарағанда кішкене больп келетін денелер) бір-біріне мынадай күшпен тартылады: ,

мұндағы тартылыс тұрақтысы немесе гравитациялық тұрақты, бұл тең = 6,67 • 10^-11 м³/кг • сек²,т₁ және т₂ — өз ара әсер ететін материялық нүктелердің массасы; R— олардың ара қашықтығы. Бұл заңды біртекті шарларға да қолдануға болады. Сонда R — олардың центрлерінің ара қашықтығы болады.

Тартылыс күшінің потенциалық энергиясы

«Минус» таңбасы R— болғандағы өз ара әсер етуші екі денелердің потенциалық эпергиясының нолге тең болатындығын көрсетеді, ал бұл денелер бір-біріне жақындағанда потенциал энергия кемиді.

Кеплердің үшінші заңы мына түрде болады:

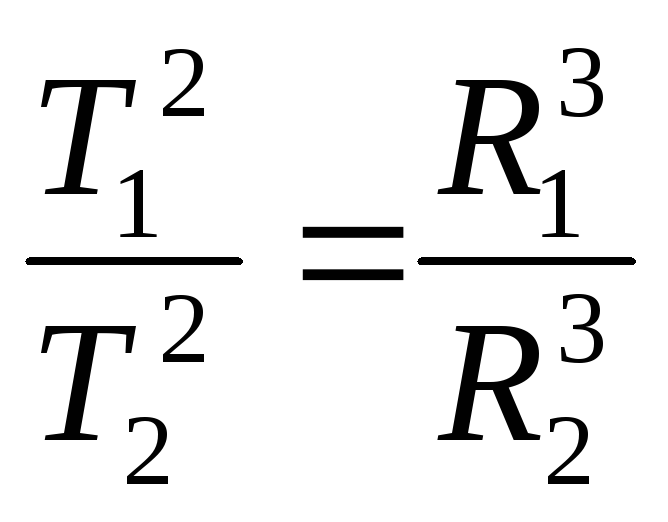
мұндағы Т₁ және Т₂ — планеталардың айналып шығу пе­риоды, R₁ жәпе R₂ — олардың орбиталарының үлкен жар­ты остері. Дөңгелек орбита жағдайында үлкен жарты осьтің ролін орбита радиусы атқарады.