14.1.2.2. Многократная дистилляция

Процесс многократной дистилляции рассмотрим на примере двукратной (рис. 14.10). В этом случае кубовый остаток, полученный при однократной дистилляции, вновь подвергается ей повторно. Уравнения, аналогичные (14.15) (14.21), записываются для каждой ступени однократного испарения, при этом номер ступени указывается индексомi, которым снабжаются все величины.

Поскольку после каждой ступени в жидкой смеси, подвергаемой дистилляции, доля легколетучего компонента будет уменьшаться, то уменьшаться его доля будет в кубовом остатке и в дистилляте (рис. 14.11): x_F,2<x_F,1, x_W,2<x_W,1, x_D,2<x_D,1.

Рис. 14.10. Схема установки непрерывной двукратной дистилляции: 1 испарители; 2сепараторы; 3конденсаторы

Рис. 14.11. Изображение двукратной дистилляции на Тxy диаграмме

При увеличении числа ступеней (кратности дистилляции) можно получить кубовый остаток, состоящий из практически чистого труднолетучего компонента. Однако его количество будет невелико, так как с каждой ступенью величина будет уменьшаться, определяясь долей отгона на каждой ступениe_i.

. (14.22)

14.1.2.3. Постепенная дистилляция

Процесс постепенной дистилляции проводится периодическим способом. Исходную смесь количеством F кмоль загружают в куб-испаритель 1 (рис. 14.12), нагревают до температуры кипения и постепенно испаряют. Пары по мере образования поступают в конденсатор 2, полностью конденсируются и образовавшаяся жидкость собирается в сборнике дистиллята 3. С течением времени кубовая жидкость и, соответственно, равновесные с ней пары, а также образующийся дистиллят обедняются легколетучим компонентом (рис. 14.13).

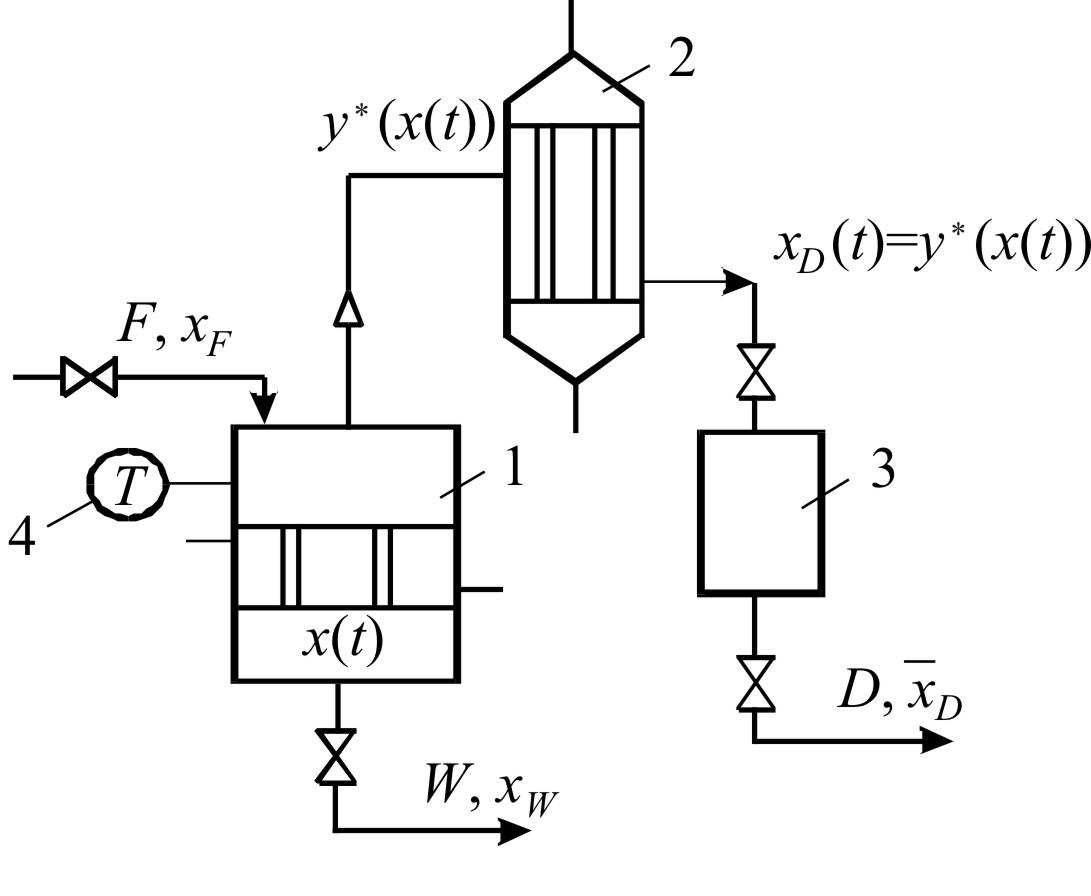
Рис. 14.12. Схема установки постепенной дистилляции: 1 куб-испаритель; 2конденсатор; 3сборник дистиллята; 4измеритель температуры.

Процесс заканчивается по истечении времени t_п при достижении заданного состава кубового остатка x_W или среднего состава дистиллята . Следить за изменением состава куба достаточно просто по температуре в нем, пользуясьTxy диаграммой (рис. 14.13). Полученные продукты сливаются из куба и сборника дистиллята, затем процесс возобновляется.

Запишем в дифференциальной форме уравнение материального баланса для текущего момента времени t по легколетучему компоненту. Его количество в кубовой жидкости L состава x за бесконечно малый промежуток времени dt уменьшится на d(Lx). Такое же количество легколетучего компонента, которое можно записать как y^(x)dL, должно перейти в пар.

. (14.23)

Разделив переменные и проинтегрировав, получим

, (14.24)

. (14.25)

В общем случае интеграл в правой части уравнения (14.25) находится аналитически, если зависимость y^(x) это позволяет, либо численно. В случае, если коэффициент относительной летучести  можно считать в диапазоне от x_W до x_F неизменным, подставляя вместо y^(x) (14.7) в (14.25) и интегрируя, найдем

. (14.26)

Можно записать уравнения материального баланса по смеси в целом и по легколетучему компоненту в интегральной форме, характеризующие результаты процесса постепенной дистилляции:

, (14.27)

. (14.28)

Система уравнений (14.25) или (14.26), а также (14.27) и (14.28) позволяет найти при известных F, x_F и заданном x_W все остальные величины: W, D, . В зависимости от поставленной задачи наборы заданных и искомых величин могут меняться.

Рис. 14.13. Изменение составов куба и дистиллята, а также температуры процесса постепенной дистилляции со временем