10330

[Введите текст]

Лекция 4. Системы m уравнений с n неизвестными

4.1. Ранг матрицы. Мы рассматривали систему n уравнений с n неизвестными, у которой матрица невырожденная. А как быть, если матрица вырожденная ( ( A) 0) или m n , то есть число неизвестных не совпадает

с числом уравнений?

Для того чтобы ответить на этот вопрос, нам понадобится понятие ранга матрицы. Это некоторая числовая характеристика матрицы. Вводится она следующим образом. Выберем некоторые k строк и k столбцов и образуем матрицу порядка k , которая состоит из элементов, стоящих на их пересечении. Определитель этой матрицы будем называть минором k -го порядка.

Рангом матрицы A называется число r( A) , равное наибольшему из

порядков её миноров, отличных от нуля. Если все миноры равны нулю, что возможно только для нулевой матрицы, то r 0 .

Очевидно, что ранг — это число, удовлетворяющее неравенству

0 r min m,n ,

где m и n – размеры матрицы. Например,

так как все миноры второго порядка равны нулю.

Если матрица квадратная и невырожденная, то её ранг равен порядку матрицы.

Один из способов вычисления ранга – это «идти снизу», последовательно находя неравные нулю миноры первого, второго и следующих порядков.

4.2. Теорема Кронекера-Капелли. Выше при рассмотрении системы линейных уравнений мы ограничивались случаем, когда число уравнений совпадало с числом неизвестных и когда матрица системы была невырожденной. В этом случае система имеет единственное решение. Сейчас мы рассмотрим общий случай системы m уравнений с n неизвестными

30

[Введите текст]

Образуем так называемую «расширенную» матрицу B , полученную присоединением к матрице A столбца из свободных членов уравнений системы

Очевидно, что rang A rang B .

Вопрос о совместности системы решает теорема Кронекера-Капелли (Леопольд Крóнекер (1823-1891г.г.) – немецкий математик и Альфредо Капелли (1855-1910 г.г.) – итальянский математик).

Теорема Кронекера-Кaпелли. Система линейных уравнений (4.1) совместна тогда и только тогда, когда

rang A rang B

(принимаем без доказательства).

Проиллюстрируем эту теорему в случае системы трех уравнений с тремя неизвестными

Если det A 0 , то rang B rang A 3 и, следовательно, система совместна. Если det A 0 и существует отличный от нуля определитель третьего по-

[Введите текст]

значит, система несовместна. И, наконец, если x y z 0 , то

rang B 3, rang A 3 и, следовательно, в соответствии с теоремой Кро-

некера-Капелли система будет совместна тогда и только тогда, когда выполняется условие

rang A rang B .

так как ранг не может быть больше числа строк. Система совместна. Найдите её единственное решение.

(проверьте!), но есть минор второго порядка, отличный от нуля. Из расширенной матрицы образуем минор

(проверьте!). Значит, rang B 3 и, следовательно, эта система несовместна.

Из теоремы Кронекера-Капелли следует, что система n уравнений с n неизвестными с отличным от нуля определителем всегда совместна. Её единственное решение можно получить по правилу Крамера. В частности, однородная система уравнений, у которой все правые части равны нулю, а определитель не равен нулю, имеет единственное так называемое тривиальное решение.

Совместная система m уравнений с n неизвестными обладает единственным решением тогда и только тогда, когда ранг матрицы системы равен числу неизвестных. Поясним это на следующем примере.

[Введите текст]

поэтому rang A 3. Вычислим минор четвёртого порядка расширенной матрицы B

(сложим третий столбец последовательно с первым, вторым столбцами)

(вычитая из первого столбца третий, получим)

значит, rang B 3. Система совместна и число неизвестных совпадает с ран-

гом. Как найти ее решения? Нужно выписать те уравнения системы, которые дают отличный от нуля минор третьего порядка (так называемый базисный минор). В данном случае это три первых уравнения. Проверьте, что единственным решением системы этих уравнений будет (1, 2, 3) и оно удовлетворяет и оставшемуся уравнению. Это следует из того, что определитель расширенной матрицы равен нулю и, следовательно, элементы ее четвертой строки являются линейными комбинациями соответствующих элементов первых трех строк (см. свойство 9 определителей).

Из расширенной матрицы можно составить три минора третьего порядка (столбец свободных членов последовательно подставляется вместо коэффициентов при неизвестных). Убедитесь, что все они равны нулю. Значит,

rang B 2 . Система совместна, но ранг матрицы A меньше числа неизвест-

ных, поэтому система имеет бесчисленное множество решений. Как их найти? Выписываем уравнения, «дающие» базисный минор, оставляя в левой

33

[Введите текст]

части число неизвестных, равное рангу матрицы (причём оставляем те неизвестные, которые «входят» в базисный минор)

x 2 y z 3x 3y 1 z

Решаем эту систему, считая z произвольным параметром

Сформулируем теперь общее правило, по которому решается совместная система линейных уравнений. Пусть rang A= r .

Отыскиваем базисный минор порядка r (он получается при нахождении ранга матрицы).

Выбираем r уравнений, «породивших» базисный минор (остальные отбрасываем).

Неизвестные, «входящие» в базисный минор, оставляем слева, а остальные n r называем свободными и переносим в правые части уравнений.

Решаем полученную систему r уравнений r с неизвестными. Из этого правила следует, что в случае, когда ранг совместной системы

меньше, чем число неизвестных, то эта система имеет бесконечно много решений. В частности, однородная система n уравнений с n неизвестными и равным нулю определителем, т.е. когда

rang A rang B n ,

кроме тривиального имеет ненулевые решения.

34

[Введите текст]

Раздел 2. Векторная алгебра

Лекция 5. Векторы и линейные операции над ними

5.1. Основные понятия и определения. Понятие вектора сформиро-

валось в физике, точнее в механике. Скорость, ускорение, сила определяются величиной и направлением и называются векторными величинами. Масса, объем, температура и т.п. определяются численным значением и называются скалярами или скалярными величинами. Вектор – это направ-

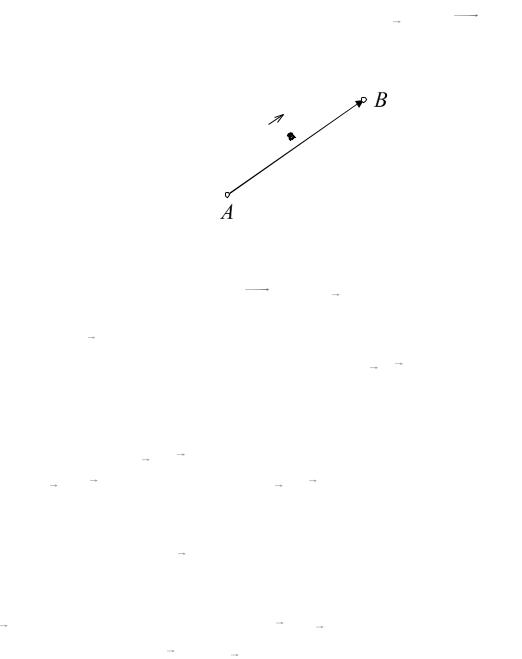
ленный отрезок. Обозначается вектор символом a или AB , где точка A

– начало, а B – конец.

Рис 5.1.

Длиной или модулем вектора называется расстояние между его нача-

лом и концом и обозначается | AB | или | a |.

Если начало и конец вектора совпадают, то он называется нулевым вектором 0 .

Векторы называются коллинеарными a || b , если они параллельны одной прямой.

Векторы называются компланарными, если они параллельны одной плоскости (очевидно, что любые два вектора компланарны).

Два вектора a и b равны, если они коллинеарны , одинаково направ-

щении вектора параллельно самому себе получим равный ему вектор. Единичным вектором или ортом называется вектор, модуль кото-

рого равен единице | a | 1 .

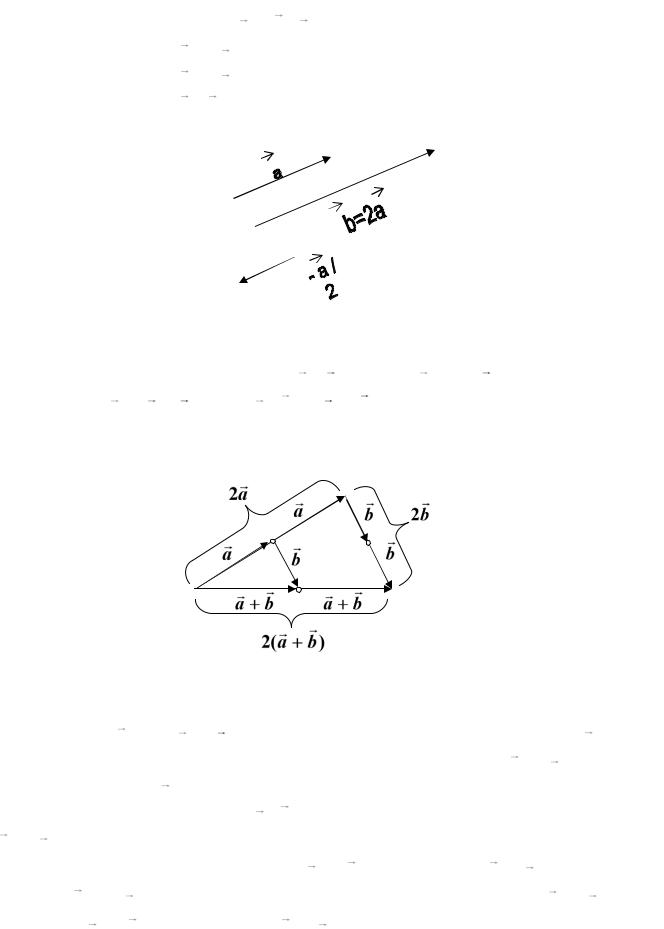
5.2. Линейные операции над векторами. Произведением вектора a на число k называется вектор b k a , который:

имеет длину | b | | k | |a |

35

Рис. 5.3

Вектор b ( 1) a a называется противоположным вектору a . По определению операции умножения вектора на число вектор b k a коллинеарен вектору a . Покажем, что имеет место обратное утверждение: если два вектора коллинеарны ( a || b ), то существует такое число k 0 , что b k a , и это число с точностью до знака равно отношению длин этих векторов. Действительно, в случае, если a b , возьмем k | b | / | a | . Тогда векторы b и k a направлены в одну сторону и их длины равны, т.е. b k a

. В случае a b выберем k | b | / | a |.

36

[Введите текст]

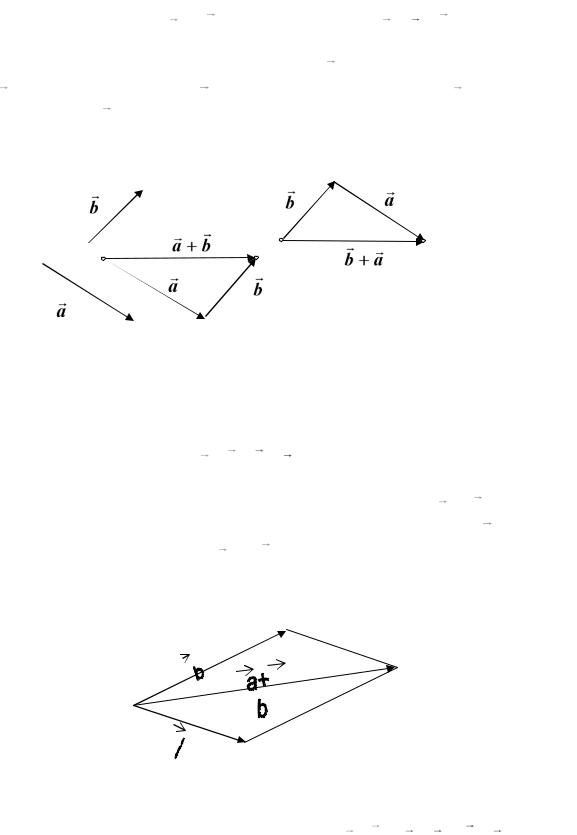
Суммой двух векторов a и b называется вектор c a b , получаемый по одному из следующих правил.

Правило треугольника: начало вектора b совмещается с концом вектора a , тогда начало вектора c совпадает с началом вектора a , а конец

– с концом вектора b (рис 5.4).

Рис. 5.4

Из рисунка ясно, что порядок слагаемых может быть любой, т.е.

a b b a .

Отсюда следует правило параллелограмма: на векторах a и b , имеющих общее начало, строится параллелограмм, тогда начало вектора c сов-

падает с общим началом векторов a и b , а конец – с противоположной вершиной параллелограмма (рис. 5.5).

Рис. 5.5

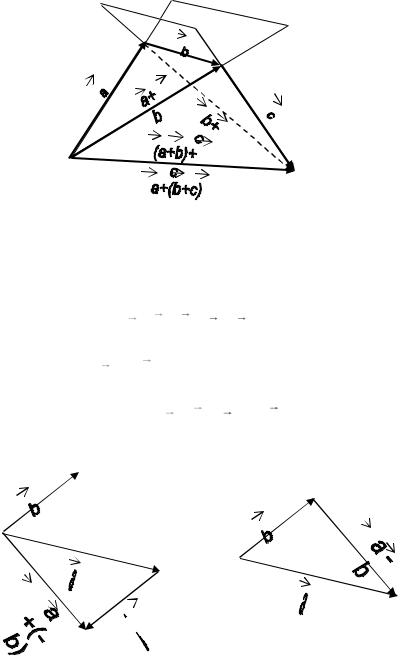
Для суммы справедлив сочетательный закон (a b) c a (b c ) .

Заметим, что векторы не обязаны быть расположенными в одной плоскости (см. рис. 5.6).

37

[Введите текст]

Рис. 5.6

Отметим также операцию сложения с нуль-вектором

a 0 0 a a

Разность векторов a и b определяется через введенные выше операции следующим образом

a b a ( b)

Рис. 5.7

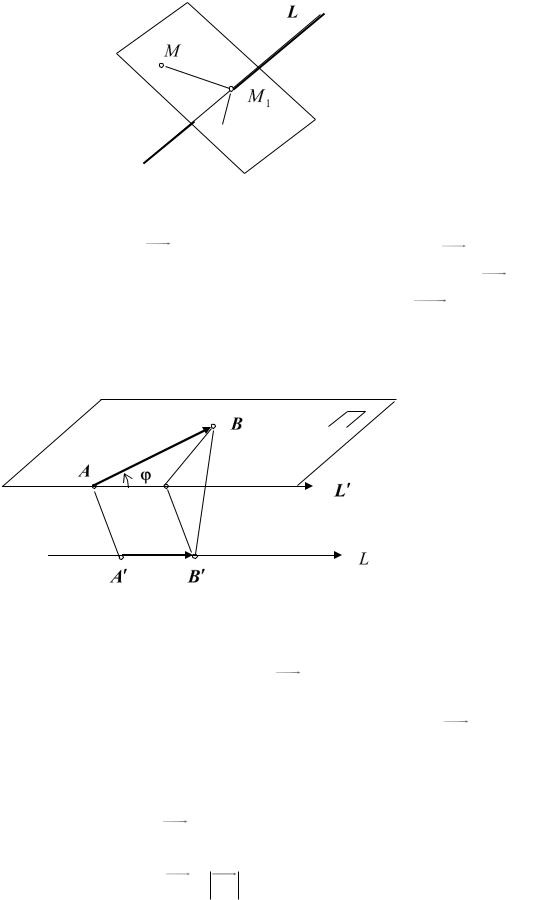
5.3. Проекция вектора на ось. Напомним, что проекцией точки M

на ось L в пространстве называется точка M1 пересечения оси L и плоскости, проходящей через точку M перпендикулярно этой оси (рис. 5.8).

38

[Введите текст]

Рис. 5.8

Проекцией вектора AB на ось L называется число ПрL AB , равное по модулю расстоянию между проекциями начала и конца вектора AB на

ось L , и взятого со знаком плюс, если направление вектора A B совпадает с направлением оси, и со знаком минус, если они направлены в противоположные стороны.

понимать меньший из углов, который отсчитывается от направления оси до направления вектора. При этом луч, совмещающий направление оси с

направлением вектора поворачивается на угол 0 1800 .

Теорема. Пусть вектор AB составляет с направлением оси L угол

. Тогда верна формула

ПрL AB AB cos .

39