
10310
.pdf
[Введите текст]
x y 7 z 2 3 5 2
и найти её проекцию на эту прямую.
Выберем точку на прямой M1 (0, 7, 2) , тогда M1M 0 {2,6,1}. Вычис-
лим скалярное произведение M1M 0 , S 38 , |
квадрат модуля |
| S |2 38 |
|||||
направляющего вектора |
S { 3 , 5 , ,2 }и по формуле (12.9) |
|
получим |
||||
M1M 2 {3,5, 2}: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
d | 2i 6 j k (3i 5 j 2k ) | | i j k | 3 . |
|
|
|||||
Координаты проекции |
точки |
M 2 (x2 , y2 , z2 ) |
находим из |
равенства |
|||
M1M 2 {x2 0, y2 7, z2 2} M 2 (3, 2, 4) , поэтому окончательно получаем
M 2 (3, 2, 4) .
В частности, таким способом можно находить расстояние между параллельными прямыми в пространстве как расстояние от точки, взятой на одной прямой, до другой прямой.
12.3. Пересечение прямых в пространстве. Пусть две прямые L1 и L2
заданы каноническими уравнениями
L : |
x x1 |
|
y y1 |
|
z z1 |
, |
L : |
x x2 |
|
y y2 |
|
z z2 |
. |
|
|
|
|
|
|
||||||||
1 |
m1 |
|
n1 |
|
p1 |
2 |
m2 |
|
n2 |
|
p2 |
||
|
|
|
|
|
|
||||||||
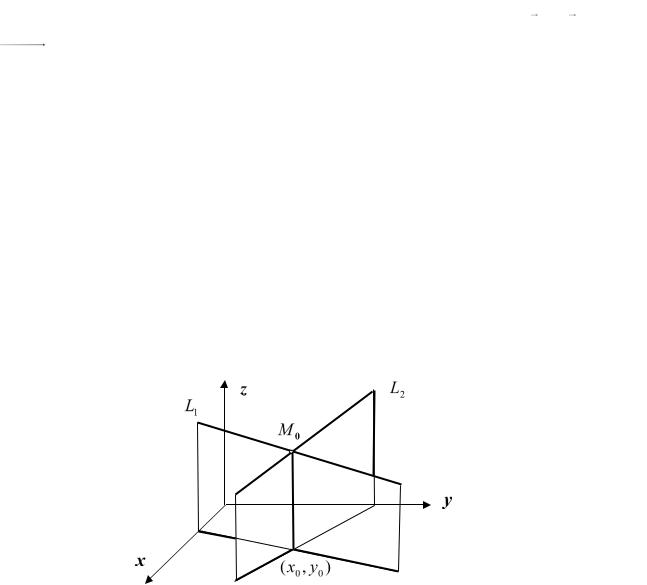
Выясним условия пересечения этих прямых. Предполагаем, что направля-
ющие векторы этих прямых S1 {m1, n1, p1} и S2 {m2 , n2 , p2} не коллинеарны, что исключает случаи параллельности или совпадения этих прямых, и, кроме того, точки M1 (x1, y1, z1 ) и M 2 (x2 , y2 , z2 ) различные (см. рис.12.6).
Рис. 12.6
90
[Введите текст]
Ясно, что прямые будут принадлежать одной плоскости, а значит пере-
секаться в точке |
M 0 , тогда и только тогда, когда три вектора S1 , S2 и |
|||||
M1M2 {x2 x1, y2 |
y1, z2 z1} компланарны. |
В координатной форме это |
||||
условие выглядит так |
|
|
|
|
||
|
|
x2 x1 |
y2 y1 |
z2 z1 |
|
|
|
|
|
||||
|
|
m1 |
n1 |
p1 |
|
0 . |
|
|
m2 |
n2 |
p2 |
|
|
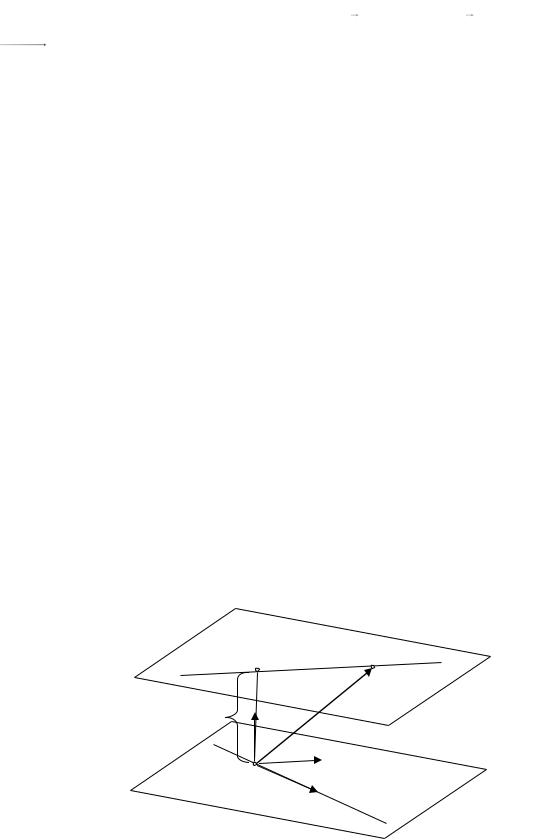
Как найти координаты точки пересечения прямых? Проведём через каждую прямую плоскость, проецирующую эту прямую на какую-нибудь из координатных плоскостей. Например, рассмотрим плоскости, проецирующие эти прямые на плоскость xOy . Пересечение этих плоскостей – это пря-
мая, перпендикулярная плоскости xOy . Координаты точки пересечения этой прямой с плоскостью xOy совпадают с соответствующими координатами точки пересечения данных прямых (см. рис. 12.7).
Рис.12.7
Нахождение координат точки (x0 , y0 ) сводится к решению системы
x x |
|
|
|
y y |
|
|
||||
|
1 |
|
|
|
1 |
|
|
|||
|
m1 |
|
|
n1 |
|
|
||||
|
|
|
|
|
|
, |
||||
|
|
x x |
|
|
|
|
y y |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
n |
2 |
|
||
|
2 |
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
2 |
|
|
||
а третья координата может быть найдена из уравнения прямой L1 или L2 . Пример. Доказать, что прямые
L : |
x 5 |
|
y 4 |
|
z 5 |
, |
L : |
x 5 |
|
y 16 |
|
z 6 |
|
|
|
|
|
|
|||||||
1 |
3 |
|
6 |
2 |
|
2 |
4 |
|
12 |
3 |
||
|
|
|
|
|
||||||||
|
|
|
|
91 |
|
|
|
|
|
|
||
[Введите текст]
пересекаются и найти координаты точки их пересечения M 0 (x0 , y0 , z0 ) Про-
веряем компланарность тройки векторов |
S1 {3, 6, 2}, |
S2 {4, 12,3} и |
||||||||||
M1M 2 {0,12, 1} , вычисляя определитель: |
|
|
|
|
|
|
|
|||||
|
12 |
1 |
|
6 |
2 |
|
3 |
6 |
|
0 . |
||
|
0 |
|
|
|
||||||||
|
|
|
|
|||||||||
|
3 |
6 |
2 |
12 |
|
|
||||||
|
4 |
12 |
3 |
|
12 |
3 |
|
4 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, эти прямые пересекаются. Координаты точки пересечения находим, решая, например, систему
x 5 |
|
|
y 4 |
|
|||||
|
3 |
|
|
|
6 |
|
. |
||
|
|
x 5 |
|
|
|
y 16 |
|||
|
|
|
|
|
|||||
|
4 |
|
|
12 |
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
Её решение x0 7, y0 20 . Из уравнения, допустим, первой прямой найдем третью координату z0 3 . Итак, точка пересечения этих прямых
M 0 (7, 20,3).
12.4. Расстояние между двумя прямыми. Случай параллельных пря-
мых мы рассматривали в п.12.2. Поэтому пусть прямые скрещивающиеся, следовательно, расположены в параллельных плоскостях (см. рис. 12.8), расстояние между которыми и будет искомым расстоянием между прямыми.
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
1 |
1 |
|
1 |
Рис.12.8
92

[Введите текст]
Пусть прямые заданы каноническими уравнениями
L : |
x x1 |
|
y y1 |
|
z z1 |
, |
L : |
x x2 |
|
y y2 |
|
z z2 |
|
|
|
|
|
|
|||||||
1 |
m1 |
|
n1 |
|
p1 |
2 |
m2 |
|
n2 |
|
p2 |
|
|
|
|
|
|
|
|||||||
Кратчайшее расстояние между прямыми найдём как абсолютную величину
проекции вектора |
1 2 |
на вектор |
= 1 |
× 2 . |
|
|
|
|||||||||||
Пример. Найти расстояние между прямыми |
|
|
|
|||||||||||||||
|
+ 1 |
|
|
|
− 1 |
|
|
+ 1 |
|
− 2 |
|
|||||||
1 : |
|
|
|
= |
|
= |
|
|
|
; |
2 : |
|
= |
|
|
= |
|
; |
|
1 |
|
1 |
2 |
|
1 |
3 |
|
4 |
|||||||||
Вектор 1 2 = {1, −1, 1}. |
Находим векторное произведение |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= 1 × 2 = |1 1 |
2| = −2 − 2 + 2 . |
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
3 |
4 |
|
|
|
|
|
|
|
||
Удобнее находить проекцию на вектор = {1, 1, −1} , коллинеарный вектору . Тогда
= Пр |
|
= |
∙ 1 2 |
= |
|1 − 1 |
+ 1| |
≈ 0.58. |
|
|
|
|
|
|||||
|
1 2 |
|
|
|
√3 |
|||
|
|
|
|
|||||
Лекция 13. Взаимное расположение прямых и плоскостей
13.1. Угол между прямыми в пространстве. Пусть заданы две прямые
L1 и L2 своими каноническими уравнениями
Если m1 n1 m2 n2
S1 {m1, n1, p1}
L : |
|
x x1 |
|
|
y y1 |
|
|
z z1 |
|
|
|||
|
|
|
|
|
|
||||||||
1 |
|
m1 |
|
|
n1 |
|
|
|
p1 |
||||
|
|
|
|
|
|
|
|||||||
L : |
x x2 |
|
y y2 |
|
|
z z2 |
. |
||||||
|
|
|
|
||||||||||
2 |
|
m2 |
|
|
n2 |
|
|
|
p2 |
||||
|
|
|
|
|
|
|
|||||||
p1 , что означает коллинеарность направляющих векторов p2
и S2 {m2 , n2 , p2}, то прямые L1 и L2 параллельны и угол
93
[Введите текст]
между ними полагают равным нулю. Параллельные прямые, очевидно, принадлежат одной плоскости.
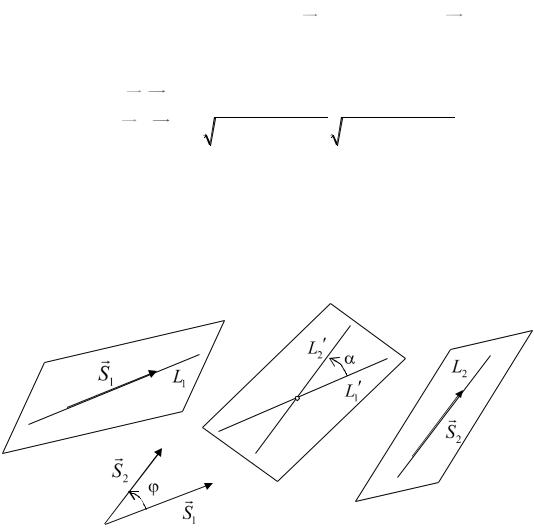
Под углом между пересекающимися прямыми будем понимать уголмежду их направляющими векторами S1 {m1, n1, p1} и S2 {m2 , n2 , p2}, если он острый, и угол в противном случае. Следовательно,
cos | cos | |
| S1, S2 | |
|
|
| m1 m2 n1 n2 p1 p2 |
| |
|
. |
|
(13.1) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
S |
|
|
S |
2 |
|
m 2 |
n 2 |
p 2 m |
2 n 2 |
p 2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
|
|
|
1 |
1 |
1 |
2 |
2 |
2 |
|
|
|
|
|||
Прямые, не лежащие в одной плоскости, называются скрещивающи- |
|||||||||||||||||||||
мися прямыми. Определим понятие угла |
между скрещивающимися пря- |
||||||||||||||||||||
мыми. Под углом |
|
между двумя прямыми |
L1 и L2 будем понимать |
||||||||||||||||||
наименьший из углов |
|
между пересекающимися |
прямыми L |
и |
L , им |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
параллельными (см. рис.13.1).
Рис. 13.1
В частности, условие перпендикулярности двух прямых имеет вид
|
|
|
L1 L2 |
m1m2 n1n2 p1 p2 0 . |
|||||
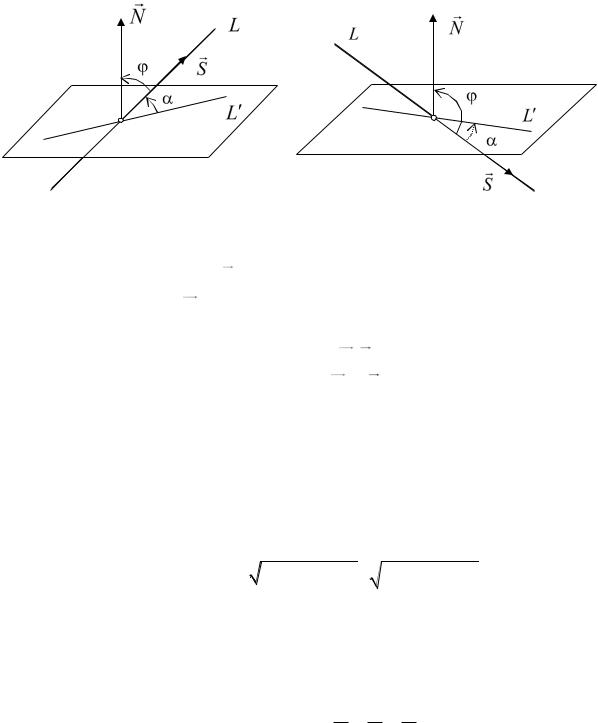
13.2. Угол между прямой и плоскостью. Найдем теперь угол между |
|||||||||
прямой |
|
|
|
|
|
|
|
|
|
|
L : |
x x0 |
|
y y0 |
|
z z0 |
|
(13.2) |
|
|
|
|
|
||||||
|
|
|
m |
n |
p |
|
|||
и плоскостью П : Ax By Cz D 0 . |
Напомним, |
что под углом между |
|||||||
прямой и плоскостью понимают наименьший положительный угол |
|||||||||
между проекцией |
|
прямой |
L на плоскость П |
и прямой L (см. рис. |
|||||
L |
|||||||||
13.2). |
|
|
|
|
|
|
|
|
|
94
[Введите текст]
|
|
|
|
|
Рис. 13.2 |
|
|
|
|
|
|
|
|||
|
Вычисление угла |
можно свести к вычислению угла |
|
между |
|||||||||||
направляющим вектором |
S {m, n, p} прямой |
L |
и нормальным к плос- |
||||||||||||
кости |
П вектором |
N {A, B,C}. В случае острого угла |
0 / 2 |
||||||||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin cos N, S . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
| N | | S | |
|
|
|
|
|
|
|||
В случае тупого угла |
/ 2 , |
так как |
|
(см. рис. 13.2), |
полу- |
||||||||||
2 |
|||||||||||||||
чим |
sin sin( |
) cos . |
Таким образом, |
для вычисления угла |
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
между прямой и плоскостью получаем формулу |
|
|
|
|
|
|
|
||||||||
|
sin | cos | |
|
|
| mA nB pC | |
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
A2 |
B2 C2 |
m2 n2 p2 |
|
|
||||||
В частности, условие перпендикулярности и условие параллельности прямой и плоскости имеют вид
L П mA Bn Cp ;
L || П Am Bn Cp 0 .
В последнем случае, если дополнительно выполняется равенство
Ax0 By0 Cz0 D 0 ,
95

[Введите текст]
которое означает, что точка (x0 , y0 , z0 ) прямой L принадлежит плоскости П
, то прямая лежит в этой плоскости. Таким образом, принадлежность прямой, заданной каноническими уравнениями (13.2), плоскости П : Ax By Cz D 0 определяется выполнением условий
Am Bn Cp 0
Ax0 By0 Cz0 D 0 .
Если прямая L задана как линия пересечения двух плоскостей
A1x B1 y C1z D1 0
A2 x B2 y C2 z D2 0 ,
то ее направляющий вектор может быть получен как векторное произведение нормальных векторов этих плоскостей (см. рис. 12.3), т.е.
SN1 N2 ,
изадача нахождения угла между прямой и плоскостью сводится к преды-
дущей. В этом случае
N1 N2 , N |
|
(N1, N2 , N ) |
|
||||||
sin | N1 N2 | | N | |
|
|
|
|
. |
|
|||
| N1 N2 | | N | |
|
||||||||
13.3. Пересечение прямой с плоскостью. Вычислим теперь коорди- |
|||||||||
наты точки пересечения прямой L : |
x x0 |
|
y y0 |
|
z z0 |
и плоскости |
|||
|
n |
|
|||||||
|
|
m |
|
|
|
p |
|
||
П : Ax By Cz D 0 при условии, что они пересекаются. Перейдём от канонических уравнений прямой к параметрическим
x x |
|
y y |
|
z z |
|
|
|
x mt x0 |
|
|
|
0 |
|
|
|
|
|||
0 |
|
0 |
|
|
t |
|
y nt y0 |
||
m |
n |
p |
|
||||||
|
|
|
|
|
z pt z |
|
|||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Найдем значение параметра t1 , при котором соответствующая точка прямой принадлежит плоскости, т.е. удовлетворяет уравнению
A mt x0 B nt y0 C pt z0 D 0
или, что тоже,
( Am Bn Cp)t ( Ax0 By0 Cz0 D) . |
(13.2) |
96 |
|
[Введите текст]
Если Am Bn Cp 0 и Ax0 By0 Cz0 D 0 , то это уравнение не имеет
решений. Эти условия соответствуют тому, как мы выяснили выше, что прямая и плоскость параллельны и, следовательно, не пересекаются. Если Am Bn Cp 0 и Ax0 By0 Cz0 D 0 , то уравнение (13.2) имеет бес-
численное множество решений, т.е. прямая принадлежит плоскости. И, наконец, если Am Bn Cp 0 , то
t1 |
|
Ax0 By0 |
Cz0 |
D |
. |
|
Am Bn Cp |
||||||
|
|
|
||||
Подставим это значение в параметрические уравнения прямой и найдем x1, y1, z1 – координаты точки пересечения прямой L с плоскостью П .
Если прямая L задана как линия пересечения двух плоскостей
A1x B1 y C1z D1 0
A2 x B2 y C2 z D2 0 ,
а плоскость задана уравнением Ax By Cz D 0 , то координаты точки
их пересечения находим, решая следующую систему трех линейных уравнений:
Ax By Cz D 0 |
||||
|
A1x B1 y C1z D1 0 . |
|||
|
||||
A x B y C z D 0 |
||||
|
2 |
2 |
2 |
2 |
Здесь возможны варианты. Если определитель матрицы этой системы не равен нулю, то искомая точка пересечения единственна и находится, например, по правилу Крамера. Если определитель матрицы этой системы равен нулю, что означает компланарность нормальных векторов к этим плоскостям, то система может быть несовместна (см., например, рис. 13.3)
Рис. 13.3
97
[Введите текст]
или иметь бесчисленное множество решений, когда эти три плоскости пересекаются по одной прямой (см. рис. 13.4).
Рис. 13.4
Лекция 14. Другие задачи о прямых и плоскостях
Рассмотрим несколько типичных задач получения уравнений прямых или плоскостей, обладающих заданными свойствами.
Задача 1. Составить уравнения прямой L , проходящей через данную точку M x0 , y0 , z0 перпендикулярно к данной плоскости П : Ax By Cz D 0
.
98

[Введите текст]
= { , , }
0 0, 0, 0
L 
Рис. 14.1
Очевидно, что в качестве направляющего вектора прямой можно взять нормальный вектор к плоскости, т.е. S N {A, B,C}. Отсюда следует, что уравнения искомой прямой имеют вид
x x0 |
|
y y0 |
|
z z0 |
. |
(14.1) |
|
|
|
||||
A |
|
B |
|
C |
|
|
Задача 2. Составить уравнение плоскости П , проходящей через данную точку M1 (x1, y1, z1 ) перпендикулярно к данной прямой L
x x0 |
|
y y0 |
|
z z0 |
. |
|
|
|
|||
m |
|
n |
|
p |
|
Очевидно (см. рис. 14.2), что в качестве нормального вектора плоскости можно взять направляющий вектор прямой, т.е. N s m, n, p . Отсюда следует, что уравнения искомой плоскости имеет вид
m x x1 n y y1 p z z1 0. |
(14.2) |
Рис. 14.2
99
