9818

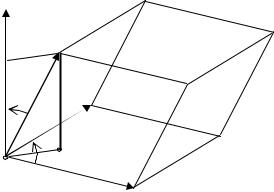
[Введите текст]

Теперь, что касается модуля смешанного произведения. Рассмотрим рисунок

где V – объем параллелепипеда, построенного на векторах a , b , c . Итак, смешанное произведение некомпланарных векторов по модулю

равно объему параллелепипеда, построенного на этих векторах.

Нам осталось только научиться вычислять смешанное произведение векторов, заданных своими координатами. Пусть

[Введите текст]

Итак, мы получили выражение смешанного произведения через координаты сомножителей

Часто возникает задача вычисления объема пирамиды по координатам ее вершин. Сведем эту задачу к вычислению объема параллелепипеда. Для этого разделим параллелепипед диагональным сечением на две равновеликих призмы

c

b

a

Рис. 8.10

В свою очередь каждую из полученных призм можно разделить на три равновеликих пирамиды.

Рис. 8.11

61

[Введите текст]

Таким образом, объем пирамиды равен 1/ 6 от объема параллелепипеда, построенного на этих же векторах, т.е.

В заключение этой темы обратимся к геометрической интерпретации однородных систем линейных уравнений. Однородная система линейных уравнений всегда совместна, поскольку ранг расширенной матрицы совпадает с рангом основной матрицы. Одно из её решений очевидно. Это нулевое решение. Его называют тривиальным. Естественно возникает вопрос о существовании других решений. В «солидных» курсах алгебры доказывается, что для существования нетривиальных решений необходимо и достаточно, чтобы определитель системы однородных уравнений был равен нулю. Это утверждение становится очевидным (в трёхмерном случае), если сформулировать задачу на «языке» векторной алгебры.

Действительно, так как линейное уравнение вида a1x1 + a2 x2 + a3 x3 = 0

Очевидно, что такой ненулевой вектор x существует тогда и только тогда,

и есть условие компланарности этих векторов.

62

[Введите текст]

Раздел 3. Аналитическая геометрия. Прямые и плоскости

Лекция 9. Прямая линия на плоскости

Любая точка на плоскости однозначно определяется упорядоченной парой чисел – ее декартовыми координатами. Также и вектор на плоскости задается парой своих декартовых координат. В этой и ближайших лекциях мы получим аналитические представления для таких геометрических объектов, как прямая на плоскости, плоскость и прямая в пространстве.

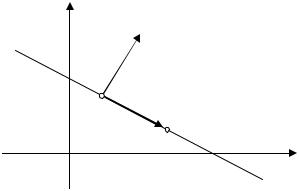
9.1. Общее уравнение прямой. Пусть на плоскости с декартовой прямоугольной системой координат проведена прямая L , и мы хотим получить уравнение, связывающее координаты любой точки, принадлежащей этой прямой.

y

Раскрывая в (9.1) скобки, получим уравнение

[Введите текст]

где для краткости обозначено C = − Ax0 − By0 .

Уравнение (9.2) называют общим уравнением прямой на плоскости. Обратим внимание, что уравнение прямой на плоскости является линейным уравнением относительно переменных x и y , а коэффициенты при

них – соответствующие координаты нормального к этой прямой вектора

N = { A, B } .

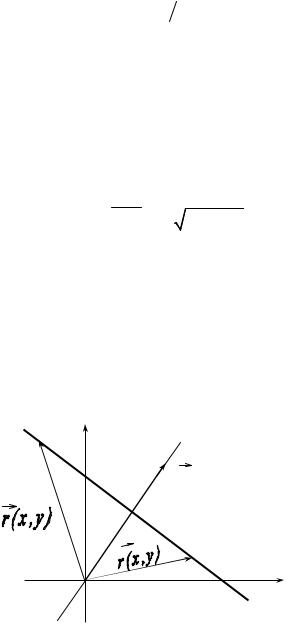
Обратно, покажем, что уравнение вида (9.2) определяет прямую на плоскости и построим эту прямую. По данным числам A и B образуем

уравнению (9.2), имеют одну и ту же проекцию на фиксированный вектор

Отсюда следует алгоритм построения прямой по заданному уравнению (9.2). Через начало координат проведем прямую в направлении вектора

воположном направлении, если p < 0 . Через конец P этого отрезка проводим перпендикулярно ему требуемую прямую L .

y

N

P

p

M( x, y) x

O

L

Рис. 9.2

64

[Введите текст]

Построение прямой производится гораздо проще, если воспользо-

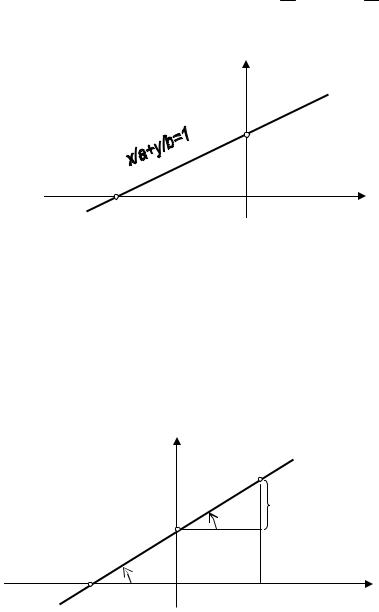
ваться так называемым уравнением прямой в отрезках

нат, соответственно.

Действительно, из (9.2) следует Ax + By = −С и далее, предполагая, что A ¹ 0, B ¹ 0,C ¹ 0 (т.е. прямая не проходит через начало координат и не параллельна координатным осям) и разделив обе части этого уравнения на

−C , получим уравнение (9.3), в котором a = − C и b = − C величины от-

Рис. 9.3

9.2. Уравнение прямой с угловым коэффициентом. Иногда уравне-

ние прямой удобно представить в другом виде. Пусть прямая L пересекает ось ординат в точке (0,b) и образует с положительным направлением оси абсцисс угол α , тангенс которого обозначим через k = tgα .

O

Рис. 9.4

65

Пусть точка M 0 ( x0 , y0 ) L , тогда y0 = kx0 + b . Выражая отсюда b и

подставляя в (9.4), получим уравнение прямой с угловым коэффициентом k , проходящей через заданную точку, в виде

Заметим, что меняя в уравнении (9.5) величину k , мы получим множество прямых, проходящих через данную точку. Это множество прямых называется пучком прямых, проходящих через заданную точку.

9.3. Параметрические и каноническое уравнения прямой. Уравне-

ние прямой L можно получить, задавая точку M 0 ( x0 , y0 ) и её направ-

ляющий вектор S = {m,n} (см. рис. 9.5).

S M

L

M 0

Рис. 9.5

Пусть M (x, y) L – произвольная точка. В силу коллинеарности векторов

66

[Введите текст]

Это так называемые параметрические уравнения прямой. Ясно, что при изменении значения параметра t в пределах от −∞ до +∞ точка M (x, y)

mn

Вчастности, если одна из координат направляющего вектора равна

нулю, например, S = {m,0}, то получаем уравнение прямой y = y0 .

В качестве следствия из уравнения (9.7) получим уравнение прямой, проходящей через две заданные точки M1 ( x1, y1 ) и M 2 ( x2 , y2 ) . Как известно, прямая определяется двумя своими точками. Нетрудно понять, что вектор

M1M 2 = { x2 − x1; y2 − y1}

можно считать направляющим вектором данной прямой. Отсюда получим

уравнение прямой, проходящей через две заданные точки

67

[Введите текст]

Лекция 10. Прямые линии на плоскости

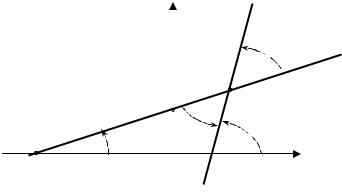
10.1. Взаимное расположение двух прямых. Пусть сначала две прямые заданы уравнениями с угловым коэффициентом:

угольника равен сумме внутренних углов, с ним не смежных). Отсюда следует, что ϕ = α2 − α1 ,

[Введите текст]

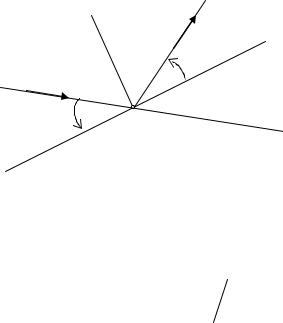
Иногда по заданному углу между прямыми и известному угловому коэффициенту одной из прямых нужно найти угловой коэффициент другой прямой. Поэтому нужно быть внимательными при применении формулы (10.1). Чтобы подчеркнуть, какой угол вычисляется по этой формуле, в ней ставят стрелку, показывающую, что угол отсчитывается от прямой с угло-

Получить уравнение прямой, по которой направлен отражённый луч.

Рис. 10.2

Из аналогичной формулы для тангенса угла «отражения» α

x - 2 y + 5 = 0

Из уравнения пучка прямых y − y0 = k ( x − x0 ) получаем уравнение искомой прямой 29x − 2 y + 33 = 0 .

69