
9818
.pdf
[Введите текст] |
|
Допустим обратное, т.е. a > b |
(см. рис. 16.3). Рассмотрим непересе- |
кающиеся ε -окрестности точек a и |
b , ε < (a − b) / 2 . Тогда, начиная с не- |
которого номера N , члены последовательности xn будут находиться в
ε-окрестности точки a , а члены последовательности yn будут находиться
вε -окрестности точки b , т.е.
|
|
x |
n |
− a |
|
|
< ε |
|
|
|
|
|
|
||||||
n > N : |
|
|
|
|
|
|
|
xn > yn , |
|
|
y |
|
− b |
|
|
< ε |
|
||
|
|
|
|
||||||
|
|
n |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
что противоречит предположению xn ≤ yn .
|
yn |
|
|
x n |
|
b − ε |
b |
b + ε |
a − ε |
a |
a + ε |
Рис. 16.3
Заметим, что из строгого неравенства для членов последовательности следует, вообще говоря, нестрогое неравенство для их пределов: например,
|
x |
= |
1 |
< |
y |
|
= |
3 |
, |
ноlim x |
= lim y |
|
|
|
|
|
||||
|
|
n |
|
n |
|
|
|
|
||||||||||||
|
n |
|
n |
|
|
n |
|
n→∞ |
n |
|
n→∞ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следствие для трех последовательностей: |
|
|
|
|
|
|
|
|||||||||||||
lim x |
= a, |
lim y |
= a, |
x |
≤ z |
|
≤ y |
lim z |
|
= a. |
|
|
||||||||
n→∞ n |
|
n→∞ n |
|
|
|
|
n |
|
n |
|
n |
|
n→∞ |
n |
|
|
|
|||
Пример. Рассмотрим последовательность |
x = αn |
, где α |
n |
n -я цифра |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
числа π в его десятичном представлении. Предел этой последовательности
равен нулю так как
0 ≤ αn ≤ 9 , n n n
т.е. она заключена между двумя последовательностями, имеющими общий предел равный нулю.
3. Предел суммы (разности) двух сходящихся к конечным пределам последовательностей равен сумме (разности) их пределов
lim(x ± y ) = a ± b.
n→∞ n n
110
[Введите текст]
Действительно, поскольку |
lim xn = a , то для заданного |
|
|
ε 2 найдётся |
||||||||||||||||||
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
< ε 2 . |
||||
такой номер N1 последовательности xn , что n > N1 |
|
|
xn − a |
|
||||||||||||||||||
|
|
|||||||||||||||||||||
Аналогично для последовательности |
yn N2 : n > N2 |
|
yn − b |
|
< ε 2 . |
|||||||||||||||||
|
|
|||||||||||||||||||||
Тогда n > N = max{N1, N2} выполняется неравенство |
|
|
|
|
|
|
ε |
|
|
|
ε |
|
|
|
||||||||
| (x |
+ y |
) − (a + b) |=| (x |
|
− a) + ( y |
|
− b) |≤| x − a | + |
| y |
|
− b |< |
+ |
= e , |
|||||||||||
n |
n |
n |
|
|
||||||||||||||||||
n |
n |
|
|
|
n |
|
|
|
|
2 |
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
что и доказывает указанное свойство. Здесь мы применили замечательное неравенство
| x + y | ≤ | x | + | y |,
которое для любого числа слагаемых формулируется так: абсолютная ве-
личина суммы не превосходит суммы абсолютных величин слагаемых.
Докажем это неравенство для двух слагаемых. Сложив очевидные неравенства
− | x |≤ x ≤| x |
,
− | y |≤ y ≤ | y |
получим
−(| x | + | y |) ≤ x + y ≤| x | + | y |.
Это двойное неравенство эквивалентно доказываемому неравенству.
4. Предел произведения двух сходящихся к конечным пределам последовательностей равен произведению их пределов
lim xn yn = ab .
n→∞
Это свойство следует из неравенств
| xn yn − ab |=| xn yn + xnb − xnb − ab |=| xn ( yn − b) + b(xn − a) |≤
£| x | ×| y |
|
- b | + | b | ×| x - a |£ M |
ε |
+ | b | |
ε |
= e . |
n |
|
|
||||
n |
n |
2 |
|
2 |
1 |
|
|
|
|
|
|
5. Предел частного двух сходящихся к конечным пределам последовательностей при условии, что предел делителя отличен от нуля, равен частному их пределов
111
[Введите текст]
lim |
xn |
= |
a |
( b ¹ 0 ). |
|
|
b |
||||
n→∞ y |
n |
|
|
||
|
|
|
|
|
|
Доказательство следует из следующей оценки разности
| xn - a | = | xnb - yna | = | xnb - ab + ab - yna | £
yn b |
byn |
|
|
|
byn |
|||
£ |
1 |
(| x |
- a | + | |
a |
| ×| y |
|
- b |). |
|
|
|
n |
||||||
|
| yn | |
n |
|
b |
|
|||
|
|
|
|
|
||||
6. Неубывающая и ограниченная сверху последовательность имеет предел (см. рис.16.4). Невозрастающая и ограниченная снизу по-
следовательность имеет предел.
1
0.8
0.6
0.4
0.2
0
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Рис. 16.4
Это свойство будем считать интуитивно ясным и поэтому ограничимся его геометрической иллюстрацией и простым примером. Например, по-
следовательность x |
= 1 − |
1 |
возрастает и ограничена сверху, значит |
|||
2n |
||||||
n |
|
|
1 |
|
||
|
|
|
lim(1 − |
) = 1. |
||
|
|
|
|
|||
|
|
|
n→∞ |
2n |
||
Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.
Пусть последовательность xn ограничена, т.е. n | xn |< M , а yn → 0. Тогда неравенство
0 ≤| xn yn |≤ M | yn |→ 0 ,
и следствие из свойства 3 всё и доказывают.
112
[Введите текст]
16.2. Второй замечательный предел. Применим понятие предела последовательности для определения одного замечательного числа. Рассмотрим последовательность
|
|
|
|
1 n |
|
xn |
= |
1 |
+ |
|
. |
|
|||||
|
|
|
|
n |
|
Непосредственные вычисления нескольких первых членов последовательности показывают их рост с увеличением номера:
x1 = 2; |
x2 = 2.25; |
x3 = 2.37; x4 = 2.44; x5 = 2.49; x6 = 2.52;K |
|
Можно доказать, |
что xn |
– возрастающая последовательность и ог- |
|
раничена сверху, например, |
xn < 3, n . Согласно свойству 7 она имеет |
||
предел при |
n → ∞ . Предел этой последовательности оказался числом ир- |
||
рациональным, но настолько важным для математики и её приложений, что получил собственное имя
e ≈ 2.718281828459045K
По традиции предел
|
|
|
1 |
n |
|
|
|
|
|
lim 1 |
+ |
|
|
= e |
|
|
|
(16.1) |
|
|
|
|
|
|
|||||
n→∞ |
|
|
n |
|
|
|
|
||
называют вторым замечательным пределом. Из (16.1) следует, что |
|||||||||
|
1 |
|
|
|
|
|
|
|
|
lim (1 + αn ) |
|
= e , |
|
|
|
(16.2) |
|||
αn |
|
|
|
||||||
n→∞ |
|
|
|
|
|
|
|
|
|
где αn – последовательность, стремящаяся к нулю ( αn |
= |
1 |
> 0 ). |
|
|||||
|
|
||||||||
|
|
|
|
|
|
|
n |
|
|
Покажем одну из задач, в которой возникает столь необычный пре- |
|||||||||
дел. Пусть в банк помещён вклад a0 |
|
и по нему выплачивается |
k % в год. |
||||||
Через год величина вклада с учетом начисленных процентов будет следующей:
|
a1 = a0 |
+ a0 |
|
k |
= a0 |
|
+ |
|
|
k |
|
|
, |
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
100 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|||||||
т.е. через один год каждая денежная единица возрастает в 1 + |
k |
|
раз, |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
поэтому через два года вклад примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
a |
|
= a |
|
1 + |
|
|
|
k |
= a |
|
1 |
+ |
|
|
k |
|
2 |
, |
|
|
|
|||
2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
100 |
|
|
|
|
|
100 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
113 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[Введите текст] |
|
|
|
|
|
|
|
а через n лет a |
= a |
|
1 |
+ |
|
k |
n . |
|
|
|
|||||
n |
0 |
|
|
100 |
|
||
|
|
|
|
|
|
||
Это формула сложных процентов, её название сложилось исторически, а в самой формуле нет ничего «сложного». Однако начисление процентов по этой формуле имеет определённые неудобства: начисление процентов по вкладу производится только в конце года. А если вкладчик потребует свой вклад через полгода или через месяц? Нужно чаще начислять проценты. Так, если проценты начислять ежеквартально, то в конце года величина вклада будет равна
a0 |
1 |
+ |
k |
|
1 |
4 . |
|
|
|||||
|
|
100 4 |
|
|||
Было замечено, что в этом случае вклад растёт быстрее. Рассмотрим упрощённый пример. Пусть начальный вклад равен 100 р. при 100% годовых. Если процентные деньги прибавлять один раз в конце года, то вклад превратится в 200 р. Если это делать поквартально, то в конце первого квартала вклад будет равен 100(1+0.25)=125 р., через полгода 125(1.25)=156.25 р., а в конце года ≈ 244.14 p . А если начисление процентов производить ещё чаще? Например, при ежедневном начислении процентов каждая денежная единица будет умножаться на величину
|
|
|
1 |
365 |
|
|
1 |
+ |
|
|
≈ 2.715 . |
|
|||||
|
|
|
365 |
|
|
При непрерывном начислении процентов, т.е. при n → ∞ мы получаем
|
|
|
1 n |
||
lim |
1 |
+ |
|
|
= e . |
|
|||||
n→∞ |
|
|
n |
|
|
Таким образом, даже при таком «фантастическом» проценте (к =100%) в конце года вклад увеличится приблизительно в 2.7 раза.
16.3. Раскрытие неопределённостей. |
Приведенные выше свойст- |
ва пределов последовательностей позволяют |
находить предел, минуя об- |
ращение к его определению. Однако на этом пути возникают трудности, связанные с невозможностью непосредственного применения этих свойств. Поясним на примерах. Пусть требуется найти предел отношения двух последовательностей, сходящихся к бесконечности
lim |
xn |
. |
(16.3) |
|
n→∞ yn
114

[Введите текст]
Мы не можем непосредственно применить свойство о пределе частного двух последовательностей. Предварительно необходимо преобразовать это выражение к виду, допускающему применение указанных свойств. В связи
с этим выражение типа (16.3) называется неопределенностью ∞ |
, а его |
|||||||||
|
|
|
|
|
|
|
|
|
∞ |
|
преобразование к виду, позволяющему найти предел, |
– |
раскрытием не- |
||||||||
определенности. |
|
|
|
|
|
|
||||
|
Заметим, что предел (16.3) может оказаться равным |
0 (например, ко- |
||||||||
гда |
x = n , |
y |
n |
= n2 ), равным конечному числу (например, когда |
x = n , |
|||||
|
n |
|
|
|
|
|
|
|
n |
|
y = 7n ) и равным ∞ (например, когда x |
n |
= n3 , y = 7n ), а также этот пре- |
||||||||
n |
|
|
|
|
|
n |
|
= (−1)n n , y = n ). |
||
дел может вообще не существовать (например, когда x |
n |
|||||||||
|
|
|
|
|
|
|
|
|
n |
|
∞ |
Самым |
|
распространенным приемом |
раскрытия |
|
неопределенности |
||||
|
|
числитель и знаменатель представляют |
собой комбинации |
|||||||
|
, когда |
|
||||||||
∞ |
|
|
|
|
|
|
|
|
|
|
степенных функций, является деление того и другого на такую степень n , чтобы неопределенность исчезла. Например,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
|
|
|
= |
1 |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
n2 + 1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
lim |
|
|
= lim |
|
n2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
n→∞ 3n − 2 |
n→∞ |
|
|
3 − |
2 |
|
|
|
|
3 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Неопределенность |
|
|
0 |
|
обозначает выражение типа (16.3), когда по- |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
следовательности в числителе и знаменателе стремятся к нулю. |
||||||||||||||||||||||||||||||||||||
|
|
Неопределенность |
|
(∞ − ∞)раскрывается, |
например, следующим об- |
|||||||||||||||||||||||||||||||
разом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + |
1 − n |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
lim( |
|
n + 1 − n ) = lim |
= 0 . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
( n + |
1 + |
|
n ) |
|
|||||||||||||||
|
|
|
Неопределенность |
|
(0 ×¥) легко сводится к неопределённостям вида |
|||||||||||||||||||||||||||||||
|
0 |
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
, так как произведение можно представить в виде частного |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
0 |
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn × yn = |
|
xn |
= |
|
|
yn |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn |
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Неопределенность |
|
1∞ |
)связана со вторым замечательным пределом, |
|||||||||||||||||||||||||||||||
|
|
( |
|
|
||||||||||||||||||||||||||||||||
она появляется, когда нужно найти предел выражения xn yn , в котором последовательность xn →1 (но не тождественно равна 1!), а последователь-
115
[Введите текст]
ность yn стремится к ∞. Приведем пример раскрытия такой неопределенности:
|
+ |
1 4n |
|
lim 1 |
|
|
|
|
|||
n→∞ |
|
2n |
|
= lim n→∞
1 + |
1 |
2n 2 |
= e |
2 |
|
|
|
|
|
|
, |
||
|
|
|||||
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
где применён предел (16.1).
Заметим, что неопределенность (1∞ ) может быть сведена к неопреде-
ленности (¥ ×0) путем логарифмирования: сначала находим
|
|
|
a = limln(x |
yn ) = lim( y |
n |
ln x ) , |
|
|
|
|
|
|
n→∞ |
n |
n→∞ |
n |
|
|
|
|
|
|
|
|
|
|
|
||
затем сводим неопределенность (0 ×¥) к неопределенности вида ∞ |
|
или |
|||||||
|
|
|
|
|
|
|
∞ |
|
|
|
0 |
|
, затем, раскрывая их, находим a , и, наконец, получаем |
|
|
||||
|
|
|
|
|
|||||
|
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
lim (xn yn ) = ea .
n→∞
Неопределенности (00 ) и(∞0 )раскрывается также путем предвари-
тельного логарифмирования.
116
[Введите текст]
Лекция 17. Предел функции. Непрерывность
17.1. Предел функции. Понятие предела функции служит для исследования функции в окрестностях точек, в которых непосредственное вычисление значения функции вызывает трудности, а также при больших значениях аргумента (в окрестности бесконечности). Интуитивно, предел функции – это определенное число (или бесконечность), к которому неограниченно приближается последовательность значений функции, когда последовательность значений аргумента стремится к некоторому числу или к бесконечности. Поэтому предел функции определим через уже изученное понятие предела последовательности.
Пределом функции y = f (x) , когда x стремится к x0 , называется число A, если для любой последовательности значений аргумента {xn } , сходящейся к x0 , последовательность соответствующих значений функции yn = f (xn ) стремится к A. Это определение как частный случай включает в себя возможность каждому из чисел x0 и A быть бесконечностью.
Согласно определению для вычисления предела функции требуется найти предел последовательности
lim f ( x ) ,
n→ ∞ n
когда {x |
} – любая последовательность, lim x = x . Например, |
lim |
1 |
= ∞ , |
||||||
|
||||||||||
|
n |
|
|
|
n→∞ |
n |
0 |
x→0 x |
||
|
|
|
|
|
|
|
||||
т.к. lim |
1 |
= ∞ для любой последовательности xn |
такой, что lim xn = 0 . |
|||||||
|
||||||||||
n→∞ x n |
|
|
n→ ∞ |
|
|
|
||||
Функция может быть не определена в точке x0 . Например, |
|
|
|
|||||||
|
|
lim |
x2 − 4 |
= lim(x + 2) = 4 . |
|
|
|
|||
|
|
|
|
|
|
|||||
|
|
x→ 2 x − 2 |
x→ 2 |
|
|
|
|
|
||
Если найдутся две последовательности x (1) |
и x ( 2 ) , обе стремящиеся |
|||||||||
|
|
|
|
|
|
n |
n |
|
|
|
к x , такие, что соответствующие |
им последовательности |
f ( x (1) ) и |
||||||||
0 |
|
|
|
|
|
|
|
|
n |
|
f ( xn ( 2 ) ) сходятся к разным пределам (включая случай, когда один из них не существует), то функция не имеет предела в данной точке. Например,
для функции y = |
x |
|
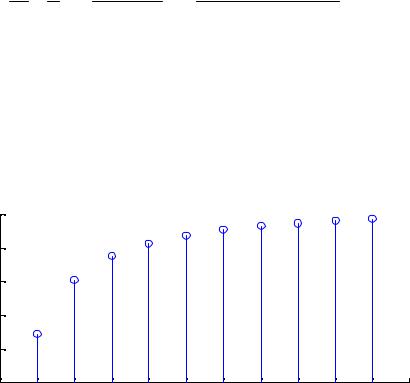
(см. рис. 17.1) не существует предела в точке x =0, |
|||||
|
||||||||
| x | |
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|||
т.к. для стремящихся к нулю последовательностей x (1) = |
1 |
и x ( 2) |
= − |
1 |
по- |
|||
|
|
|
n |
n |
n |
|
n |
|
|
|
|
|
|
|
|
||
лучим
117
[Введите текст]
x1( 2 )
−1
y1( 2 )
lim |
1 |
= 1, lim |
1 |
= −1. |
|
n→∞ x(1) |
n→ ∞ x |
( 2) |
|
|
|
|
1 |
n |
|
|
|
|
|
y |
(1 ) |
y (1 ) |
y (1 ) |
|
|
n |
2 |
1 |
|
|
|
1 |
|
|
|
x1( 2 ) |
|
xn( 2 ) |
|
0,5 |
1 |
|
|
|
|
||
0,5 |
|
x (1 ) |
x (1 ) |
x (1 ) |
|
|
|
n |
|
2 |
1 |
y2( 2 ) |
|
−1 |
|
|
|
|
yn( 2 ) |
|
|
|
|
Рис. 17.1
В последнем примере видно, что для любой положительной последовательности xn > 0 , стремящейся к нулю, соответствующая последовательность значений функции стремится к 1, а для любой отрицательной последовательности xn < 0 , стремящейся к нулю, соответствующая последовательность значений функции сходится к -1. Это наводит на мысль определить так называемые односторонние пределы функции, а именно предел слева и предел справа.
|
Пределом функции y = f (x) слева (справа) |
в точке x0 , называется |
|||||||||||||
число |
A (число B), если для любой последовательности значений аргу- |
||||||||||||||
мента |
xn < x0 |
(xn > x0 ) , |
сходящейся к |
x0 , последовательность соответст- |
|||||||||||
вующих значений функции yn |
= f (xn ) стремится к A (к B). |
Обозна- |
|||||||||||||
чаются эти пределы так: |
|
|
f (x) = A , |
lim f (x) = B . |
|
||||||||||
|
|
|
|
lim |
|
||||||||||
|
|
|
|
x→x0 −0 |
|
|
|
x→ x0 + 0 |
|
|
|
|
|||
В соответствии с этим определением имеем |
|
|
|
|
|||||||||||
|
lim |
x |
= −1, |
lim |
|
x |
= 1, |
lim |
1 |
= −∞ , |
lim |
1 |
= +∞ . |
||
|
|
|
|
|
|
||||||||||
|
x→0−0 | x | |
x→0+0 | x | |
x→0−0 x |
x→0+0 x |
|
||||||||||
Непосредственное вычисление пределов функций осуществляется на основе свойств пределов последовательностей, подробно изложенных в предыдущей лекции. В частности, предел суммы, разности, произведения, частного двух функций равен сумме, разности, произведению, частному их пределов (в случае частного предел знаменателя должен быть отличен от
118
[Введите текст]
нуля). Эти свойства используются для раскрытия неопределенностей при нахождении предела функции аналогично тому, как это делалось при нахождении пределов последовательностей.
17.2. Первый замечательный предел. Продемонстрируем в качест-
ве примера нахождение так называемого первого замечательного преде-
ла
|
lim |
sin x |
= 1. |
(17.1) |
||
|
|
|||||
|
x→0 x |
0 |
|
|||
В данном случае мы имеем неопределенность вида |
. Поскольку |
|||||
0 |
||||||
|
|
|
|
|
||
функция f (x) = sin x |
– чётная и нас интересует её поведение при x → 0, |
|||||
x |
|
|
|
|
|
|
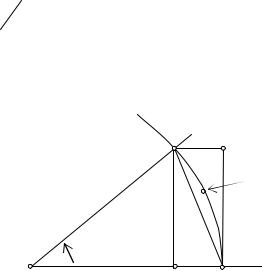
то значение аргумента x , измеряемое в радианах, будем считать положительным и малым. Рассмотрим часть дуги окружности AFC единичного радиуса.
OA = OC = 1 |
A |
B |
AD = sin x |
|
|
DC = 1 − cos x |
|
F |
|
|
|
x
O |
|
|
|
D |
C |
|
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 17.2 |
|
|
||||
Площадь сегмента AFC |
меньше площади прямоугольника ABCD , |
|||||||
поэтому для них имеем неравенство: |
|
|
|
|
|
|||
|
0 < SAFC < SABCD . |
|
(17.2) |
|||||
Площадь сегмента найдём как разность площадей сектора |
OAFC и тре- |
|||||||
угольника OAC |
|
|
|
|
|
|
|
|
SAFC = |
1 |
x − |
1 |
sin x > 0 . |
|
|||
|
|
|
||||||
|
2 |
|
2 |
|
|
|
||
Отсюда следует неравенство |
sin x < x |
|
( x > 0). Полезно представить его |
|||||
графическую иллюстрацию (см. рис. 17.3). Применим это неравенство для оценки площади прямоугольника ABCD
119
