
9818
.pdf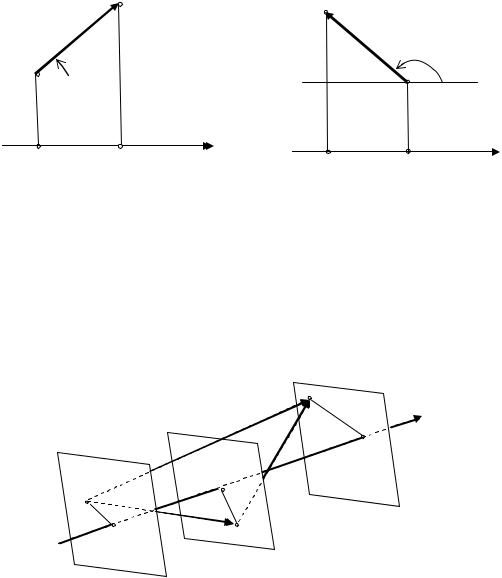
[Введите текст]
Доказательство. В случае, когда угол ϕ острый, утверждение очевидно. В случае тупого угла имеем (см. рис. 5.10)
ПрL AB = − | A1 B1 | = − | AB | cos(π − ϕ) =| AB | cos ϕ
|
|
B |
B |
|
|
A |
ϕ |
|
ϕ |
||
|
|
||||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
L |
|
L |
|
|
|
|
|
|
|
A1 |
B |
B1 |
A1 |
|
|
|
1 |
|
||
|
|
|
Рис. 5.10 |
|
|
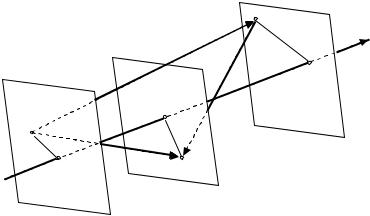
Отметим следующие важные свойства проекции векторов. |
|||||
Свойство 1. |
Проекция суммы векторов на ось равна сумме их проек- |
||||
ций на эту ось (см. рис. 5.11 и 5.12). Точки |
A1 , B1 и |
C1 – проекции точек |
|||
A, B и C на ось |
L . |
|
|
||
|
|
|
|
C |
L |
|
|
|
|
|
C1 |
|
|
A |
|
|
|
A1 B
Рис. 5.11
AC = AB + BC
ПрL AC = A1C1 = A1B1 + B1C1 = ПрL AB + ПрL BC
40
[Введите текст]
C
L
C1
A B1
B
A1
Рис. 5.12
AB = AC + CB
ПрL AB = A1B1 = A1C1 − C1B1 = ПрL AC + ПрL CB .
Свойство 2. Если вектор умножается на число, то его проекция умножается на это же число
ПрL (ka) = k ПрLa .
41
[Введите текст]
Лекция 6. Системы координат
6.1. Линейная комбинация векторов. Выше вектор был определен как геометрический объект – направленный отрезок. Перейдем теперь к эквивалентному его описанию в виде упорядоченного набора чисел. Для этого дадим следующие определения.
Линейной комбинацией векторов |
a1 , a1 , K , am с коэффициентами |
|||
k1 , k2 , K , km называется вектор вида |
|
|
|
|
R |
R |
R |
m |
R |
|
||||
k1a1 |
+ k2a2 + K + km am |
= ∑ ki ai . |
||
i=1
Линейная комбинация называется тривиальной, если все ее коэффициенты равны нулю. Будем говорить, что вектор b выражается в виде линейной комбинации векторов a1, a1, K, am , если он представим в виде
R |
m |
R |
b |
= ∑ki ai . |
|
|
i=1 |
|
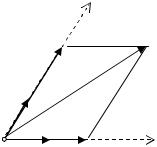
Теорема. Любой вектор a на плоскости единственным образом представим в виде линейной комбинации двух данных неколлинеарных векторов e1 и e2 этой плоскости.
Доказательство. Поместим начала всех трех векторов в некоторую точку O (см. рис. 6.1). Из конца вектора a проведем прямые, параллельные векторам e1 и e2 , и обозначим через P и Q точки их пересечения с осями, «проходящими» через векторы e1 и e2 , соответственно. По прави-
лу сложения векторов имеем R = + . a OP OQ
|
|
|
|
Q |
|
a |
|
|
|
|
e2 |
|
|
|
|
|
O |
e1 |
|
P |
|
|
|
|
|
||
|
|
|
|
Рис. 6.1 |
||
|
R |
R |
, то существуют такие числа a1 и a2 , что |
|||
Так как |
OP || e1 |
и OQ || e2 |
||||
|
|
|
|
R |
, |
R |
|
|
|
OP = a1e1 |
OQ = a2e2 . |
||
|
|
|
|
42 |
|
|
[Введите текст]
Таким образом, получим a = a1e1 + a2e2 .
Покажем теперь, что такое представление единственно. Пусть это не
так, т.е. |
′ |
′ |
Тогда после вычитания получим |
|||
a = a1e1 |
+ a2e2 . |
|||||
|
|
|
′ |
+ (a2 |
′ |
= 0 . |
|
|
|
(a1 − a1 )e1 |
− a2 )e2 |
||
Если хотя бы один из коэффициентов при векторах e1 и e2 , не равен нулю, то отсюда будет следовать их коллинеарность, что противоречит предположению. Таким образом, указанное представление единственно.
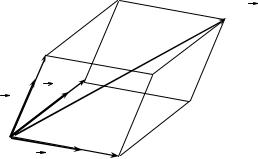
Теорема. Любой вектор a в пространстве единственным образом представим в виде линейной комбинации трех данных некомпланарных векторов e1 , e2 и e3 .
Доказательство этой теоремы проводится аналогично доказательству предыдущей теоремы (см. рис.6.2)
|
a |
R |
|
e2 |
Q |
|
|
e3 |
|
O |
|
e1 |
P |
|
|
|
Рис. 6.2 |
Введем свойство линейной зависимости векторов, обобщающее свойства коллинеарности и компланарности на случай произвольного числа векторов. Векторы a1, a1, K, am называются линейно зависимыми, если хотя бы один из них выражается в виде линейной комбинации остальных, то есть
R |
= |
m |
R |
|
|
(6.1) |
|||
a j |
∑ ki ai |
|||
i=1(i¹ j )
В противном случае эти векторы называются линейно независимыми. Из этих определений следует, что любые два коллинеарных вектора
линейно зависимы, так как из условия a1 || a2 следует, что a2 = ka1 , и что любые три вектора на плоскости также линейно зависимы. Таким образом, приведенные выше теоремы можно переформулировать следующим образом: любой вектор на плоскости единственным образом представим в виде линейной комбинации двух заданных линейно независимых векторов, а любой вектор в пространстве – в виде линейной комбинации трех заданных линейно независимых векторов.
43

[Введите текст]
Возможность такого представления любого вектора приводит к мысли определять вектор и его положение набором коэффициентов его линейной комбинации. Естественно возникают задачи определения положения вектора и его длины через этот набор коэффициентов. Эти задачи решаются с помощью операции скалярного умножения векторов.
6.2. Разложение вектора по базису. Координаты вектора. Базисом
{e1, e2 , e3} называются взятые в определенном порядке линейно независимые векторы. Термин базис (гр. basis – основание) отражает тот факт, что через эти векторы можно выразить любой вектор. Если базисные векторы взаимно перпендикулярны, то базис называется ортогональным, а если плюс к этому базисные векторы имеют единичную длину, то – ортонор-
мированным.
Выражение данного вектора a в виде линейной комбинации базис-
ных векторов называется его разложением в данном базисе (или по бази-
су):
a = a1e1 + a2e2 + a3e3 .
Коэффициенты разложения {a1, a2 , a3} называются координатами векто-
ра a |
в данном базисе, и записывается это так: |
|
|
|
a = { a1, a2 , a3} . |
Таким образом, теперь вектор – это упорядоченная тройка чисел (на |
||
плоскости – |
пара чисел). |
|
Операции над векторами в координатной форме |
||
· |
R |
= b тогда и только тогда, когда ai = bi , i ; |
a |
||
· |
R |
+ b = { a1 + b1, a2 + b2 , a3 + b3} ; |
a |
||
·l × a = { l a1, l a2 , l a3 ,}
непосредственно следуют из определения. Например,
R |
R |
R |
R |
R |
R |
R |
a |
+ b = (a1e1 |
+ a2e2 |
+ a3e3 ) + (b1e1 |
+ b2e2 |
+ b3e3 ) = |
|
= (a1 + b1 )e1 + (a2 + b2 )e2 + (a3 + b3 )e3 ) = {a1 + b1 , a2 + b2 , a3 + b3}.
Условие коллинеарности двух векторов «в координатах» получается
следующим образом: |
R |
|| b |
тогда и только тогда, когда |
R |
или |
a |
b = l × a |
bi = l × ai i , т.е. их соответствующие координаты пропорциональны:
b1 = b2 = b3 . a1 a1 a3
44
[Введите текст]
6.3. Декартова система координат. Декартовой системой коорди-
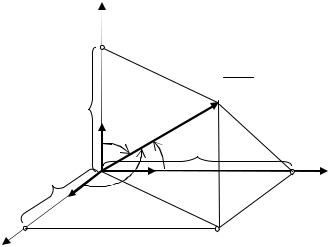
нат называется совокупность фиксированной точки O (начала координат) и базиса векторов {e1, e2 , e3}, исходящих из точки O . Оси, проходящие через базисные векторы, называют соответственно осью абсцисс (ось Ox ), осью ординат (ось Oy ) и осью аппликат (ось Oz ). Плоскости, проходящие через две какие-либо оси, называют координатными плоскостями.
Если базис ортогональный, то такая система координат называется декартовой прямоугольной системой координат. В ортонормированном
базисе единичные базисные векторы принято обозначать через |
i , j , k . |
|
Очевидно, что «в координатах» эти векторы |
записываются следующим |
|
образом: |
|
|
i = {1, 0, 0}, j = {0, 1, 0}, |
k = {0, 0, 1} . |
|
Радиус-вектором произвольной точки |
M называют вектор |
OM , а |
его координаты называют координатами этой точки. Если даны координаты точек A(x1, y1, z1) и B(x2 , y2 , z2 ) , то в силу того, что AB = OB − OA , координаты вектора AB равны
AB = {x2 - x1, y2 - y1, z2 - z1} .
Для произвольной точки M в декартовой системе координат с ортонормированным базисом в разложении вектора
OM = x × i + y × j + z × k
его координаты x, y, z являются проекциями вектора OM на оси Ox, Oy, Oz , соответственно (см. рис. 6.3)
OM = x i + y j + z k
z k
|
|
γ |
y |
|
|
β |
|
x |
α |
j |
|
|
|
||
|
|
|
|
P |
i |
|
|
|
|
|
Q
Рис. 6.3
45
[Введите текст]
Обозначим через α, β, γ углы между положительными направле-
ниями осей координат и вектором OM . Тогда проекции вектора OM выражаются следующим образом:
x = PrOX OM =| OM | cos α , y = PrOY OM =| OM | cosβ , z = PrOZ OM =| OM | cos γ .
В частности, если вектор = R единичной длины, то его координаты
OM e
являются косинусами углов, которые этот вектор образует с осями координат, то есть
e= {cosα, cosβ, cos γ}.
Всвязи с этим координаты единичного вектора называют направляющи-
ми косинусами этого вектора.
Длина вектора может быть найдена по теореме Пифагора: из двух прямоугольных треугольников OMQ и OPQ следует, что
UUUUR
| OM |= x2 + y 2 + z 2 .
Таким образом, углы, которые вектор образует с осями координат, связаны следующим соотношением
R |
2 |
= co s2 α + cos2 β + cos2 γ = 1. |
e |
6.4.Полярная система координат. Кроме декартовой, возможны
идругие системы координат. Рассмотрим полярную систему координат.
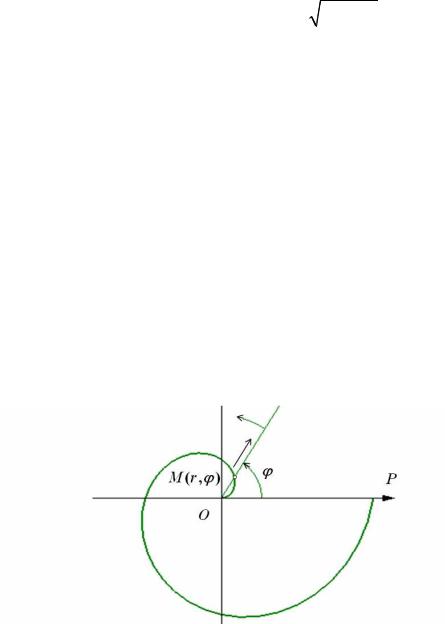
Пусть на плоскости зафиксирована точка O (полюс) и выбран луч (полярная ось OP ) с началом в полюсе (см. рис.6.4)
, φ
r |
r |
Рис. 6.4
46
[Введите текст]
Тогда положение произвольной точки M на плоскости можно однозначно охарактеризовать двумя числами (r,ϕ) , где r =| OM | – расстояние этой
точки от полюса и ϕ – угол между полярной осью и вектором OM , отсчитываемый от полярной оси против часовой стрелки (см. рис. 6.4).
Выберем на плоскости две системы координат – декартову прямоугольную и полярную – так, что полюс находится в начале декартовой системы координат, а полярная ось направлена вдоль положительного направления оси абсцисс. Тогда любая точка M будет иметь декартовы координаты (x, y) и полярные (r,ϕ) . Из рис. 6.4 непосредственно следуют соотношения между полярными и декартовыми координатами (предполагается, что линейный масштаб одинаковый в обеих системах координат)
x = r cos ϕ |
|
|
|
|
|
|
|
|
|
|
x |
2 |
+ y |
2 |
|
||||
r = |
|
|
|
||||||
y = r sin ϕ , |
|
tg ϕ = |
|
y . |
|||||
|
|
|
|
|
|
|
|||
|
|
x |
|
|
|||||
|
|
|
|
|
|
|
|
||
В полярной системе координат удобнее изображать кривую, расстояние точки которой от начала координат (полюса) определяется как функция направления (полярного угла). Например, так называемая «спираль Архимеда» определяется следующим образом: расстояние её точки до полюса пропорционально величине угла между полярной осью и радиу- сом-вектором этой точки. В соответствии с этим запишем уравнение этой кривой в полярной системе координат
r = a × j , a > 0
и построим ее график Спираль Архимеда можно рассматривать как траекторию движения точки, равномерно перемещающейся вдоль прямой, в то время как эта прямая равномерно вращается против часовой стрелки относительно полюса. На рис. 6.5 приведена часть этой спирали, соответствующая изменению полярного угла в пределах одного оборота.
Рис. 6.5
47

[Введите текст]
Лекция 7. Скалярное произведение
7.1. Скалярное произведение двух векторов. Скалярным произве-
дением векторов a и b называется число, равное произведению модулей
этих векторов на косинус угла между ними < R > = R × ϕ a,b | a | | b | cos
b
ϕ
a
Рис. 7.1
Под углом между двумя векторами будем понимать наименьший из двух углов между ними.
Скалярное произведение обозначается символом |
R |
× b |
R |
a |
или < a,b > . |
Обратим внимание на то, что результат этой операции может быть выражен через проекцию одного из векторов на другой. Действительно, так как
|
ПрaRb = | b |cos ϕ , |
ПрbR a =| a|cos ϕ , |
R |
R |
R |
то (см. рис. 7.2) < a,b > =| a | ×ПрaR b =| b | ×ПрbR a |
||
|
R |
R |
|
b |
|
|
ПрRa |
|
|
b |
|
|
ϕ |
|
|
ПраRb |
a |
Рис. 7.2
С этой операцией в физике связано вычисление работы силы F при перемещении материальной точки по направлению вектора S , когда угол между этими векторами равен ϕ . Тогда работа вычисляется по формуле
48
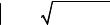
[Введите текст]
A =| F |×| S |cos ϕ = < F, S > .
Операция скалярного произведения позволяет выразить проекцию вектора на вектор и угол между векторами следующим образом:
|
|
R |
> |
|
R |
,b > |
|
R < a,b |
, cos ϕ = |
< a |
|||||
R |
= |
R |
|
R |
R |
, |
|
Пр b a |
| b | |
|
|
||||
|
|
|
|
| a |×| b |
| |
||
причем, если скалярное произведение векторов положительно, то угол между ними острый, а если отрицательно – тупой. В частности, скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны (ортогональны)
R |
Û |
R |
^ b . |
< a,b > = 0 |
a |
Из определения скалярного произведения следует коммутативность этой операции
R |
R |
> , |
< a,b > = < b,a |
||
а из свойств проекций векторов вытекают следующие ее свойства:
R |
R |
R |
R |
R |
R |
< ka,b > = < a, kb > = |
k× < a,b >, |
< a,b + c |
> = < a,b |
||
Докажем последнее из них
> + < R R > a,c .
R |
R |
> = |
R |
|
|
R R |
< a,b + c |
| a |
| (ПрaR (b + c) =| a |
||||
|
R |
|
|
R |
R |
R |
|
| a | ПрaRb +| a | ПрaRc |
=< a,b |
||||
Пр + Пр R =
| ( aRb aRc)
> + < R R > a,c .
Интересно отметить, что скалярное произведение вектора на себя дает
R R |
R |
R |
R |
|2 , |
< a, a |
> = | a |
| ×| a |
| cos 0O =| a |
поэтому модуль вектора выражается через скалярное произведение следующим образом
R |
|
= |
R R |
> . |
(7.1) |
|
|||||
a |
|
< a, a |
Пример. В параллелограмме ABCD одна из сторон вдвое больше другой и острый угол между ними равен 600 . Найти острый угол между диагоналями параллелограмма и проекцию малой диагонали на большую.
49
