9716

[Введите текст]

где при вычислении интеграла суммы нескольких функций сумма произвольных постоянных, которая при этом получается, заменена одной постоянной.

Следует отметить, что некоторые интегралы не могут быть выражены через элементарные функции. В частности, это касается интегралов следующих функций:

29.2. Интегрирование методами подстановки и замены перемен-

ной. Еще одно важное свойство неопределенного интеграла, основанное на инвариантности формы первого дифференциала, позволяет находить интегралы функций, не входящих в таблицу.

Пусть

∫f (x) dx = F(x) + C

иформально подставим в эту формулу функцию x = ϕ(t) , производная которой непрерывна. Тогда получим так называемую формулу подстановки

Покажем, что формула (29.1), действительно, верна. Для этого найдём производную по переменной t правой части этого выражения

Fx′(ϕ(t))ϕ′(t) = f (ϕ(t))ϕ′(t) .

Таким образом, правая часть в (29.1) является первообразной подынтегрального выражения слева.

Применение этой формулы позволяет находить интегралы сложных функций, используя таблицу основных интегралов. Например, найдем

∫cos(3x + 2)dx .

Зная, что

∫cosudu = sinu + C

и делая в этой формуле подстановку u = 3x + 2, получим

211

[Введите текст]

∫cos(3x + 2)d(3x + 2) = sin(3x + 2) + C ,

откуда найдем

∫cos(3x + 2)dx = 1 sin(3x + 2) + C . 3

Этот прием, основанный на подстановке некоторой функции в готовую формулу табличного интеграла, называют методом подстановки.

Рассмотрим теперь приём интегрирования с помощью замены пе-

ременной. Предположим, что нужно найти интеграл ∫ f (x)dx . Заменяем

переменную интегрирования некоторой дифференцируемой функцией x = ϕ(t) , имеющей обратную функцию t = ψ( x) . Предположим также, что

ϕ′(t) непрерывна. Тогда справедлива формула замены переменной в не-

определенном интеграле

подстановки правая часть этого выражения равна

∫ f (ϕ(t))ϕ′(t)dt = F(ϕ(t)) + C = F(x) + C

при x = ϕ(t ) , что подтверждает справедливость формулы (29.2).

Прием замены переменной состоит в том, чтобы после её проведения сделать такую замену, при которой для подынтегральной функции в полученном интеграле справа в (29.2) легко может быть найдена первообразная.

Например, для нахождения интеграла∫ a2 − x2 dx сделаем замену пе-

ременной x = asint так, что

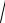a2 − x2 = 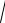a2 − a2 sin2 t = acost , dx = a cos t dt .

Следовательно,

[Введите текст]

Перейдём от переменной t к переменной x . В промежутке −a ≤ x ≤ a

существует обратная функция t = arcsin x , поэтому a

Заметим в заключение этой темы, что в некоторых случаях замену переменной непосредственно не осуществляют, а применяют так называе-

∫ f (ϕ(x))dϕ(x) = ∫ f (ϕ)dϕ.

213

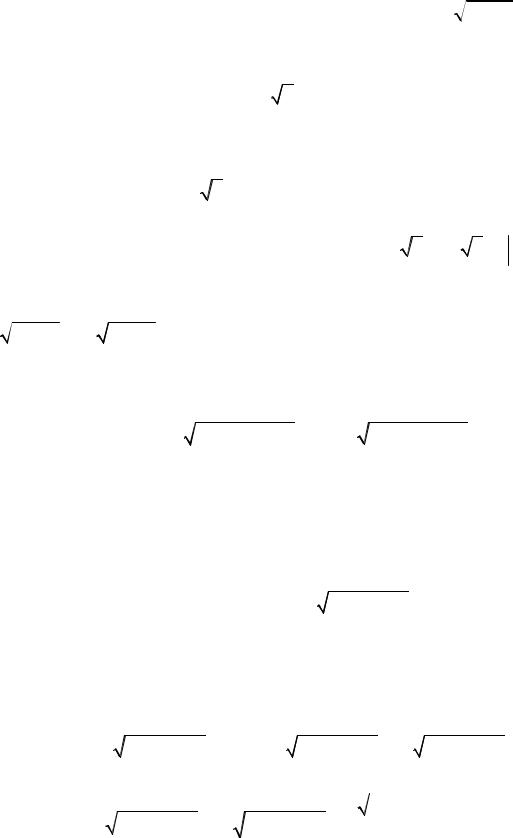
[Введите текст]

Лекция 30. Методы интегрирования (продолжение)

30.1. Интегрирование простейших иррациональностей. Рассмот-

рим только простейшие случаи иррациональных подынтегральных функ-

ций. Если интеграл содержит иррациональность вида n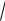ax + b (a ¹ 0) , то применяют подстановку ax + b = tn .

Если подынтегральное выражение содержит иррациональности вида n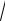ax + b и m ax + b , где m ¹ n , то применяют подстановку ax + b = t p с p ,

Первый из них сводится к табличному интегралу выделением полного квадрата в подкоренном выражении. Для нахождения второго интеграла следует в числителе выделить дифференциал квадратного трехчлена d ( Ax2 + Bx + C) = (2 Ax + B)dx .

В числителе дроби получим дифференциал подкоренного выражения d (3 + 2x - x2 ) = (2 - 2x)dx и разобьём интеграл на два интеграла

[Введите текст]

В интегралах вида

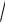∫ a2 - x2 dx , ∫ 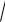a2 + x2 dx , ∫ 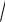x2 - a2 dx

освобождаются от иррациональности применением тригонометрических подстановок. Для первого интеграла применяется замена x = a sin t (можно

ния, который позволит нахождение одного интеграла заменить отысканием другого, «более простого». В основу этого метода положено следующее рассуждение. Пусть u ( x) и v( x) – две функции, имеющие непрерывные производные на некотором интервале. Найдем дифференциал d (u × v) от произведения этих функций

u( x) dv( x) = d (u( x) × v( x)) - v( x)du( x)

и проинтегрируем обе его части. Учитывая, что ∫ d (u × v) = u × v , получим

формулу интегрирования по частям

∫u(x) × dv(x) = u(x) × v(x) - ∫v(x) × du(x) .

Метод интегрирования по частям состоит в представлении интеграла

∫ f (x)dx

в виде ∫u(x) dv(x) так, чтобы интеграл ∫v(x) du(x) в правой части форму-

лы интегрирования по частям оказался «более простым». При нахождении функции v( x) можно произвольную постоянную C , возникающую при этом интегрировании, положить равной нулю.

Найдем интеграл ∫ x ×e− xdx . Введем обозначения: u( x) = x ,

215

тегрального выражения на два множителя u ( x) и dv( x) , причем при переходе к правой части первый дифференцируется, а второй интегрируется. Нужно стараться, во-первых, чтобы интегрирование дифференциала dv не представляло трудностей и, во-вторых, чтобы интеграл ∫v(x) du(x) имел более простое подынтегральное выражение. Так, в предыдущем примере

мы получили более сложный интеграл, чем первоначально данный. Заметим, что если мы имеем интегралы вида

∫Pn (x)sin kxdx , ∫ Pn (x)cos kxdx , ∫ Pn (x)ekxdx ,

( Pn ( x) – многочлен n -ой степени), то следует выбрать u(x) = Pn (x) . При

этом интегрирование по частям проводится столько раз, какова степень многочлена Pn ( x) . Если же имеем интегралы вида

∫ Pn (x)arcsin kx dx , ∫Pn (x)arccos kxdx , ∫ Pn (x)arctg kx dx ,

216

[Введите текст]

30.3. Интегрирование выражений, содержащих тригонометриче-

ские функции. Разнообразие тригонометрических функций и особенно формул, их связывающих, приводит к большому выбору методов вычисления интегралов, содержащих тригонометрические функции. Рассмотрим некоторые из этих методов интегрирования.

Для нахождения интегралов вида ∫sin axcosbxdx , ∫sin axsinbx dx ,

∫cosα xcos β xdx , где α , β – действительные числа, следует преобразовать произведения тригонометрических функций в суммы по формулам

sin ax × cosbx = 12 (sin (a - b) x + sin (a + b) x) , sin ax × sin bx = 12 (cos(a - b) x - cos (a + b) x), cos ax × cosbx = 12 (cos (a - b) x + cos(a + b) x) .

Рассмотрим несколько случаев нахождения интегралов вида

∫sinα xcosβ x dx

взависимости от различных значений чисел α и β . Если хотя бы одно из чисел α или β – положительное целое нечетное число, то поступают

следующим образом: отделяют от тригонометрической функции в нечетной степени функцию в первой степени и вносят ее под знак дифференциала. Оставшуюся четную степень тригонометрической функции преобразуют с использованием формулы sin 2 x + cos2 x = 1 .

[Введите текст]

Если α и β – четные неотрицательные числа, то степени синуса и косинуса понижаются посредством перехода к двойному аргументу с помощью формул:

[Введите текст]

Интеграл вида ∫ R(sin x,cos x) dx , где R(sin x, cos x) – рациональная

функция синуса и косинуса, можно привести к интегралу рациональной дроби (правильной или неправильной) с помощью универсальной триго-

нометрической подстановки

Заметим, что применение универсальной подстановки часто приводит к достаточно громоздким выражениям, поэтому использовать ее нужно только после того, как исчерпаны другие возможности.

219