2. 3. Закон сохранения импульса. @

Рассмотрим общий случай - систему n взаи­модействующих материальных точек (тел). На каждое тело действуют внутренние и внешние силы. Силы взаимодействия между телами системы называются внутрен­ними, а силы, которые действуют со стороны тел, не входящих в рассматриваемую систему, называются внешними. Массы точек - m₁, m₂, ..., m_n, скорости их движения - v₁, v₂,...,v_n. Пусть - внутренние силы, действующие на первую точку со стороны второй, третьей и т.д.- внешние силы, действующие на пер­вую, вторую и т.д. материальные точки (рис.2.3.).

Так как внутренние силы являются силами взаимодействия между телами, то они должны подчиняться третьему закону Ньютона .

Рис.2.3. Силы взаимодействия в системе n материальных точек.

Запишем II закон Ньютона для каж­дого из n тел:

. . . . . .

.

Если просуммировать эти уравнения по всем телам и учесть, что при двойном суммировании внутренних сил, согласно третьему закону Ньютона

, то получаем , где,.

Если система замкнутая, т.е. на нее не действуют внешние силы, то ,, т.е..

Это выражение является законом сохранения импульса. Суммарный импульс замкнутой системы точек (тел) не меняется с течением вре­мени.

Закон сохранения импульса находит широкое применение в природе и техни­ке. Примером может служить явление отдачи ружья при выстреле пули. Выстрел производится в горизонтальном направ­лении (рис.2.4).

Рис.2.4. Применение закона сохранения импульса к стрельбе из ружья.

Систему ружье-пуля можно считать изолированной системой и к ней приме­ним закон сохранения импульса: ,m и v – масса и скорость пули, M и v₀ – масса и скорость ружья. В начальный момент времени (до выстрела) система покоилась (v=v₀=0), следовательно кон­стан­та в уравнении равна нулю. Отсюда, соотношение скоростей v и v₀ после выстрела, можно рассчитать из равенства , .

Т.к. mM, то v>>v₀; знак «минус» указывает на противоположную направленность скоростей. Эксперименты доказывают, что закон сохранения импульса выполняется и для замкнутых систем микрочастиц, т.е. в квантовой механике. Таким образом, закон сохранения импульса универсален и является фунда­ментальным законом природы.

2. 4. Центр масс. Закон движения центра масс. @

Центр масс (или центр инерции) системы материальных точек (тел) есть некоторая точка в пространстве С, положение которой характеризует распределение масс сис­темы. Ее радиус-вектор равен : 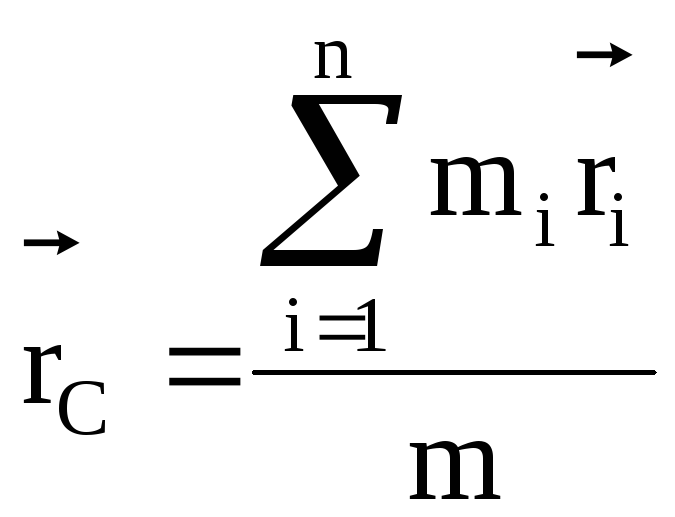, гдеn – число точек (тел) системы, m₁, m₂…m_n – их массы; - их радиусы-векторы;m – общая масса систе­мы. Ско­рость центра масс

. Так как ,- импульс всей системы, тоили импульс системыравен произведению массы системы на скорость ее центра масс.

По II за­кону Ньютона . Отсюда, т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на нее действует сила, равная геометрической сумме всех внешних сил, действующих на тела системы. Это есть закон движения центра масс. Если система замкнута, то,и.

Следовательно центр масс замкнутой системы движется прямолинейно и рав­номерно, либо остается неподвижным. Например, молоток вращается, а его центр масс движется прямолинейно и равномерно (рис.2.5).

Рис.2.5. Свободно летящий молоток. Его центр инерции помечен крестиком.