
Методичка по подготовке к лабораторным работам
.pdfмагнитный поток, что приводит к большим вихревым токам и большему рассеянию потока.
На практике мощность потерь на гистерезис и вихревые токи определяются эмпирическими формулами:
Рг= σг·f· Bnm·G ; Рв= σв·f2 •B2m·G
где σг , σв -коэффициенты , f - частота, Bm – амплитуда магнитной индукции, G-масса сердечника, γ –электропроводность сердечника. Показатель n лежит в интервале 1<n<2. Поэтому с увеличением тока R0 и Xd будут расти. Это приведет к небольшому увеличению полного сопротивления и подьему графика Z=F(I) в области больших токов (рис.17, линия b).
Вопрос 4 . Как уменьшить потери энергии на гистерезис и вихревые токи?
Ответ 4. Для уменьшения потерь на гистерезис магнитопровод изготавливают из материалов с узкой петлей гистерезиса.
Переменный ток катушки создает в магнитопроводе изменяющийся магнитный поток. Магнитный поток направлен вдоль оси катушки. Так как магнитпровод является замкнутым электропроводником, то в переменном магнитном поле, в нем (согласно закону электромагнитной индукции) возникает переменная ЭДС и, соответственно, переменный ток. Этот ток согласно закону Джоуля-Ленца и нагревает магнитпровод. Для уменьшения потерь на вихревые токи магнитопровод изготавливают из набора тонких изолированных друг друга пластин и в состав стали вводят кремний 0,4-5%. Вихревые магнитные поля соседних пластин уничтожают друг друга.
Вопрос 5 . Нарисовать и объяснить схему замещения катушки с сердечником.
Ответ 5. Схема замещения реальной катушки с сердечником представлена на рис.18. Она состоит из 4-х последовательно соединенных элементов: активного сопротивления обмотки катушки R, индуктивного сопротивления рассеяния xd , индуктивного сопротивления x0 , обусловленного основным магнитным потоком, замыкающимся по стальному сердечнику и активным сопротивлением R0, учитывающим потери в сердечнике (потери от вихревых токов и потери на перемагничивание сердечника при наличии гистерезиса).
31
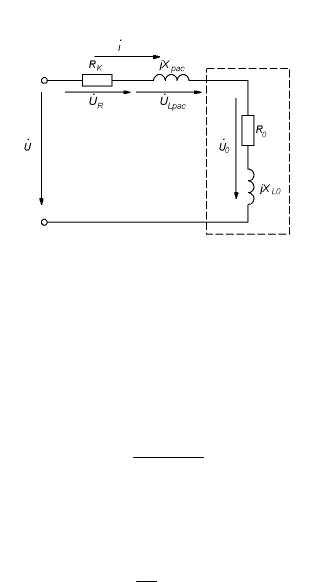
Индуктивное сопротивление ХL0=ω·L0=ω·μr·L00, где L00 – индуктивность катушки без сердечника, μr относительная магнитная проницаемость. Магнитная проницаемость μr в ферромагнетиках сильно зависит от напряженности магнитного поля катушки, а, следовательно, и от тока в катушке. Это нелинейный элемент. Однако в случае отсутствия гистерезиса можно считать μr =const.
В этом случае уравнение электрического состояния катушки с сердечником можно представить в комплексной форме:
U E RI jxd I
где É- комплекс эдс самоиндукции.
Вопрос 6. Как определяются параметры схемы замещения и зависят ли они от подводимого напряжения?
Рис.18 Ответ 6 Параметры этой схемы замещения определяются по
следующим формулам: а) полное сопротивление катушки с сердечником, Ом:
Z U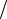 I ,
I ,
где U - приложенное напряжение, В: I - ток в цепи, А; б) общее активное сопротивление цепи, Ом:
R R0 (Pэ I2Pм )
где Pэ - электрические потери, Вт, Pм - магнитные потери (потери в сердечнике), Вт;
в) активное сопротивление обмотки катушки, Ом:
R Pэ ,
I2
32
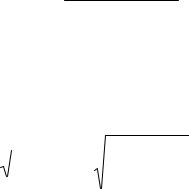
(величина R указана на исследуемой катушке);
г) общее реактивное сопротивление катушки с сердечником, Ом,
xd x0 
 Z2 (R R0)2
Z2 (R R0)2
где xd - индуктивное сопротивление, обусловленное потоком рассеяния;
д) индуктивное сопротивление, обусловленное основным магнитным потоком, Ом,
|
|
|
|
|
|
|
E |
2 |
, |
|
|
|
|
|
|
|
|||||
x |
0 |
|
Z2 |
R2 |
|
|
|
|
R2 |
|
|
||||||||||
|
|
0 |
0 |
|
|
I |
0 |
|
||
|
|
|
|
|
|
|
|
|||
Е - рассчитывается по формуле трансформаторной эдс:
Е=4.44·w·f·Фm
где Фm-амплитуда магнитного потока. Фm определяется по калибровочному (экспериментальному графику Фm=f(I).
Активная мощность, потребляемая катушкой с сердечником, расходуется на покрытие электрических потерь в обмотке катушки и магнитных потерь в стальном сердечнике (измеряется ваттметром
РW):
P Pэ Pм RI2 R0I2 UIcos .
Отсюда активная мощность, идущая на покрытие магнитных потерь, определяется уравнением:
P P P P RI2 , |
|
|
м |
э |
|
а реактивная мощность рассчитывается по формуле: |
|
|
Q xd I2 |
x0I2 UIsin . |
|
Вопрос 7. Объяснить характер зависимостей I(U); Z(I); |
Ia (U); |
|
Iм (U). |
|
|
Ответ 7-1 Зависимость Z= f(I) |
|
|
Если пренебречь индуктивностью рассеяния и магнитными |
||
потерями, то полное сопротивление катушки приближенно |
равно |
|
Ż=Rк+j·XL0. Индуктивное сопротивление XL0=ω·L0=ω·μr·L00, где L00
– индуктивность катушки без сердечника, |
μr относительная |
магнитная проницаемость. Магнитная |
проницаемость μr в |
ферромагнетиках сильно зависит от напряженности магнитного поля катушки, а следовательно и от тока в катушке. Зависимость μr от тока I . представлена на рис. 19.
33
RK не зависит от тока. Обычно XL>> RK, поэтому зависимость сопротивления Z= f(I) близка к зависимости μr= f(I) (рис. 19, линия a).
Область резкого нарастания |
μ, Z |
|
Z от тока очень узкая и |
|
|
часто экспериментально не |
b |
|
измеряется. |
a |
I |
Учет потерь приводит к |
μ |
|
|
|
|
увеличению доли активного |
Рис. 19 |
|
сопротивления в цепи, но незначительно изменит характер зависимости полного сопротивления от тока (рис. 19, линия b).
**)При выполнении лабораторной работы начальную область резкого нарастания Z от тока исследователь не видит.
Ответ 7-2 |
Зависимость U=f(I) |
-это вольтамперная |
характеристика |
катушки с сердечником. |
Экспериментальная |
кривая U= f(I) представлена на рис.20. |
|
|
U, Z |
UL(I |
|
|
Z |
|
|
I |
|
Рис. 20
Вариант ответа a) По закону Ома U =I· Z . При линейном возрастании тока и постоянном Z падение напряжения U должно нарастать также линейно. Однако в нашем случае сопротивление Z само зависит от протекающего через него тока Z=f(I). Поэтому график U=f(I)= I·Z(I) это произведение линейной функции и нелинейной функции Z=f(I) (рис.21).
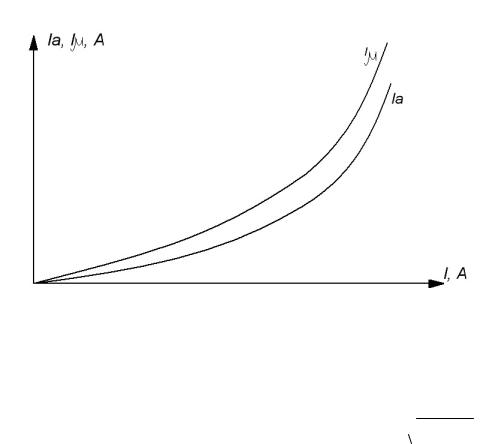
Ответ 7.3 График зависимости Ia=f(I)
Объяснение. График строиться на анализе формулы: Ia Pм
E
34
Магнитные потери Рм состоят из двух видов потерь: на перемагничивание сердечника и на вихревые токи. Оба вида потерь зависят от тока и описываются эмпирическими формулами:
Рг= σг·f·Bnm·G ; Рв= σв·f2·B2m·G
где σг , σв - коэффициенты, f -частота, Bm – амплитуда магнитной
индукции, |
G-масса, γ –электропроводность сердечника. |
Показатель n |
лежит в интервале 1,6<n<2. Амплитуда магнитной |
индукции Bm |
зависит от тока также как и амплитуда магнитного |
потока Фм. Т.к потери на вихревые токи пропорциональны квадрату
тока I2м, а зависимость ЭДС Е |
от тока I известна Е (I) ≈ Фm(I), то |
Iа будет расти согласно |
отношению Ia≈const· I2/Фм (I). На |
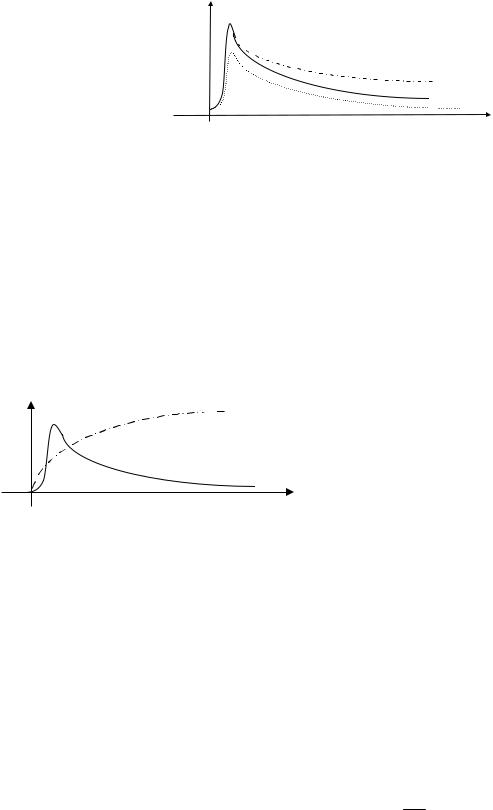
начальном участке линейно, затем квадратично. График Ia=f(I) представлен на рис. 21.
Рис. 21
Ответ 7.4 График зависимости Iμ=f(U)
График cтроится на анализе формулы: I 
 I2 Ia2 . График Ia=f(I)
I2 Ia2 . График Ia=f(I)
показан на рис.21.
Рост полного тока I идет быстрее роста активной части полного тока Ia, поэтому магнитная составляющая полного тока Iμ растет с увеличением полного тока. График Iμ=f(U) представлен на рис.21.
35
Тема № 4: ИССЛЕДОВАНИЕ ОДНОФАЗНОГО ТРАНСФОРМАТОРА
Цель работы: 1) ознакомиться с устройством и принципом действия однофазного трансформатора;
2) изучить режимы работы и методику опытного определения основных параметров трансформаторов.
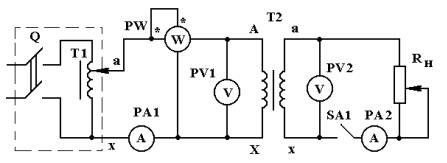
Работа выполняется на универсальном стенде, где установлены лабораторный автотрансформатор Т1, измерительные приборы, однофазный двухобмоточный трансформатор Т2, реостат Rн . Электрическая схема стенда представлена на рис.26.
Рис. 22
Контрольные вопросы
Вопрос 1. Устройство и принцип действия трансформатора. Ответ 1. Трансформатор – это статическое электромагнитное
устройство, предназначенное для преобразования переменного тока одного напряжения в переменный ток другого напряжения, но той же частоты.
Основными конструктивными элементами трансформатора являются магнитопровод и обмотки. Магнитопровод служит для усиления основного магнитного потока и обеспечения магнитной связи между обмотками.
В работе рассматривается двухобмоточный силовой трансформатор (рис.23).
36
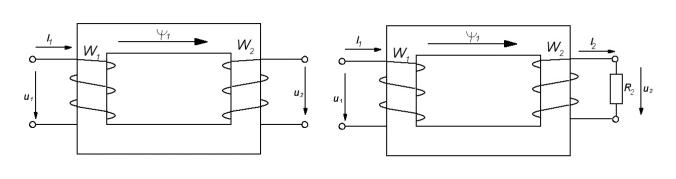
Рис. 23 |
|
|
|
Рис. 24 |
|
К первичной обмотке |
W1 |
подводится электрическая энергия от |
|||
источника. От вторичной обмотки W2 |
энергия |
отводится к |
|||
приемнику (потребителю). |
|
|
|
|
|
Под действием переменного |
напряжения |
u1 (t) |
в первичной |
||
обмотке возникает ток |
i1 |
(t) |
и в сердечнике |
возбуждается |
|
изменяющийся магнитный поток w1·ф(t). Этот поток индуцирует
эдс е1(t) и е2(t) в обеих обмотках трансформатора. |
ЭДС е1 |
уравновешивает основную часть напряжения u1 , а е2 |
создает |
напряжение u2 на выходных клеммах трансформатора. При включении нагрузки во вторичной обмотке в цепи нагрузки возникает ток i2(t), который создает собственный магнитный поток, накладывающийся на магнитный поток от первичной обмотки. В результате создается общий магнитный поток сердечника Ψ, сцепленный с витками обеих обмоток трансформатора и определяющий в них результирующие ЭДС е1 и е2 с действующими значениями: E1 4.44W1 fФm и E2 4.44W2 fФm , где Фm - амплитуда магнитного потока: f - частота переменного тока;
W1, W2 |
- число витков обмоток. |
|
|
На |
щитке |
трансформатора указываются его |
номинальные |
напряжения - |
высшее (ВН) и низшее НН) . Так же |
указываются |
|
номинальная |
полная мощность S (ВА), токи (А) , число фаз, схема |
||
соединения, режим работы, и способ охлаждения. |
|
||
Вопрос 2. Записать и объяснить формулы ЭДС и уравнения электрического и магнитного состояний трансформатора Ответ 2-1 ЭДС определяется скоростью изменения магнитного
потока сердечника и числом витков w1 , w2 обмоток трансформатора
37
Впервичной обмотке под действием напряжения U1 возникает ток I1. Он создает магнитный поток катушки с сердечником. Поток переменный, он наводит в первичной обмотке ЭДС самоиндукции e1 = - w1dФ/dt, а во вторичной обмотке ЭДС взаимоиндукции
е2= - w2dФ/dt. Магнитный поток для обоих обмоток один и тот
же.
Врежиме холостого хода катушка - чистая индуктивность,
поэтому если напряжение изменяется по закону u1(t) =U1m·sinωt , то ток отстает от напряжения на 90°:
i(t) =I1m Sin(ωt-90°), магнитный поток совпадает по фазе с током Ф(t) =Ф1m·sin(ωt-90°). Тогда ЭДС будут равны
е1 = - w1dФ/dt = -w1ω Ф1m·sin ωt= -E1m·sinωt е2 = - w2dФ/dt = -w2ω Ф1m·sin ωt= -E2m·sinωt
Векторная диаграмма идеального (без потерь) трансформатора в режиме холостого хода представлена на рис.25:
U1
I1xx Ф1хх
U2 |
E2 |
|
|
E1 |
|
|
Рис. 25 |
|
Ответ 2-2. Уравнения |
электрического состояния |
реального |
трансформатора для первичной и вторичной цепей имеют вид:
U1 E1 R1I jx1d I1; U2 E2 R2I jx2d I2 ,
где R1 и R2 – активные сопротивления обмоток; x1d и x2d – индуктивные сопротивления рассеяния обмоток.
Ответ 2-3. Уравнения магнитного состояния трансформатора можно получить, исходя из анализа МДС в трансформаторе. ЭДС обеих обмоток возникают благодаря изменению одного и того же магнитного потока Ф с индукцией В. Индукция В и напряженность магнитного поля H связаны зависимостью B=μ·H. Пусть μ=const.
38
Напряженность магнитного поля H по закону полного тока связана с суммарной МДС обеих обмоток соотношением :
Н·l = I1 ·w1+(-I2) ·w2,
где l - длина средней линии магнитопровода; I1 ·w1 - МДС первичной обмотки;
-I2 ·w2 - МДС вторичной обмотки. Знак минус МДС вторичной
обмотки отрицательный |
в силу закона ЭМИ (правило Ленца –ток |
||
возникающий в обмотке |
2 всегда будет иметь направление, |
при |
|
котором магнитный поток, создаваемый |
током I2, |
будет |
|
препятствовать изменению основного потока)
ЭДС Е1=const·Ф= const·В·S= const·μ·H·S, Е1 = const·μ ·( I1 ·w1-I2 ·w2) ·S/ l
В режиме холостого хода I2=0, соответственно, уравнение (5-3) будет иметь вид:
Е1=const·μ·I10·w1·S/ l
где I10 ток первичной обмотки трансформатора в режиме холостого хода.
Из уравнений и получим уравнение магнитного состояния трансформатора:
w1I1 w1I10 w2I2
Определим ток I1:
I1= I10 - Iי2
где I10 – ток холостого хода или намагничивающий ток (ток создающий магнитный поток )
Iי2= - w2/w1·I2 - компенсирующий ток. Tок Iי2 компенсирует действие тока вторичной обмотки на основной магнитный поток.
Магнитный поток в сердечнике всегда постоянный.
Вопрос 3. Что такое «коэффициент трансформации»?
Ответ 3. Согласно второму закону Кирхгофа уравнения электрического состояния идеализированного трансформатора имеют вид:
U1= -Е1 , |
U2=Е2 |
Е1= -w1dФ/dt , |
Е2= -w2dФ/dt . |
Поделив U1 на U2 получим коэффициент трансформации n:
39
U1 E1 w1 n, U2 E2 w2
В случае реального трансформатора напряжение U2 совпадает c эдс E2 только при холостом ходе. Поэтому коэффициент
трансформации n U1 w1 .
U20 w2
где U20 – напряжение на зажимах вторичной обмотки в режиме холостого хода.
Вопрос 4. Нарисовать и объяснить схему замещения нагруженного трансформатора.
Ответ 4. В режиме холостого хода схема замещения трансформатора совпадает со схемой замещения катушки индуктивности (рис.18).
В режиме нагрузки трансформатора ( при отсутствии гистерезиса) электрическое состояние трансформатора можно описать (на основании 2-го закона Кирхгофа) комплексными уравнениями:
|
, |
|
|
|
|
|
1 2 1xx , |
|
|
|
|
||
|
|
|
||||
U1 |
E1 R1 I jx1pac I1 |
E1 I 1Zob1 |
||||
|
. |
, |
|
, , |
|
, , , |
U2 |
E2 R2 |
I2 jx2 pac I2 |
E2 I2 Zob2 |
|||
|
, , |
, |
|
|
|
|
U2 |
I2 Z2, |
|
|
|
|
|
где: R1 –активное сопротивление 1-ой обмотки,
R’2 =(w1/w2)2 R2 – приведенное активное сопротивление вторичной обмотки, Ż об1 – комплексные сопротивление 1-ой обмотки,
x рас1 =ωLрас1 – сопротивление рассеяния первичной обмотки,. x’рас2 =ωL’рас2 =(w1/w2)2 · ωLрас2 – приведенное сопротивление рассеивания вторичной обмотки , Ż‛об2 – приведенное комплексное сопротивление 2-ой обмотки, Ż’об2 = R’2 + jx’рас2 ,
Ż‛2 – приведенное комплексное сопротивление нагрузки
Ż’2=(w1/w2 )2 ·Ż2
40
