
Методичка по подготовке к лабораторным работам
.pdf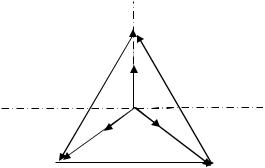
120° соответственно. Концы векторов обозначаем малыми буквами b и c соответственно.
4. Точку, соответствующую началу координат, обозначим малой буквой n. Это точка нейтрали приемника.
5.Строим вектора линейных напряжений. Для этого соединяем концы фазных векторов. Получим вектора Uab= UAB, Ubc= UBC, Ucа= UCА. Отметим, что линейные напряжения приемника равны линейным напряжениям генератора.
Точка N на векторной диаграмме, соответствующая нейтральной точке генератора, находится в центре треугольника линейных напряжений. В данном случае нейтраль генератора N совпадает с нетралью приемника n. В общем случае точку n, соответствующую нейтральной точке нагрузки, находят методом засечек. Векторы токов откладывают по отношению к соответствующим векторам фазных напряжений с учетом сдвига фаз между ними.
Ниже приведены векторные диаграммы для различных режимов
работы. |
|
|
|
|
Режим 1. Равномерная нагрузка |
без |
нейтрального провода |
||
(рис. 8). |
|
|
|
|
|
+1 |
а |
|
|
|
|
|
|
|
|
UAB |
Ua |
|
|
+j |
N |
Ia |
UСA |
|
|
n |
|
|
|
|
Ib |
|
Ic |
|
b |
Ub |
|
Uc |
с |
|
UBC |
|
|
|
Рис. 8
Режим 2. Обрыв фазы А ( рис. 9):
При обрыве фазы А и одинаковой нагрузке двух других фаз,
нейтральная точка приемника |
n |
переместится |
на середину |
|
линейного напряжения ŮBC .Сопротивления Zb и Zc |
окажутся |
|||
соединенными последовательно |
и |
включенными |
на |
линейное |
напряжение U BC. Падение напряжения между точками А и n
21
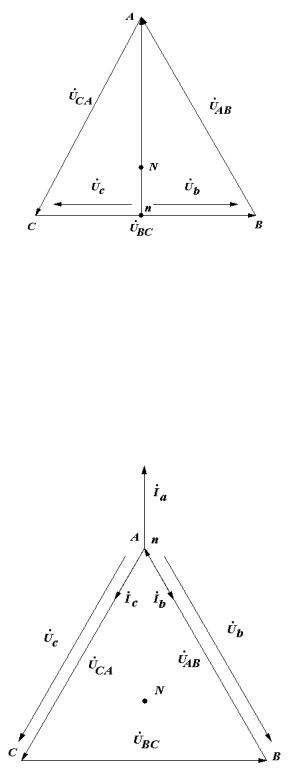
увеличится, а фазные напряжения U b и |
U c станут равными |
половине линейного U BC. |
|
Рис. 9
Режим 3. Короткое замыкание фазы А (рис. 9).
При замыкании фазы А и одинаковой нагрузке двух других фаз (то есть при соединении начала нагрузки фазы А с нулевой точкой нагрузки) точка n перемещается в точку А. Фазное напряжение Ůа становится равным нулю, ток İa увеличивается, а фазные напряжения U b и U c становятся равными линейным.
Рис. 9
Режим 4. Неравномерная нагрузка без нейтрального провода
22
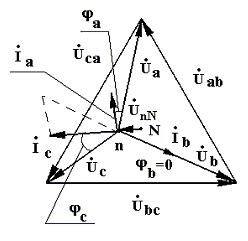
(рис. 10).
Сопротивления, Zа≠Zb≠Zc, фазные напряжения приемника U а ≠U b ≠U c, между точками N и n появляется напряжение смещения нейтрали.
4.1 Вначале строим треугольник линейных напряжений.
4.2. Методом засечек (циркулем или линейкой) из каждой вершины откладываем соответствующие вектора фазных напряжений приемника. Точка пересечения дуг даст точку нейтрали приемника n. Точку нейтрали генератора N оставляем на прежнем месте.
4.3Соединяем точку n и N . Это вектор напряжения смещения нейтрали UnN (в масштабе).
4.4Строим вектора фазных токов нагрузки. В случае, если нагрузкой являются лампочки, которые можно представить как активные сопротивления, то сдвига фаз между фазным напряжением и фазным током нагрузки не будет. Поэтому вектора токов откладываем ( в масштабе) вдоль соответствующих векторов фазных напряжений.
***) В общем случае надо определить сдвиги фаз между током
исоответствующим фазным напряжением по закону Ома в комплексной форме и строить вектор тока с помощью транспортира.
Рис. 10
Режим 5. Неравномерная нагрузка с нейтральным проводом
(рис.11).
23
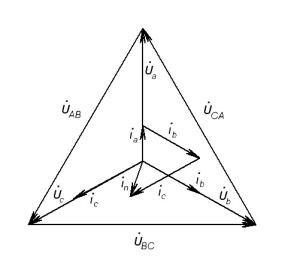
При наличии нейтрального провода фазные напряжения приемника становятся равными фазным напряжениям источника
U A=U а ; U В =U b; U C =U c :
Рис. 11
Вопрос 9. К чему приведет обрыв нейтрального провода при несимметричной нагрузке?
Ответ 9. Обрыв нейтрального провода при несимметричной нагрузке приведет
а) к появлению напряжения смещения нейтрали, б) к неравенству фазных напряжений приемника ( и токов в
фазах нагрузки).
U A≠U а ; U В ≠U b; U C ≠U c
U а ≠U b ≠U c; İa≠ İb≠İc.
Вопрос 10. Как изменяется напряжение при обрыве одной фазы в четырехпроводной и трехпроводной сетях?
Ответ 10 а) При обрыве одной фазы (например обрыв фазы а) в четырехпроводной сети фазные напряжения U а, U b, U C останутся прежними, а ток в нейтральном проводе измениться:
İNn= İb + İc, (Ia=0)
б) При обрыве одной фазы (например обрыв фазы а) в трехпроводной сети фазные токи и напряжения изменятся, при этом независимо от предыдущего состояния цепи токи будут равны:
24

|
|
|
|
|
|
U BC |
|||
Ib IC |
|
|||
|
||||
(Zb ZC )
напряжения будут равны :
U b= İb·Zb ; |
U c |
|
В случае если Zb= Zc, |
то: |
|
U |
b= U c= U BC/2, |
|
= İb·Zc, U а= U А- U Nn
U а= 
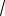 3 3/2 ·U BC=3/2 ·UФ
3 3/2 ·U BC=3/2 ·UФ
Вопрос 11. а) Как изменяется напряжение при коротком замыкании фазы в трехпроводной сети?
б) К чему приведет короткое замыкание фазы в четырехпроводной сети?
Ответ 11.1. .Короткое замыкание фазы (например фазы «а») в трехпроводной сети приведет к:
1)Фазное напряжения Uа =0.
2)При замыкании фазы «а» и одинаковой нагрузки двух других фаз (то есть при соединении начала нагрузки фазы А с нулевой точкой нагрузки) точка n перемещается в точку А (рис. 9). Фазное
напряжение U а становится равным нулю, ток İa увеличивается, а фазные напряжения U b и U c становятся равными линейным. При этом вектора UC и UСА будут параллельны, а вектора Ub и UAB будут направлены встречно, UC =UСА , Ub = -UAB.
Ответ 11.2. Короткое замыкание фазы (например фазы «b») в четырехпроводной сети приведет:
1) К замыканию генератора фазы «b», при этом ток короткого замыкания будет ограничен только внутренним сопротивлением
генератора фазы «В» Z . |
I |
|
|
EB |
и сопротивлением линейного |
|
|
||||
int |
|
b |
|
Zint |
|
инейтрального проводов.
2)Фазное напряжения Ub станет равным 0.
3)Фазные напряжения Uа и Uc нагрузок не изменятся.
Вопрос 12. К чему приводит обрыв линейного провода в трехфазной установке а) четырехпроводной и б) трехпроводной систем?
25
Ответ 12 а) В четырехпроводной системе – к изменению тока в нейтральном проводе. Напряжения не изменяются.
б) В трехпроводной системе при обрыве фазы А сопротивление Zb и Zc окажутся соединенными последовательно и включенными на линейное напряжение ŮBC.
Разность потенциалов между А и n увеличится, а фазные напряжения U b и U c станут равными половине линейного U BC.
Вопрос 13. Как измеряют мощность трехфазной несимметричной нагрузки в четырехпроводной системе?
Ответ 13. В этом случае применяют три однофазных ваттметра, каждый из которых подключается на соответствующее фазное напряжение и соответствующий фазный ток. Активная мощность системы равна алгебраической сумме показаний трех ваттметров (рис.12).
Рис. 12
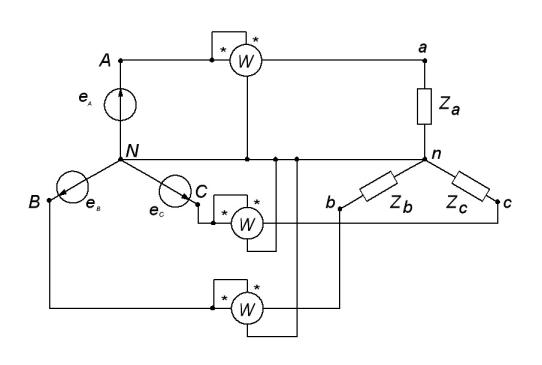
Вопрос 14. В каких случаях используется метод измерения мощности двумя ваттметрами?
Ответ 14. Этот метод применяют при несимметричной нагрузке без нейтрального провода. Сумма показаний двух ваттметров при этом определяет активную мощность всей системы
26
независимо от того, в звезду или треугольник соединена нагрузка.
***)треугольник нагрузки всегда может быть преобразован в эквивалентную звезду.
Рис. 13 Вопрос 15. Написать уравнения для активной, реактивной и
полной мощностей при симметричной и несимметричной нагрузках.
Ответ 15.
Мощность приемников при любом виде нагрузки
Активная мощность приемников в 3-х фазных цепях равна
алгебраической сумме активных мощностей отдельных фаз: Р = РA +РB +РC
Реактивная мощность приемников в 3-х фазных цепях равна
алгебраической сумме реактивных мощностей отдельных фаз: Q = QA +QB +QC
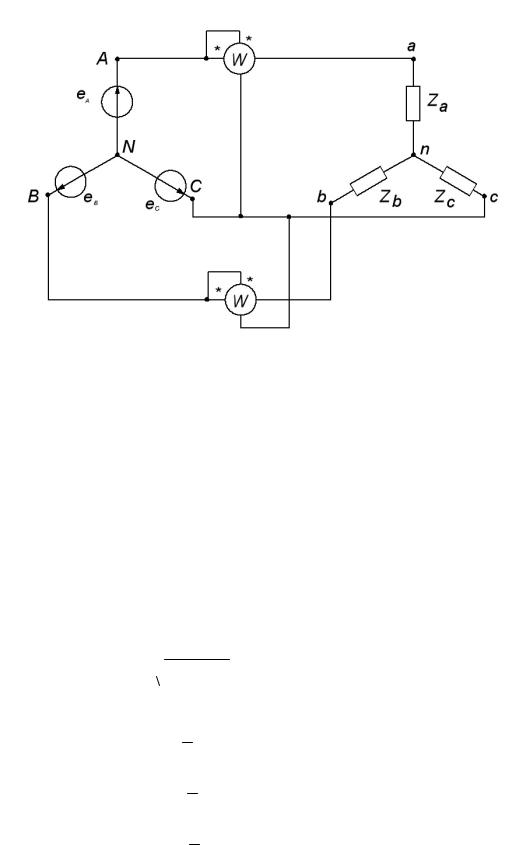
Полная мощность S 
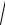 P2 Q2 .
P2 Q2 .
Активная мощность при симметричной нагрузке:
Р = 3·Рф =3·Uф·Iф ·cosφф или Р =
 3·UЛ ·I Л ·cosφф
3·UЛ ·I Л ·cosφф
Реактивная мощность приемников при симметричной нагрузке
Q= 
 3·UЛ IЛ sinφф
3·UЛ IЛ sinφф
Полная мощность приемнико при симметричной нагрузке: S = 
 3·UЛ ·I Л
3·UЛ ·I Л
27
Тема № 3. ИССЛЕДОВАНИЕ КАТУШКИ СО СТАЛЬНЫМ СЕРДЕЧНИКОМ
Цель работы: 1) изучить особенности работы катушки со стальным сердечником в цепях переменного тока;
2)снять вольт - амперную характеристику катушки при подключении ее к источнику переменного тока;
3)определить параметры схемы замещения и построить векторную диаграмму катушки с сердечником.
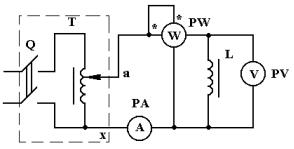
Лабораторная работа проводится на стенде, принципиальная схема которого представлена на рис. 14.
Рис. 14
Исследуемый объект - катушка со стальным сердечником L. Стенд питается от регулируемого источника переменного тока промышленной частоты. Измерительные приборы амперметр -РА, вольтметр- PV, ваттметр-PW.
Контрольные вопросы
Вопрос 1: Где и с какой целью применяют катушки со стальным сердечником?
Ответ1. Катушки индуктивности являются основным источником магнитной энергии. Количественной мерой является магнитодвижущая сила F= I·w, где I- ток через катушку, w-число витков катушки индуктивности. [F]=A·виток.
Катушки со стальным сердечником (магнитопроводом) являются основным элементом различных электрических приборов и электрических машин в промышленности – это статоры и роторы машин, электромагниты – катушки возбуждения двигателей постоянного тока, асинхронных двигателей с фазным ротором,
28
электромагниты |
роторов |
синхронных |
машин, |
катушки |
||
электромагнитных |
реле, датчики |
измерения (эдс, |
магнитного |
|||
потока) или преобразования |
неэлектрических величин |
в |
||||
электрические (датчики перемещения, скорости, ускорения), трансформаторы, магнитные усилители, ограничители переменного тока, фильтры выпрямителей (дроссели).
Катушки со стальным сердечником (магнитопроводом) являются основным элементом различных измерительных электромеханичеких приборов: амперметров, вольтметров, ваттметров электромагнитной и электродинамической систем.
Вопрос 2. С какой целью магнитопроводы электротехнических
устройств изготавливают из ферромагнитных материалов? |
|
Ответ 2. 1. Введение стального сердечника в |
катушку |
увеличивает ее индуктивность согласно формуле:L=μr·L0 |
где μr - |
относительная магнитная проницаемость сердечника, L0- индуктивность катушки без сердечника. Относительная магнитная проницаемость μr ферромагнитных материалов может достигать 104. Т.о. индуктивность L, а следовательно и индуктивное сопротивление ХL= ω·L = μr·ω·L0 возрастет в μr раз.
2. Введение стального сердечника в катушку увеличивает магнитную индукцию В в катушке (сердечнике) также в μr раз.
***) Если сравнить силу притяжения якоря в 2-х электромагнитных реле, изготовленных со стальным сердечником в катушке и без сердечника, то сила притяжения якоря в катушке со стальным сердечником будет значительно (~ в μr раз) больше. Т.к. согласно закону Ампера сила магнитного взаимодействия пропорциональна индукции магнитного поля
F=BIi.
Вопрос 3. Объяснить характер изменения индуктивного и полного сопротивления катушки с сердечником от протекающего через неe тока.
Ответ 3.
****) Индуктивностью называется величина равная отношению магнитного потока катушки ψ= nФ к току катушки
L= ψ/I.
Схема замещения реальной катушки с сердечником представлена на рис.15 и рис.16. На схеме рис.15 она состоит из 4-
29
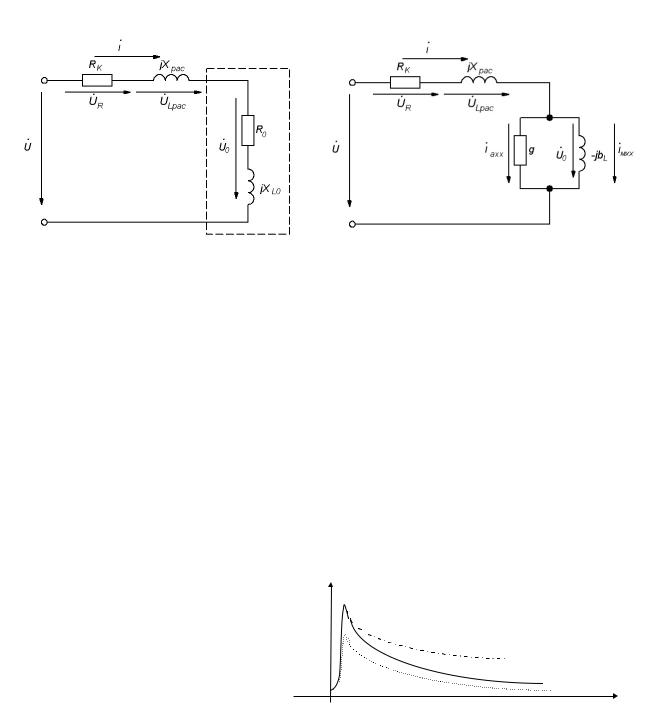
х последовательно соединенных элементов: активного сопротивления обмотки катушки RК, индуктивного сопротивления рассеяния xd , индуктивного сопротивления XL0, обусловленного основным магнитным потоком, замыкающимся по стальному сердечнику и активным сопротивлением R0, учитывающим потери в сердечнике (потери от вихревых токов и потери на перемагничивание сердечника при наличии гистерезиса).
Рис. 15 Рис. 16
Если пренебречь индуктивностью рассеивания и магнитными потерями, то полное сопротивление катушки приближенно равно Ż=Rк+j·XL0. Индуктивное сопротивление XL0=ω·L0=ω·μr·L00, где L00
– индуктивность катушки без сердечника, μr относительная магнитная проницаемость сердечника. Магнитная проницаемость μr в ферромагнетиках сильно зависит от напряженности магнитного поля катушки, а, следовательно, и от тока катушки. Зависимость μr от тока I представлена на рис. 17.
RK не зависит от |
тока. Обычно XL>> RK, поэтому зависимость |
|||||
сопротивления |
Z= |
f(I) |
близка к зависимости μr= f(I) (рис.17, |
|||
линия a). |
|
|
|
|
|
|
Если учитывать магнитные |
μ ,Z |
|
||||
потери, |
то |
необходимо |
|
|
||
рассмотреть |
зависимость |
b |
|
|||
сопротивления потерь R0 |
и |
a |
I |
|||
индуктивности |
рассеяния |
μ |
|
|||
Xd от |
тока в |
катушке. С |
Рис. 17 |
|
||
увеличением тока растет и
30
