Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Справочные сведения по дисциплине СМ ()

.pdf

Скачиваний:

Добавлен:

12.03.2015

Размер:

586.7 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Нормальные линейные размеры по ГОСТ 6636, мм

Rа40: 1; 1,05; 1,1;

1,15;

1,2; 1,3;

1,4;

1,5;

1,6;

1,7;

1,8;

1,9;

2,1;

2,2;

2,4;

2,5;

2,6;

2,8;

3,2;

3,4;

3,6;

3,8;

4,2;

4,5;

4,8;

5,2;

5,5;

6,3;

6,5;

7,5;

8,5;

9,5;

10;

10,5;

11;

11,5;

12;

13;

14;

15;

16;

17;

18;

19;

20;

21;

22;

24;

25;

26;

28;

30;

32;

34;

36;

38;

40;

42;

45;

48;

50;

52;

55;

60;

63;

65;

70;

75;

80;

85;

90;

95;

100;

105;

110;

115;

120;

130;

140;

150;

160;

170;

180;

190;

200;

210;

220;

240;

250.

Кратные и дольные единицы системы СИ

Таблица 10

Приставка

Обозначение

Множитель

Тера

1012

Гига

109

Мега

106

Кило

103

Гекто

102

Деци

10-1

Санти

10-2

Милли

10-3

Микро

мк

10-6

Нано

10-9

Единицы измерения механических величин в Международной системе (СИ)

				Т а б л и ц а 11
Наименование ве-	Наиме-	Обозна-		Соотношения единиц
личин	нование	чения
	единиц
Сила, груз	Ньютон	Н	1	Н = 0,1 кгс
Погонная интен-		Н/м	1	Н/м = 0,1 кгс/м =
сивность нагрузки			= 10-3 кгс/см
Напряжение	Паскаль	Па	1	Па = 1 Н/м2 =
			= 0,1 кгс/м2
Модуль упругости	Паскаль	Па
Интенсивность на-	Паскаль	Па
грузки на поверх-
ность
Момент силы		Н∙м	1	Н∙м = 0,1 кгс∙м =
			= 10 кгс∙см
Работа, энергия	Джоуль	Дж	1	Дж = 1 Н∙м =
			= 0,1 кгс∙м
Мощность	ватт (джо-	Вт	1	Вт = 1 Дж∙с =
	уль		= 0,1 кгс м/с
	в секунду)
Длина	метр	м	1	м = 100 см = 1000 мм
Масса	килограмм	кг	1	кг = 0,001 т
Плотность (удель-		кг/м3
ная масса)
Удельный вес		кгс/м3

Таблица тригонометрических функций

Т а б л и ц а 12

α	sin	cos	tg α
0o	0	1	0
5o	0,0872	0,9962	0,0875
10o	0,1736	0,9848	0,1763
15o	0,2588	0,9659	0,2679
20o	0,3420	0,9397	0,3640
25o	0,4226	0,9063	0,4663
30o	0,5	0,8660	0,5774
35o	0,5736	0,8192	0,7002
40o	0,6428	0,7660	0,8391
45o	0,7071	0,7071	1,0
50o	0,7660	0,6428	1,1918
55o	0,8192	0,5736	1,4281
60o	0,8660	0,5	1,732
65o	0,9063	0,4226	2,145
70o	0,9397	0,3420	2,747
75o	0,9659	0,2588	3,732
80o	0,9848	0,1736	5,671
85o	0,9962	0,0872	11,43
90o	1	0	∞

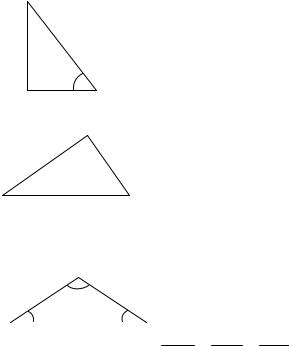
Соотношения для прямоугольного и произвольного треугольников

Для прямоугольного треугольника:

а csin ;

a btg

b ccos ;

b actg

c2 a2

– теорема Пифагора

а, b – катеты; с – гипотенуза; α – угол между

сторонами b, с.

;

b c

аc

ac,bc

– проекции катетов а, b на гипотенузу с.

Для произвольного треугольника:

		а			γ		b
		β					α
						c
a2 b2				c2		2bccos
b2 a2				c2
						2accos
c	2	a	2	b	2	2abcos

a, b, c – стороны треугольника α, β, γ – углы треугольника

sin sin sin – теорема синусов a b c

– теорема косинусов

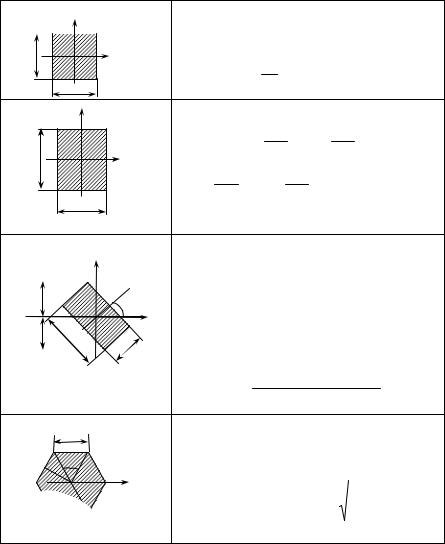
Геометрические характеристики плоских сечений

Т а б л и ц а 13. Сплошные сечения

Квадрат

		у		A a2 ; Ix Iy a4 /12;
а			х
	О			Wx Wy a3 /6;

аix iy a/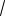12 0,289a

	у			Прямоугольник
	у				bh3			b3h
		A bh; Ix			bh3		; Iy	b3h	;
h	О	A bh; Ix				12	; Iy		;
h	О	х	bh2			12	b2h	12
		W	bh2	W			b2h
		W	;	W			;
	b	x	6		y		6
	b	ix 0,289h;			iy 0,289b.
		ix 0,289h;			iy 0,289b.

Прямоугольник, повернутый на угол α

hcos bsin ;

A bh;

yB yH

α х

bh3

h2 cos2

b2 sin2

;

h О

cos

sin

;

6 hcos bsin

ix 0,289h2 cos2 b2 sin2 .

Правильный n – угольник

na2ctg ; R

; r

;

2sin

2tg

nar

12r2 a2 ; ix

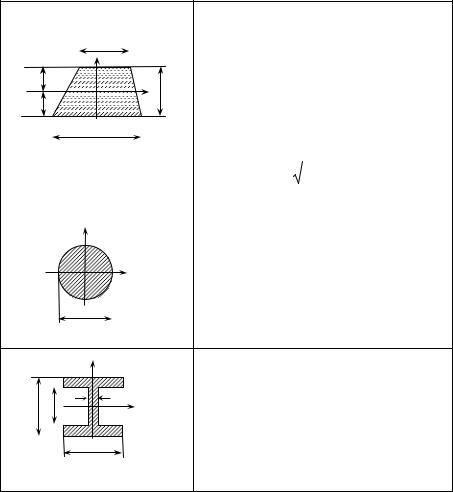
Продолжение таблицы 13

Трапеция

bH 2bB

2bH bB

х h

yH 3 bH bB h; yB

3 bH bB h;

h3 b2 4b b b2

H B

;

36 bH

2 b2

4b b b2

6 b b

H B

Круг

0,785d2 ;

Ix Iy

0,05d

;

W W

0,1d3

;

уСимметричный двутавр, составленный

из прямоугольников

a х

A ah b(H h);

H h О

(H3 h3);

a3h

(H h).

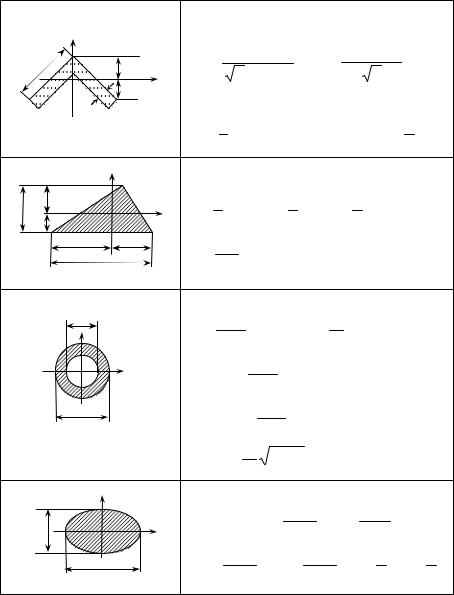
Окончание таблицы 13

Равнобокий уголок

A t(2h t);

ht t2

h t 2c

уB

; yH

;

уH

2(2h t)

c yB cos45o ;

2(c t)

)

t(h 2c

Треугольник

уB

уH

bс

2bh;

yH 3h;

3 h;

bа

; ix

0,2357h.

Кольцо

A D (1 c2) ; c d ;

О х

Ix Iy D4 (1 c4);

W W

D3 (1 c4);

1 c2 .

Эллипс

A ab; Ix ab3

; Iy a3b ;

ab2

2а

; Wy

; ix 2 ; iy 2 .

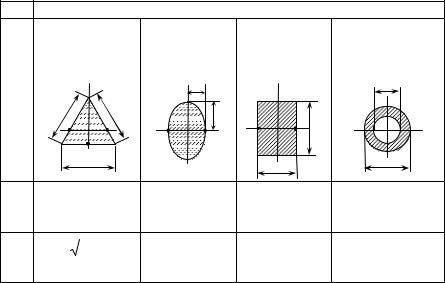
Геометрические характеристики для определения напряжений и углов поворота стержней при кручении

Сечение

Wк

Iк

	Mкр		М	*
max		,		крl
	W		GI		к
	к

	Сечения		Т а б л и ц а 14
В форме рав-
	Эллипти-	Прямо-
носто-роннего			Кольцевое
	ческое	угольное
треугольника

	b		d

а	а			a		А a
А	А	А	А	А		А a
	А					D
	а				b	D
					b

	a	3				ab			2										d			4
												2	a	0,2D			3		d
												2					3						4
20								2				b					1		D				4
20								2											D
								3		2					D	4		d		4
								3		2						4				4
3				4	a b							3
3				4	a b							3
80			a		a		2	b			2	b	a	32			1	D			4
80					a			b						32				D

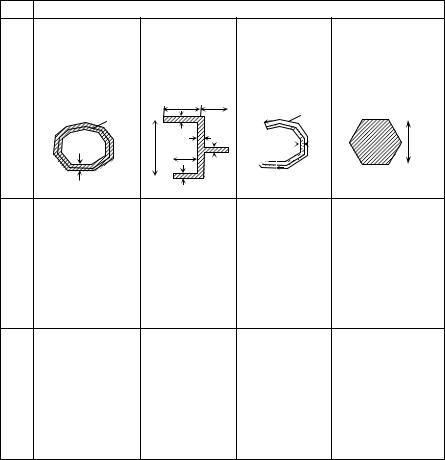
Сечение

Wк

Iк

Окончание таблицы 14

Тонкостенные сечения

Правильный

Замкнутый

Составной

Открытый

шестиили

профиль

восьми-

угольник

δ1

δ2

δ3

2A* min

δ4

k' Ad

Для шести-

A* - площадь

Iк

1 2

угольника

фигуры, огра-

k' 0,217,

min

ниченная

для восьми-

средней лини-

угольника

ей профиля

k' 0,223

kAd2

4A*2

Для шести-

угольника

k 0,133,

i3si

для восьми-

угольника

k 0,130

Значения коэффициента φ в зависимости от гибкости λ

Т а б л и ц а 15

			Значения φ для
	Стали
Гибкость,	марок	Сталь		Высоко
λ	Ст1,	марки		ко-	Чугун	Дерево
λ	Ст2,	марки		прочная	Чугун	Дерево
	Ст3,	Ст5		сталь
	Ст3,			сталь
	Ст4
0	1,00	1,00		1,00	1,00	1,00
10	0,99	0,98		0,97	0,97	0,99
20	0,96	0,95		0,95	0,91	0,97
30	0,94	0,92		0,91	0,81	0,93

40	0,92	0,89		0,87	0,69	0,87
50	0,89	0,86		0,83	0,57	0,80
60	0,86	0,82		0,79	0,44	0,71

70	0,81	0,76		0,72	0,34	0,60
80	0,75	0,70		0,65	0,26	0,48
90	0,69	0,62		0,55	0,20	0,38
100	0,60	0,51		0,43	0,16	0,31
110	0,52	0,43		0,35	-	0,25
120	0,45	0,37		0,30	-	0,22
130	0,40	0,33		0,26	-	0,18
140	0,36	0,29		0,23	-	0,16
150	0,32	0,26		0,21	-	0,14

160	0,29	0,24		0,19	-	0,12
170	0,26	0,21		0,17	-	0,11
180	0,23	0,19		0,15	-	0,10

190	0,21	0,17		0,14	-	0,09
200	0,19	0,16		0,13	-	0,08

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.2015209.41 Кб141Спирт.doc
#
12.03.20151.29 Mб155СпиртыФенолы.doc
#
12.03.201526.62 Кб133список вопросов РМТО.doc
#
12.03.201517.69 Кб118Список использованных источников.docx
#
27.11.20193.47 Mб459Справочник ТСТ.DOC
#
12.03.2015586.7 Кб29Справочные сведения по дисциплине СМ ().pdf
#
12.03.2015574.05 Кб16спрос и предложение.pdf
#
12.07.2019145.41 Кб6Сравнение ИП или ООО.doc
#
12.03.2015236.58 Кб66среда презентация 1.docx
#
30.07.2019129.54 Кб7Средневековье.doc
#
01.04.20252.86 Mб1Средства закрытия КУИ.doc