§2. Методы исследования функций классического анализа

Применение понятия «производной функции» при решении

практических экстремальных задач

При реше­нии многих экстремальных задач часто используют различные частные приемы. Однако суще­ствует достаточно общий прием решения таких задач, основан­ный на методах математического анализа. Интересно напомнить, что одна из причин возникновения математического анализа (особенно дифференциального исчисления) связана с необходи­мостью решения практических экстремальных задач. Из курса «Алгебра и начала анализа» для IX. класса известно, что для нахождения наибольшего и наименьшего зна­чений функции у = f (х), дифференцируемой в ] а;b [, можно поступить следующим образом:

1. Найти все критические точки функции, принадлежащие [а; b],

2. Найти значения функции в этих точках и на концах про­межутка. Наибольшее и наименьшее из этих чисел будут соот­ветственно наибольшим и наименьшим значениями функции на отрезке.

Нетрудно видеть, что если непрерывная функция дифферен­цируема в интервале и имеет единственный экстремум, то в слу­чае максимума это будет ее наибольшее значение, а в случае минимума — наименьшее. При этом правило нахождения наи­большего и наименьшего значений функции упрощается.

Задача 1. Найти наибольшее и наименьшее значения функции f(х) = х³ - 3х² + 1 на [-1; 4].

Решение. Найдем производную функции f(х) : f´(х) = 3х² - 6х Она существует во всех точках.. Решив уравнение Зх² - 6х = 0, найдем критические точки:

х₁ = 0, х₂= 2. Теперь составим та­блицу значений функции в критических точках и на концах отрезка:

Х	-1	0	2	4
f(х)	-3	1	-3	17

Из этой таблицы видно, что наименьшее значение равно —3, а наибольшее 17.

Задача 2. Найти наименьшее и наибольшее значения функции у = х²- 2х + 3 на [0; 2].

Решение. Функция имеет единственный экстремум (минимум) в точке х = 1, которая принадлежит отрезку [0; 2]. Поэтому x = 1 есть наименьшее значение данной функции на [0; 2]. Далее, y(0) = 3, y(2) = 3. Наибольшее значение (3) функция достигает на обоих концах отрезка.

Выпуклость множества допустимых решений

задачи и целевой функции.

Для решения задач математического программирования существенно важно знать:

1) Выпукло или не выпукло множество допустимых решений задачи;

2) Яв­ляется ли целевая функция выпуклой или вогнутой или она не относится ни к тому, ни к другому классу.

Напомним необходимые определения. Говорят, что множество выпукло, если оно вместе с любыми своими точками А и В со­держит и все точки отрезка АВ. На рис.1. представлены примеры выпуклых множеств точек плоскости. Примерами выпуклых множеств в пространстве могут служить сфера, пира­мида, призма и т. д.

Рис. 1.

Область является выпуклой, если отрезок пря­мой, соединяющей любые две точки области, принадлежит этой области. Следовательно, если х_х и х₂ находятся в этой области, то любая точка вида (θ х₂ + (1 — θ) , где 0 < θ < 1, находится в этой же области. На рис.2. - а изображена выпуклая область, а на рис.1. - б — невыпуклая.

Рис. 2.

На рис.3. изображены примеры невыпуклых множеств. В невыпуклом множестве можно указать хотя бы две точки, такие, что не все точки отрезка АВ принадлежат рассматри­ваемому множеству. Как пример невыпуклого множества в про­странстве можно указать тор.

Рис. 3.

Функцию у = f (х) одной переменной будем называть выпуклой, если отрезок, соединяющий две любые точки её графика, при­надлежит графику или расположен выше его (рис.4.). Функция вогнута, если отрезок, соединяющий две любые точки графика, принадлежит ему или расположен ниже его (рис.5.).

Рис.4. Рис.5.

Аналогично можно сформулировать определения понятий вогнутой и выпуклой функций нескольких переменных. Мы го­ворим, что гиперповерхность Z = f (х_1, х₂, ..., х_п) выпуклая, если отрезок, соединяющий две ее любые точки, лежит на поверхности или выше ее. Гиперповерхность Z = f (х_1, х₂, ..., х_п) вогнута, если от­резок, соединяющий две ее любые точ­ки, лежит на поверхности или ниже ее.

Локальный и глобаль­ный минимум функция f(х).

Функция f(х) имеетлокальный минимум в точке х₀,если существует не­которая положительная величина δ, такая, что если |х - х₀| < δ, тоf(х) ≥ f(х₀) т. е. если существует окрестность точких₀, такая, что для всех зна­ченийх в этой окрестностиf(х) больше f(х₀)

Функция f(х) имеет глобаль­ный минимум в точке х*, если для всехх справедливо неравенство f(х) ≥ f (х^*).

На рис.6. дано графическое представление функции f (х), которая имеет локальный минимум в точкех₀ и глобальный минимум в точкех*.

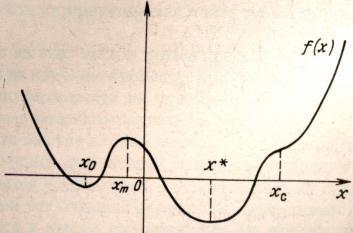
Рис.6.

Классический подход к задаче нахождения значений х₀ их* состоит в поис­ке уравнений, которым они должны удовлетворять. Представленная на рис. функция и ее производные непрерывны, и видно, что в точкахх₀ их* производнаяf''(х), (градиент функции) равна нулю.Следовательно, х₀ и х* будут решениями уравнения f''(х) = 0.Точках_т, в которой достигаетсялокальный максимум, и точках_c, в ко­торой имеется точка горизонтального перегиба функции, также удовлетворя­ют этому уравнению. Следовательно, уравнениеf''(х) = 0 является тольконеобходимым условием минимума, ноне является достаточным условием мини­мума. Заметим, однако, что в точкахх₀ их* производнаяf''(х) меняет знак с отрицательного на положительный. В точкех_т знак

меняется с положитель­ного на отрицательный, в то время как в точке х_с он не меняется. Следова­тельно, производная в минимуме является возрастающей функцией, а по­скольку степень возрастанияf''(х) измеряется второй производной, можно ожидать, что f'''(х₀) > 0,f'''(х^*) > 0, тогда какf'''(х_т) < 0. Если, однако, вторая производная равна нулю, ситуация остается неопре­деленной. Полученные выше результаты могут найти надежное обоснование, если рассмотреть разложение функцииf(х) в ряд Тейлора в окрестности точких₀ (илих*, илих_т), что, конечно, требует непрерывности функцииf (х), и ее производных:

+) + (1.1) Если в точкех₀ достигается минимум, то левая часть (1.1) будет неотри­цательной для любого достаточно малогоh (|h| <δ). Следовательно, первая производнаяf''(х₀) должна быть равна нулю, и это является достаточным условием. Если бы она была положительной, то до­статочно малое отрицательное значение 𝐡делало бы правую часть (1.1) от­рицательной, а если бы она была отрицательной, то достаточно малое поло­жительное значение делало бы правую часть отрицательной. Так как в следующем члене (1.1) всегда ² > 0, то, если f'''(х₀) > 0, в точкех₀ достигается минимум. Если и f'''(х_m) < 0, , то из ана­логичных соображений в точкех_т достигается

максимум. Для определения различия между локальным и глобальным минимумами необходимо срав­нить значения функций f(х₀) и f (х^*).

Пример.

Исследовать характер точек перегиба функции f(х) =х³ - 2х² +х + 1:

Решение. Зх² - 4х+1 = 0, тогда (Зх - 1)(х - 1) = 0, т. е.х = 1/3 илих= 1.

При х = 1/3 производнаяменяет знак с положительного на отрицательный, а при

х = 1 - с отрицательного на положительный. Следовательно, в точкех = 1/3 дости­гается максимум, а в точкех = 1 - минимум. Этот пример может быть решен более простым способом, если вычислить вторую производнуюf''' = 6х — 4: f'''1/3) = -2, т. е. отрицательна, и прих = 1/3 достигается максимум; f'''(1) = 2, т. е. положительна, и прих = 1 достигается минимум. Неоднозначность, возникающую приf'''(*)⁼0, можно разрешить, увели­чив количество членов в формуле разложения в ряд Тейлора

:

+) +

При этом можно сформулировать следующее правило: Если функция f(х) и ее производные непрерывны, то точка х₀является точкой экстремума (максимума или минимума)тогда, и только тогда,когдап четное, гдеn — порядок первой необращающейся в нуль в точкех₀ производной. Если < 0, то в

точке х₀ достигается максимум, если> 0, то в точкех₀ достигается минимум.

Пример 2

Найти точку перегиба функции f (х) = (х - 1)⁶:

Решение. f^' (х) = 6 (х - 1)⁵= 0 при х = 1.

Первой, не обращающейся в нуль в точке х = 1 производной, будетf ⁶(1) = 6. Следова­тельно, функцияf (х) имеет минимум в точкех = 1.

Локальный и глобаль­ный минимум функция Z = f (х_1, х₂, ..., х_п) .

Вспомним еще ряд определений, которые нам потребуются в дальней­шем.

Пусть дана функция Z = f (х_1, х₂, ..., х_п), определенная на замкнутом множестве Ф. Элементами множества Ф являются точки X = (х_1, х₂, .. ., х_п). Поэтому функцию

Z =f (х_1, х₂, ..., х_п) можно записать так: Z =f (х). Говорят, что функция Z =f (х), определенная на некотором замкнутом множестве X, достигает в точке х₀ Х локального максимума (локального ми­нимума), если найдется такое число > 0, что для всех х_, удовлетворяю­щих неравенству |х—х₀| <, выполняется неравенство f(х) ≤ f(х₀) (f(х) ≥ f(х₀) ). Точка х₀, в которой функция дости­гает локального максимума (миниму­ма), называется точкой локального мак­симума (минимума). Рассмотрим при­мер. На рис. 7 изображён график некоторой функции одной переменной, определенной на [1; 10] (заметим, что эта функция не является ни выпук­лой, ни вогнутой). Функция имеет на [1; 10] три точки локального мини­мума (х₁= 3,

х₂ = 6, х₃ = 9) и две точки локального максимума (x₄ = 5, x₅ = 8).

Пусть функция Z = f (х) определена на замкнутом множестве X. Если х₀ Х

и f(х) ≤ f(х₀) (f(х) ≥ f(х₀) ). любой точки х₀ Х, то говорят, что в точке х₀ функция достигает абсолютного максимума (абсолютного минимума). Вместо термина «абсолют­ный» часто используют термин «глобальный». Иными словами, глобальный максимум функции есть ее наибольшее значение в области определения, а глобальный минимум - наименьшее значение. Глобальный максимум и глобальный минимум назы­вают глобальными экстремумами функции. На рисунке 6 пред­ставлен график функции, глобальный минимум которой равен 2

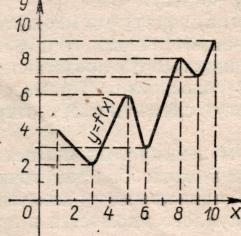
Рис.7

и совпадает с наименьшим из локальных минимумов. Глобальный же максимум, равный 9, достигается функцией в точке x₆ =10 и не совпадает с наибольшим из локальных максимумов.

Экстремумы функций многих переменных

Решение задачи оптимизации существенно усложняется, когда критерий оптимальности является функцией нескольких независи­мых переменных даже при известном аналитическом выражении этой функции. Наибольшие трудности возникают при отсутствии непрерывности у всех или некоторых производных оптимизируе­мой функции. В последнем случае для решения оптимальной за­дачи целесообразно использовать методы нелинейного программи­рования. Ниже рассмотрены необходимые и достаточные условия лишь для непрерывных функций, имеющих к тому же непрерывные про­изводные первого и второго порядков.

Для непрерывной функции многих переменных

R = R (х_{2,………….,}), (111.2)

имеющей непрерывные производные первого и второго порядков по всем переменным (i=1,…, n) , необходимым условием экстремума в точке служит равенство нуля в этой точке первых производных по всем переменным. Другими словами, точки, в которых возможен экстремум функции (111,2), могут быть определены решением системы уравнений:

. i = 1, … , n (111,3)

Для того чтобы проверить, действительно ли точка , координаты которой удовлетворяют системе уравнений (111,3), является точкой экстремума функции (111,2), уже недостаточно проверки экстремальности по всем переменным в от­дельности. В качестве примера рассмотрим задачу отыскания экстремума функции двух переменных:

R= 4-. (111,4)

Система уравнений (111,3) при этом имеет вид:

(a)

Решением ее являются значения:

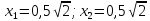(б)

Точка с координатами (б) является точкой, в которой может быть экстремум. Вычисление вторых производных по каждой из переменных в этом случае дает:

. (в)

Из соотношений (в) следует, что по каждой из переменныхи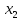в точке (б) функция (111, 4) принимает максимальное значение. Однако можно показать, что точка с координатами (б) в действительности не является точкой экстремума. Наиболее наглядно это доказывается поворотом осей координат на угол 45°. В данном случае для новых координат будут справедливы следующие формулы преобразования :

(г)

Подставляя выражения (г) в соотношение (111,4) с учетом того, что sin45° =cos45°=

найдем

R= 3 + (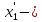l)²- 2()². (111. 5)

Очевидно, что при вращении системы координат экстремальные свойства функции R(, х₂) не нарушаются. Поэтому, вычисляя производные от функ­ции (111,5) по обеим переменным и приравнивая их нулю, получим систему уравнений

2(-1) = 0 ; - 4= 0 , (д)

решение которой определяет положение точки, «подозреваемой» на экстремум в новой системе координат:

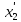=1 ; =0 . (е)

Вычисление вторых производных по каждой из координат в новой системе теперь дает:

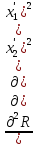. (ж)

Из уравнений (ж) следует, что изучаемая точка не является экстремальной, так как по переменнойфункция (111,5) имеет минимум, а по перемен­ной— максимум. Нетрудно пред­ставить вид поверхности, описывае­мой выражениями (111, 4) или (111,5). Она представляет собой «седло» (рис. 111-8), имеющее точ­ку, в которой первые производные функции по обеим переменным обра­щаются в нуль.Разумеется, что использо­ванная процедура поворота осей координат в общем слу­чае непригодна для практиче­ского исследования точек, по­дозреваемых на экстремум. В особенности это относится к задачам, в которых число не­зависимых переменных велико.

Поэтому необходимо применять более строгие и общие методы.

Предположим, что исследуется на экстремум точка с координатами:

удовлетворяющими системе уравнений (111,3). Разложим функцию

в окрестности точки (111, 6) в ряд Тейлора по степеням прираще­нии переменных

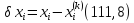
Тогда получим:

В записи выражения (111,9) использована сокращенная форма представления членов разложения с производными выше первого порядка. Например, для функции двух переменных член

раскрывается как

Аналогично раскрываются и члены более высокого порядка при большем числе независимых переменных. Опуская в разложении (111,9) члены, имеющие порядок мало­сти по выше второго, и принимая во внимание, что члены пер­вого порядка малости пообращаются в нуль, поскольку коор­динаты точкиудовлетворяют системе (111,3), получим следую­щее приближенное равенство:

Из выражения (111,11) следует, что знак приращения функции в достаточно малой окрестности точкиопределяется произ­водными второго порядка отR(x) по всем переменным, включая и смешанные производные. Для того чтобы точкаявлялась точ­кой экстремума функцииR(x), достаточно при любых малых приращениях независимых переменныхправой части выражения (111,11) оставаться положительной для точки минимума и отрицательной для максимума. Поскольку вторые производные в выражении (111,11) вычис­ляются в точке, они могут рассматриваться как постоянные числа. В этом случае для анализа знака правой части выражения (111,11) не обязательно требовать малости величин.Taким образом, вопрос о знаке приращения функцииRможет решаться анализом знака квадратичной формы

коэффициенты которой связаны с производными в правой части выражения (111,11) соотношениями

=

Квадратичная форма называется положительно опреде­ленной, если для любых значений z_pона сохраняет положи­тельное значение, за исключением точкиz_p= 0 (р =1, ..., п), в которой она обращается в нуль. Для того чтобы найти, является ли данная квадратичная форма положительно определенной, мож­но воспользоваться теоремой, которая формулируется следующим образом. Для положительной определенности квадратичной фор­мы (111,12) необходимо и достаточно, чтобы были выполнены условия Сильвестра:

(111.14)

Условия (111, 14) означают, что квадратичная форма (111, 12) будет положительно определенной в том случае, если все главные миноры соответствующей ей матрицы

, (111.15)

составленной из коэффициентов, будут строго положительны.

Таким образом, если решен вопрос о положительной опреде­ленности квадратичной формы (111,12), где коэффициенты рас­считываются по формулам (111, 13), то тем самым решается за­дача и о типе точки координаты которой удовлетворяют си­стеме уравнений (111,3), исследуемой на экстремум.Так, когда квадратичная форма, соответствующая правой части выражения (111,11), оказывается положительно определенной, ис­следуемая точка является точкой минимума.Если условия положительной определенности не выполняются, но все главные миноры матрицы (111,15), имеющие нечетный по­рядок, отрицательны, т. е. для миноров нечетного порядка в нера­венствах (111, 14) знак неравенств изменяется на обратный, то квадратичная форма (111,12) будет отрицательно опреде­ленной и, следовательно, функция R(x)в точке имеет максимум.Если же условия положительной и отрицательной определенностей квадратичной формы (111,12) не выполняются, но все главные миноры отличны от нуля, то в исследуемой точке функцияR(x) не имеет ни максимума, ни минимума. При обращении в нуль главных миноров матрицы (111, 15) вопрос о наличии экстре­мума в исследуемой точке решается сложнее, с использованием производных более высокого порядка.

Рассмотрим некоторые частные случаи достаточных условий экстремума, которые могут быть получены из условий Сильвестра (111,14).

Случай двух переменных. Достаточным условием минимума является по­ложительность главных миноров первого и второго порядков, что, принимая во внимание соотношения (111, 13), дает два условия относительно значений вторых производных функции R(x):

*

Достаточным условием максимума в точке 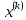является выполнение усло­вия

(111, 17), т. е. положительность четного минора, и одновременное выполнение условия отрицательности первого (нечетного) минора:

Проверим выполнение полученных условий для функции (111,4), для чего необходимо в дополнение к производным (в) вычислить значение смешанной производной, которое при этом будет равно:

Подставляя в соотношение (111, 17), которое должно выполняться для экстремальной точки любого типа, значения производных из выражений (в) и (и), получим, что это условие не выполняется. Следовательно, функция R(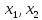), определяемая выражением (111,4), в точке с координатами (б) не; имеет экстремума, что и было получено ранее с использованием вращения] осей координат.

Случай трех переменных.О наличии или отсутствии экстремума в точке, для которой первые производные по всем переменным обращаются в нуль можно в этом случае судить по знакам трех главных миноров:

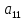=; (111,19)

При получении развернутых выражений главных миноров (111,20) (111,21) использовалось свойство симметрии матрицы (111,15), которое дует из определения ее элементов (111, 13), так как для непрерывных функций имеющих непрерывные производные до второго порядка, справедливо равенство:

Достаточным условием минимума для функции трех переменных является; положительность всех трех миноров (111, 19) —(111, 21), т. е.

Достаточным условием максимума служит положительность четных мино­ров (111,20) и отрицательность нечетных миноров (111,19) и (111,21), т. е.

Аналогичным образом могут быть получены достаточные условия и при большем числе переменных.