Вывод распределения

Рассмотрим состояние частицы в системе, состоящей из множества частиц. Энергия такой частицы равна . Например, если наша система — это некий квантовый газ в «ящике», то подобное состояние может описываться частной волновой функцией. Известно, что для большого канонического ансамбля, функция распределения имеет вид

где

 — энергия состояния ,

 — число частиц, находящихся в состоянии ,

 — химический потенциал,

 — это индекс, пробегающий все возможные микросостояния системы.

В данном контексте, система имеет фиксированные состояния. Итак, если какое либо состояние занято частицами, то энергия системы — . Если состояние свободно, то энергия имеет значение 0. Будем рассматривать равновесные одночастичные состояния как резервуар. После того, как система и резервуар займут одно и то же физическое пространство, начинает происходить обмен частицами между двумя состояниями (фактически, это явление мы и исследуем). Отсюда становится ясно, почему используется описанная выше функция распределения, которая, через химический потенциал, учитывает поток частиц между системой и резервуаром.

Для фермионов, каждое состояние может быть либо занято одной частицей, либо свободно. Поэтому, наша система имеет два множества: занятых (разумеется, одной частицей) и незанятых состояний, обозначающихся и соответственно. Видно, что , , и , . Поэтому функция распределения принимает вид:

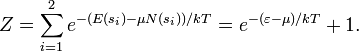
Для большого канонического ансамбля, вероятность того, что система находится в микросостоянии вычисляется по формуле

Наличие состояния, занятого частицей, означает, что система находится в микросостоянии , вероятность которого

 называется распределением Ферми — Дирака. Для фиксированной температуры , есть вероятность того, что состояние с энергией будет занято фермионом. Обратите внимание, что является убывающей функцией от . Это соответствует нашим ожиданиям: высокоэнергетические состояния занимаются с меньшей вероятностью.

Обратите внимание, что энергетический уровень имеет вырождение . Теперь можно произвести простую модификацию:

Это число — ожидаемое число частиц, в суммарном состоянии с энергией .

Для всех температур , . Это означает, что состояния с энергией всегда будут иметь одинаковую вероятность быть заполненными или свободными.

В пределе , становится ступенчатой функцией (см. первый график). Все состояния с энергией меньше химического потенциала будут заняты с вероятностью 1. Состояния с энергией выше химического потенциала будут свободны. Химический потенциал при нулевой температуре — энергия Ферми, обозначается , то есть 

Влияние температуры

Необходимо заметить, что химический потенциал зависит от температуры. Однако для систем, имеющих температуру ниже температуры Ферми , что часто используется, как аппроксимация, . В реальности же:

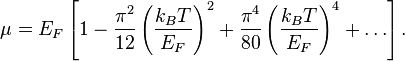
10. Магнитное поле. Вектор магнитной индукции. Закон Био-Савара-Лапласа. Закон Ампера. Сила Лоренца.

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1], магнитная составляющая электромагнитного поля^.

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля^[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 10⁴ Гс