Электрический диполь

Совокупность двух равных по величине разноименных точечных зарядов q, расположенных на некотором расстоянии друг от друга, малом по сравнению с расстоянием до рассматриваемой точки поля называется электрическим диполем.(рис.13.1)

Произведение называется моментом диполя. Прямая линия, соединяющая заряды называется осью диполя. Обычно момент диполя считается направленным по оси диполя в сторону положительного заряда.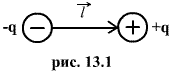

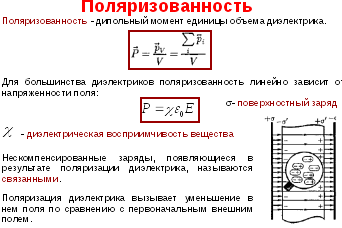
Поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов:

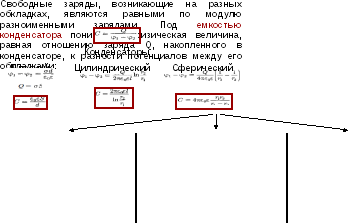
4. Проводники в электростатическом поле. Распределение зарядов на поверхности и в объеме проводника. Электрическая емкость уединенного проводника. Конденсаторы, последовательное и параллельное соединение конденсаторов.

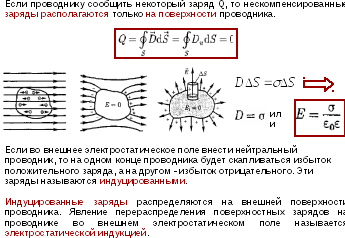
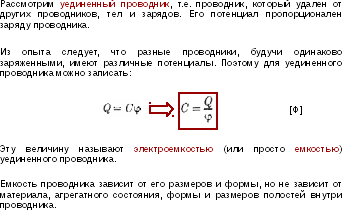
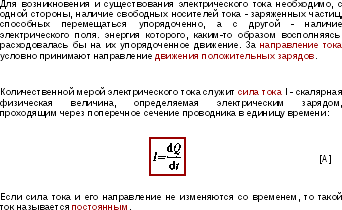
5. Электрический ток. Постоянный и переменный электрический ток. Плотность тока. Электродвижущая сила и напряжение. Сторонние силы.

6. Закон Ома для участка цепи в интегральной и дифференциальной форме. Закон Джоуля-Ленца. Закон Ома для неоднородного участка цепи и замкнутой цепи. Правила Кирхгофа для разветвленных цепей.

Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока.

В словесной формулировке звучит следующим образом

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величинунапряженности электрического поля

Математически может быть выражен в следующей форме:

где  — мощность выделения тепла в единице объёма,  — плотность электрического тока,  — напряжённость электрического поля, σ — проводимость среды.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах^[3]:

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке исопротивления участка

В математической форме этот закон имеет вид

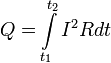
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t₁ доt₂. В случае постоянных силы тока и сопротивления:

7. Распределение Ферми-Дирака. Функция распределения. Зависимость уровня Ферми от температуры.

Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет распределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии; предложена в 1926 году итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком, который выяснил её квантово-механический смысл; позволяет найти вероятность, с которой фермион занимает данный энергетический уровень.

Работы по статистике Ферми — Дирака были опубликованы в 1926 году, а в 1927 она была применена Арнольдом Зоммерфельдом к электронам вметалле.

В статистике Ферми — Дирака среднее число частиц в состоянии с энергией есть

где

 — среднее число частиц в состоянии ,

 — энергия состояния ,

 — кратность вырождения состояния (число состояний с энергией ),

 — химический потенциал (который равен энергии Ферми при абсолютном нуле температуры),

 — постоянная Больцмана,

 — абсолютная температура.

В (идеальном) ферми-газе в пределе низких температур . В этом случае (полагая уровни энергии невырожденными ), функция распределения частиц называется функцией Ферми:

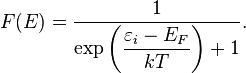
Статистики Ферми — Дирака и Бозе — Эйнштейна применяются в том случае, когда необходимо учитывать квантовые эффекты, когда частицы обладают «неразличимостью». Квантовые эффекты проявляются тогда, когда концентрация частиц (где  — квантовая концентрация).

Квантовая концентрация — это концентрация, при которой расстояние между частицами соразмерно с длиной волны де Бройля, то есть когда волновые функции частиц соприкасаются, но не перекрываются. Квантовая концентрация зависит от температуры. Статистика Ферми — Дирака (Ф — Д) применяется к фермионам (частицы, на которые действует принцип Паули),статистика Бозе — Эйнштейна (Б — Э) применяется к бозонам. Оба этих распределения становятся распределением Максвелла — Больцмана при высоких температурах и низких концентрациях.

Распределением Максвелла — Больцмана часто описываются классические «различимые» частицы. Другими словами, конфигурация частицы в состоянии 1 и частицы в состоянии 2 отличается от конфигурации частицы в состоянии 1 и частицы в состоянии 2. Когда эта идея была проработана полностью, оказалось, что распределение частиц по энергетическим состояниям приводит к нефизическим результатам для энтропии, что известно, как парадокс Гиббса. Эта проблема исчезла, когда стал ясен тот факт, что все частицы неразличимы. И Ф — Д, и Б — Э приближаются к статистике Максвелла — Больцмана в пределе высоких температур и низких плотностей. Статистика Максвелла — Больцмана хорошо описывает поведение газов. Ф — Д часто используется для описания электронов в твердых телах, на ней, к примеру, базируются основные положения теории полупроводников в частности и электроники в целом.