15. Область применимости молекулярной динамики

Метод молекулярной динамики (МД) позволяет моделировать детальную микроскопическую картину внутренней подвижности систем, состоящих из молекул. В его основе лежит расчет классических (ньютоновских) траекторий движения взаимодействующих классических частиц в фазовом пространстве их координат и импульсов.

Методы МД-моделирования являются мощными способами расчета моделей наноразмерных материалов, подходят для исследования статических и динамических свойств наноструктур. По своей природе это методика расчета, подходящая для предсказания поведения наносистем, состоящих из конечного числа частиц. Посредством МД-моделирования можно точно связать коллективную динамику конечного числа частиц с динамикой отдельной частицы, рассмотреть образование молекулы в результате возникновения ко валентных связей. Также можно изучить, как вследствие нековалентных взаимодействий происходит самосборка молекулярных «строительных» блоков для получения материалов с предпочтительными свойствами.

16. Базовые законы молекулярно-динамического моделирования

Атомы и молекулы твердого тела или кластера могут рассматриваться как объекты классической механики. В общем случае, чтобы определить, можно ли трактовать частицу как классический объект, необходимо сравнить размер атома с длиной волны де Бройля.

Волны де Бройля - волны, связанные с любыми микрочастицами и отражающие их волновую природe. Если частица имеет энергию Е и импульс,то с ней связана волна, частота которой. длина, гдеh-постоянная Планка; m - масса; v- скорость, .

МД-моделирование заключается в численном решении уравнений движения Ньютона для атомов, молекул или ансамблей атомов и молекул, составляющих систему, с целью получения зависящих от времени данных о свойствах системы. Уравнения движения - система уравнений, задающая закон эволюции динамической системы во времени. Например, Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и ускорением этой точки:

Третий закон Ньютона - материальные точки взаимодействуют друг сдругом с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Отсюда вытекает закон сохранения механической энергии взаимодействующих тел:

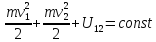
Где -потенциал взаимодействия двух тел, зависящий отмодуля разности координат этих тел.

17. Выбор шага по времени в молекулярной динамике

Важной операцией является выбор шага по времени . Примоделировании микроканонического ансамбля полная энергия системы должна сохраняться. Если величинабудет слишком большой, то шаги тоже станут чрезвычайно большими, и частица может войти в область, запрещенную для классического движения. Это может происходить, например, в том случае, если сталкиваются две частицы. Вхождение в область, запрещенную в классической механике, означает, что значение потенциальной энергии стало больше, чем максимально допустимое. Тогда полная энергия тоже возрастает. Таким образом, в зависимости от соответствующей величины полной энергии приращениеследует выбирать достаточно малым, но при этом и не слишкоммаленьким, чтобы при численном решении не потребовалось чрезвычайнобольшого количества шагов. Оптимальное значениеобычно находитсяметодом проб и ошибок. Одна фемтосекунда (с) - хорошая пробная оценкашага для начала, но оптимальное значение зависит от начальной энергии и типарассматриваемого потенциала.

Существуют четыре основных алгоритма, разработанных для облегчения сходимости при МД-моделировании:

•метод Верле;

•метод с перешагиванием («чехарда»);

•ускоренный метод Верле;

•предикторно-корректорный метод.

Длина траектории в молекулярной динамике равняется шагу интегрирования, умноженному на число сделанных шагов. Выбор длины траектории в значительной степени связан с понятием эргодичности траектории. Эргодичность - свойство динамических систем, состоящее в том, что в процессе эволюции почти каждое состояние с определённой вероятностью проходит вблизи любого другого состояния системы.

За время интегрирования система должна много раз побывать во всех значимых областях конфигурационного пространства. Поэтому минимальную длину траектории можно оценить, исходя из значения времени, необходимого для преодоления каждого из энергетических барьеров:

где - время преодоления барьеров; N - количество торсионных углов в молекуле;U- значение энергетического барьера; - постоянная Больцмана; Т- температура.

Время, необходимое для расчета траектории молекулы, можно значительно сократить, уменьшая число степеней свободы. Существует два способа ограничения движений длин валентных связей и углов:

•валентные связи и углы жестко фиксируются;

•на валентные связи и углы накладываются упругие ограничения с очень большой константой упругости.