
- •1.Перечислите предпосылки появления нанотехнологии
- •3.Инструментарий нанотехнологии
- •4.Основные проблемы нанотехнологии и пути их решения
- •5.Уровни научного познания в применении к нанотехнологиям
- •6. Общие принципы компьютерного моделирования
- •7. Типы моделей «белый ящик», «черный ящик», «серый ящик
- •8. Принципиальные подходы вычислительной нанотехнологии
- •9. Основные принципы моделирования молекулярных систем в молекулярной механике
- •10. Потенциальная энергия молекулы в молекулярной механике
- •11. Энергия слабых связей в молекулярной механике
- •12. Методы поиска равновесных структур в молекулярной механике
- •13. Методы упрощения, применяемые в молекулярной механике
- •14. Достоинства и недостатки методов молекулярной механики
- •15. Область применимости молекулярной динамики
- •16. Базовые законы молекулярно-динамического моделирования
- •17. Выбор шага по времени в молекулярной динамике
- •18. Методы ограничения областей в молекулярной динамике
- •19.Методы учёта энергообмена с внешней средой в молекулярной динамике
- •20. Достоинства и недостатки молекулярной динамики
- •21. Стохастический принцип моделирования в методах Монте-Карло
- •22. Алгоритм Метрополиса
- •23. Процесс Маркова
- •24. Достоинства и недостатки моделирования методами Монте-Карло
- •25. Механизмы образования супрамолекулярных связей
- •26. Водородная связь в супрасистемах
- •27. Электростатические взаимодействия в супрасистемах
- •28. Ван-дер-ваальсовы взаимодействия в супрасистемах
- •29. Достоинства супрамолекулярных систем
- •30. Самоорганизация сложных систем
- •31. Самосборка как пример самоорганизации в нанотехнологии. Факторы, определяющие самосборку
- •32. Общие признаки пакетов моделирования молекулярных систем
- •33. Процедура проведения квантовохимического моделирования
- •34. Проведите общий обзор программного обеспечения моделирования наносистем
9. Основные принципы моделирования молекулярных систем в молекулярной механике
Молекулярная механика расчетный эмпирический метод определения геометрических характеристик и энергии молекул. Основан на предположении о том, что энергия молекулы может быть представлена суммой вкладов, включающих связанные с длинами связей, валентными и торсионными углами.
В настоящее время термин «молекулярная механика» употребляется для определения широко используемого метода, позволяющего провести точный расчет геометрического строения молекул и их энергии на основе имеющихся экспериментальных данных. Он использует классическую идею о химических связях между атомами в молекуле и ван-дер-ваальсовых силах, действующих между валентно-несвязанными атомами.
В молекулярной механике электроны явным образом не рассматриваются, а лишь считаются причиной возникновения того потенциального поля, в котором находятся ядра. А величина этого потенциала определяется эмпирическим путем.
В молекулярной механике в расчетах применяется большое число параметров. Для каждой данной молекулы они должны быть известны из предыдущих исследований других молекул того же класса. Таким образом, область применения молекулярной механики ограничивается в том смысле, что изучаемая молекула должна принадлежать к заранее исследованному классу соединений.
При рассмотрении структур, находящихся на потенциальной поверхности, полезно придерживаться определенной терминологии. Каждой точке, относящейся к минимуму энергии, соответствует конформер. Для перехода изодного минимума в другой молекула должна пройти через разделяющую их седловую точку (перевал). В седловой точке реализуется затененная конформация с несколько растянутыми связями и деформированными валентными углами.
10. Потенциальная энергия молекулы в молекулярной механике
Если молекула, состоящая из N атомов и описываемая 3Nкоординатами xh деформируется по отношению к своей равновесной конфигурации с энергиейU0и координатами х0, то ее потенциальную энергию можно разложить в ряд Тейлора:

Потенциальная
энергия молекулы целиком имеет
электромагнитную природу и обычно
задается в виде суммы отдельных
составляющих:

которые
соответствуют следующим типам
взаимодействий:
 –
потенциальная энергия валентных связей;
–
потенциальная энергия валентных связей; -
валентных углов;
-
валентных углов;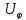 -
торсионных углов;
-
торсионных углов; -плоских
групп;
-плоских
групп; -
ван-дер-ваальсовых сил;
-
ван-дер-ваальсовых сил; -
электростатических сил;
-
электростатических сил; -
водородных связей. Эти составляющие
имеют различный функциональный вид.
-
водородных связей. Эти составляющие
имеют различный функциональный вид.
Валентные
связи
поддерживаются за счет потенциала
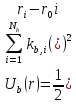 .
гдеi-
номер связи в молекуле;
.
гдеi-
номер связи в молекуле;
 -
полное число валентных связей;
-
полное число валентных связей; -эффективная жесткость валентной связи;
-эффективная жесткость валентной связи; - длина связи:
- длина связи: –
равновесная длина связи. При расчетах
обычно заменяют реальный потенциала,
описывающий валентные взаимодействия,
на параболический.
–
равновесная длина связи. При расчетах
обычно заменяют реальный потенциала,
описывающий валентные взаимодействия,
на параболический.
Валентные
углы
задаются потенциалом
 .
Гдеi
- номер валентного угла;
.
Гдеi
- номер валентного угла;
 -
полное число валентных углов;
-
полное число валентных углов; -эффективная упругость валентного
угла;
-эффективная упругость валентного
угла; - значение валентного угла; -
- значение валентного угла; - его
равновесное значение.
его
равновесное значение.
Энергия
торсионных
взаимодействий
и потенциалов, соответствующих плоским
группам,
записывают в одинаковом виде:

где
 - номер торсионного угла;
- номер торсионного угла; - номер гармоники;
- номер гармоники; - константа:
- константа: -вклад
гармоники в потенциал торсионного
угла;
-вклад
гармоники в потенциал торсионного
угла; —
кратность гармоники.
—
кратность гармоники.
Потенциалы
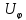 и
и отличаются
константами.
отличаются
константами.
Ван-дер-ваальсовы
взаимодействия атомов, разделенных
тремя и более валентными связями,
описываются потенциалами Леннард-Джонса:
 .
Параметры потенциала А и В зависят от
типов атомовi
и j,
участвующих во взаимодействии;
.
Параметры потенциала А и В зависят от
типов атомовi
и j,
участвующих во взаимодействии;
 ,-
где
,-
где ,
и
,
и - координаты взаимодействующих атомов.
- координаты взаимодействующих атомов.
Электростатические
взаимодействия задают кулоновским
потенциалом;
 ,
где
,
где -
парциальные заряды на атомах:
-
парциальные заряды на атомах: - диэлектрическая проницаемость среды.
- диэлектрическая проницаемость среды.
Водородные
связи
возникают и исчезают в процессе движения
атомов между теми из них, которые имеют
электростатические взаимодействия.
Функциональный вид потенциала водородной
связи похож на потенциал ван-дер-ваальсовых
взаимодействий, но с более короткодействующими
силами притяжения: .
.
