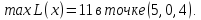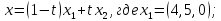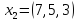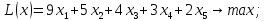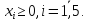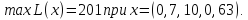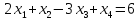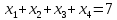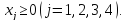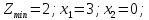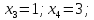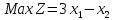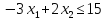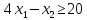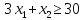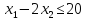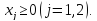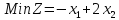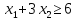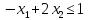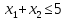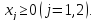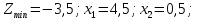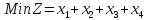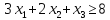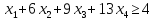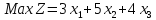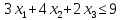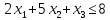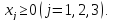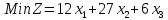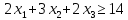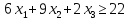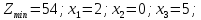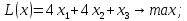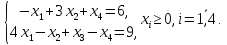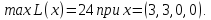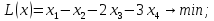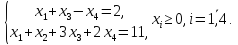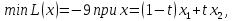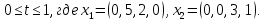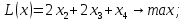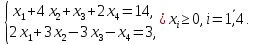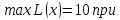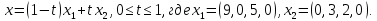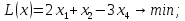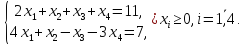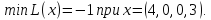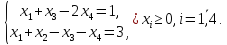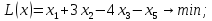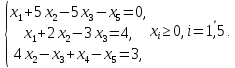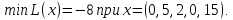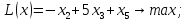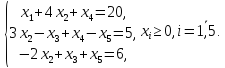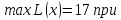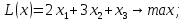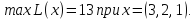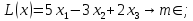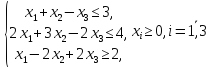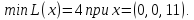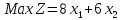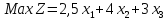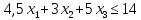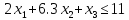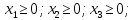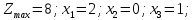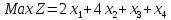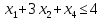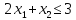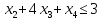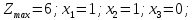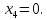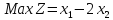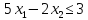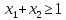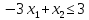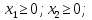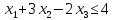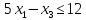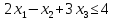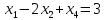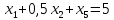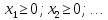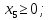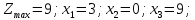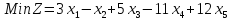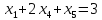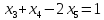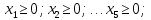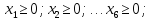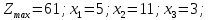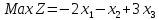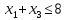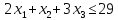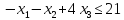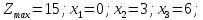- •§1. Этапы решения задачи
- •§2. Некоторые сведения из линейной алгебры.
- •§ 3. Классификация методов математического программирования.
- •§4. Методы исследования функций классического анализа (Аналитические методы)
- •4.1. Необходимые и достаточные условия безусловного экстремума функции
- •4.2. Необходимые и достаточные условия условного экстремума. Принцип Лагранжа.
- •§5. Методы исследования функций численного анализа.
- •Раздел 1.
- •Глава 1. Метод линейного программирования
- •§1. Примеры составления задач лп
- •§ 2. Геометрическая интерпретация решения задачи лп.
- •§ 3. Алгоритм решения канонической задачи лп симплексным методом (метод Данцига).
- •1) Найдется хотя бы одна положительная (отрицательная) оценка и в каждом столбце с такой оценкой найдется хотя бы один положительный элемент, то можно улучшить решение, выполнив следующую итерацию;
- •2) Найдется хотя бы одна положительная (отрицательная) оценка, столбец которой не содержит ни одного положительного элемента, то функция не ограничена в области допустимых решений;
- •§ 4. Решение почти канонических задач.
- •§ 5. Вырожденная задача лп.
- •Глава 2. Решение основной задачи линейного программирования.
- •§1 Сведение основной задачи к двум каноническим.
- •Метод искусственного базиса
- •2. Если линейная система уравнений обладает планами, то существует равносильная ей каноническая система, которую можно получить из завершающей симплексной таблицы вспомогательной задачи [4].
- •3. Далее решаем каноническую (или почти каноническую) задачу лп: минимизировать (максимизировать) целевую функцию f основной задачи лп при условиях (***).
- •§2. Задача о диете
- •Глава 3. Целочисленное линейное программирование.
- •§1 Метод Гомори
- •§2.Пример постановки задачи рационального раскроя [4, c.176].
- •Глава 4. Теория двойственности в лп
- •§ 1. Симметричные двойственные задачи
- •I и II задачи имеют решение.
- •§2. Несимметричные двойственные задачи.
- •Раздел 2. Нелинейное программирование
- •Глава 1.
- •§ 1. Задачи нелинейного программирования с линейной целевой функцией и нелинейной системой ограничений.
- •§ 2. Задачи нелинейного программирования с линейной системой ограничений, но нелинейной целевой функцией.
- •§ 3. Задачи нелинейного программирования с нелинейной системой ограничений и нелинейной целевой функцией.
- •§4. Градиентный метод нелинейного программирования.
- •§5. Выпуклое программирование.
- •Геометрическая интерпретация и графический способ решения задачи квадратичного программирования
- •§6. Параметрическое программирование.
- •Глава 2. Динамическое программирование.
- •Глава 3. Метод случайных испытаний.
- •Глава 4. Геометрическое программирование.
I и II задачи имеют решение.
Одна имеет (
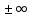 ),
значит другая решения не имеет.
),
значит другая решения не имеет.Обе задачи решения не имеют.
Решение IIзадачи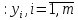 – оптимальные оценки.
– оптимальные оценки.
Эти оценки были введены Л. В. Конторовичем как «разрешающие множители» или по-другому, «объективно-обусловленные оценки».
§2. Несимметричные двойственные задачи.
Рассмотрение
таких задач часто полезно в ЛП. Причём
эти задачи сводятся к симметричным.
Задача I
– основная задача ЛП, задача II
задача минимизации, но
 воII задаче
могут быть любого знака.
воII задаче
могут быть любого знака.
Сведение
осуществляется следующим образом. Как
известно, равенство
 равносильно паре неравенств
равносильно паре неравенств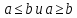 ;
или
;
или .
В задачеIкаждое уравнение
заменяется парой неравенств такого
рода. Тогда задачаIбудет
задачей максимизации с «n»
переменными и «2m»
неравенствами. Затем выписываем
симметричную ей двойственную задачу.
Например, дано:
.
В задачеIкаждое уравнение
заменяется парой неравенств такого
рода. Тогда задачаIбудет
задачей максимизации с «n»
переменными и «2m»
неравенствами. Затем выписываем
симметричную ей двойственную задачу.
Например, дано:
|
Задача I |
Задача II |
|
при условиях:
Ответ: (2,3,0,0)
|
при условиях:
Ответ:
(-1,-2),
|
Сведем к паре симметричных двойственных задач ЛП
|
Задача I |
Задача II |
|
при условиях:
|
при условиях:
|
У задачи II,
когда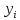 – любого знака, любой план называется
псевдопланом.
– любого знака, любой план называется
псевдопланом.
Теорема:Если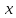 *
некоторый план задачиI,
а
*
некоторый план задачиI,
а *
- некоторый псевдоплан задачиIIиf(x*)=g(y*),
тоx*иy*оптимальные план и псевдопланIиIIзадачи.
*
- некоторый псевдоплан задачиIIиf(x*)=g(y*),
тоx*иy*оптимальные план и псевдопланIиIIзадачи.
|
Глава 5. Примеры задач оптимизации . | |||
|
§1. Решить задачи оптимиэации графическим методом (1-7). | |||
|
№ |
задача |
ответ | |
|
1 |
|
| |
|
2 |
|
| |
|
3 |
|
| |
|
4 |
|
| |
|
5 |
|
.
| |
|
6 |
|
Система ограничений несовместна. | |
|
7 |
|
| |
|
§2. Решить задачи оптимизации симплексным методом (8 – 34). | |||
|
8 |
|
| |
|
9 |
|
| |
|
10 |
|
| |
|
11 |
|
| |
|
12 |
|
| |
|
13 |
|
| |
|
14 |
|
| |
|
15 |
|
| |
|
16 |
|
| |
|
17 |
|
| |
|
18 |
|
Линейная форма не ограничена.
| |
|
19 |
|
| |
|
20 |
|
| |
|
21 |
|
| |
|
22 |
|
| |
|
23 |
|
| |
|
24 |
|
| |
|
25 |
|
| |
|
26 |
|
| |
|
27 |
|
| |
|
28 |
|
Нет решений.
| |
|
29 |
|
| |
|
30 |
|
| |
|
31 |
|
| |
|
32 |
|
| |
|
33 |
|
| |
|
34 |
|
| |
|
§3. Используя метод искусственного базиса для нахождения исходного опорного плана, решить следующие задачи (35 – 52).
| |||
|
35 |
|
| |
|
36 |
|
Линейная форма не ограничена.
| |
|
37 |
|
| |
|
38 |
|
| |
|
39 |
|
| |
|
40 |
|
| |
|
41 |
|
| |
|
42 |
|
| |
|
43 |
|
| |
|
44 |
|
| |
|
45 |
|
| |
|
46 |
|
| |
|
47 |
|
| |
|
48 |
|
| |
|
49 |
|
| |
|
50 |
|
| |
|
51 |
|
Система ограничений несовместна.
| |
|
52 |
|
| |
|
§4. Найти целочисленное решение задач оптимизации (53 – 62).
| |||
|
53 |
|
| |
|
54 |
|
| |
|
55 |
|
| |
|
56 |
|
| |
|
57 |
|
| |
|
58 |
|
| |
|
59 |
|
| |
|
60 |
|
| |
|
61 |
|
| |
|
62 |
|
| |

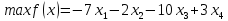
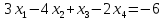
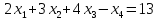

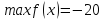

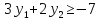
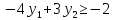


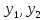 –любого
знака
–любого
знака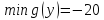
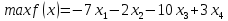
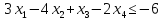

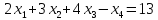

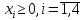

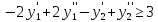
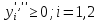
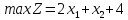

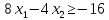
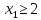
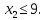
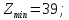
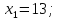

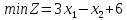
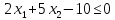

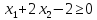
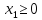
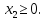




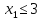
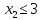
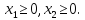

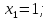

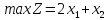
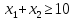
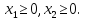
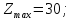
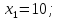
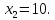
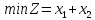

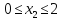
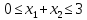
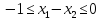
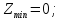
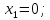
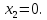

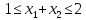
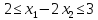

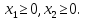
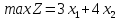
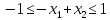


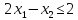
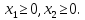


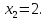
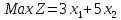
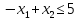
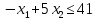
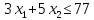
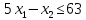

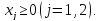

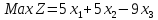
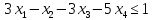
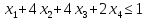
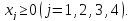
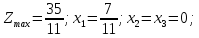

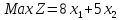

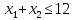
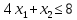
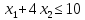
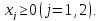


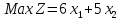
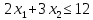
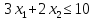

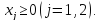

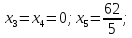



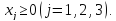




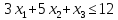

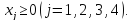
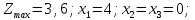
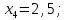

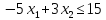

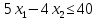
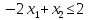
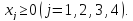
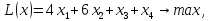
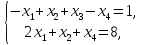
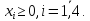
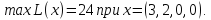
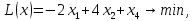

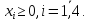

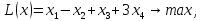
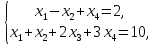
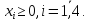
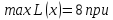
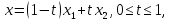

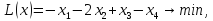
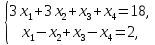
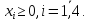
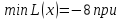
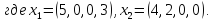
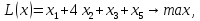

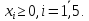


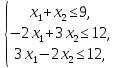


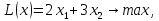








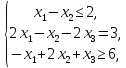
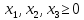 .
.