12. Одноёмкостный объект с самовыравниванием. Статическая и динамическая характеристики. Методика их получения.
Статическая характеристика объекта с самовыравниванием - это эависимость Хвых = f (Хвх) в установившемся режиме
Когда приток увеличивается скачком, например, до 30 л/мин, уровень начинает расти. С ростом уровня возрастает гидростатическое давление на дно сосуда. В результате, увеличивается скорость истечения жидкости из ёмкости – V.
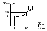
Рис. 2.3. Статическая характеристика объекта c самовыравниванием.
Статическая характеристика строится для определения коэффициента усиления К. Если статическая характеристика нелинейная, как здесь, то её иногда линеаризуют. Если статическая характеристика линейная, то коэффициент усиления для нее только один – общий.
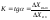
Так как в данном случае характеристика нелинейная, то понятие коэффициента усиления можно отнести только к какой-то точке кривой. Выбирается точка, проводим в ней касательную.
Динамическая характеристика одноёмкостного объекта с самовыравниванием - это эависимость Хвых = f (Хвх) в неустановившемся режиме. Здесь t – время (рис.2.4).
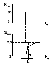
Рис.2.4. Динамическая характеристика объекта c самовыравниванием.
К полученной кривой проводим касательную в точке Хвых = 1 м до пересечения с новым установившимся уровнем Хвых = 2,5м, затем опускаем перпендикуляр. Полученный отрезок на оси времени То – постоянная времени объекта. Ради определения То и была построена динамическая характеристика объекта.
13. Одноёмкостный объект без самовыравнивания. Динамическая характеристика. Методика их получения.
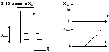
Рис.2.6. Динамическая характеристика объекта без самовыравнивания.
Одноёмкостный объект без самовыравнивания эквивалентен интегрирующему звену (рис.2.6.). При увеличении притока на входе скачком, например, до 30 л/мин, уровень неограниченно растёт, самовыравнивания не наступает, т.к. выходное отверстие ёмкости засорилось (либо там установлен насос постоянной производительности).
14. Многоёмкостный объект с самовыравниванием. Статическая и динамическая характеристики. Методика их получения.
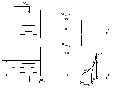
Рис. 2.7. Динамическая характеристика многоёмкостного
объекта с самовыравниванием.
Многоёмкостный объект с самовыравниванием по типу динамической характеристики эквивалентен апериодическому звену II порядка и описывается обыкновенным дифференциальным уравнением II – го порядка с постоянными коэффициентами (две экспоненты). Рассмотрим на примере 2-х ёмкостного объекта.
Динамическая характеристика (рис.2.7.). Эта характеристика описывается дифференциальным уравнением II порядка. Входная величина Xвх, выходная величина Xвых, т.е. уровень во 2-й ёмкости.
После нанесения скачка Xвх с 3 л/мин до 30 л/мин уровень во 2-й ёмкости увеличивается вначале с возрастающей скоростью (здесь f" > 0), а затем с убывающей скоростью (f" < 0). Точка А – это точка перегиба (f" = 0). В итоге, после нанесения скачка Xвх с 3 л/мин до 30 л/мин уровень во 2-й ёмкости установиться на отметке, например, 2,5 м. Здесь Тзап – время запаздывания; То – постоянная времени. Чем больше расстояние между ёмкостями, тем выше смещается точка перегиба А (т.е. увеличивается время запаздывания).