1 Рис.1.12. К определе­нию работы переме­щения заряда в элек­троста­тическом поле. .10. Работа сил электростатического поля при перемещении заряда.

При перемещении заряда в электростатическом поле, действующие на заряд кулоновские силы, совершают работу. Пусть заряд q₀0 перемещается в поле заряда q0 из точки С в точку В вдоль произвольной траектории (рис.1.12). На q₀ действует кулоновская сила

. При элементарном перемещении заряда dl, эта сила совер­шает работу dA

, где  - угол между векторами и. Величинаdlcos=dr является про­екцией вектора на направление силы. Таким образом,dA=Fdr, . Полная работа по перемещению заряда из точки С в В определяется интегра­лом 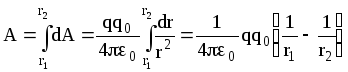, гдеr₁ и r₂ - расстояния заряда q до точек С и В. Из полученной формулы следует, что работа, совершаемая при перемещении электрического заряда q₀ в поле точеч­ного заряда q, не зависит от формы траектории перемещения, а зависит только от начальной и конечной точки перемещения.

В разделе динамики показано, что поле, удовлетворяющее этому условию, яв­ляется потенциальным. Следовательно, электростатическое поле точечного заряда - потенциальное, а действующие в нем силы - консервативные.

Если заряды q и q₀ одного знака, то работа сил отталкивания будет положи­тельной при их удалении и отрицательной при их сближении (в последнем случае ра­боту совершают внешние силы). Если заряды q и q₀ разноименные, то работа сил притяжения будет положительной при их сближении и отрицательной при удалении друг от друга (последнем случае работу также совершают внешние силы).

Пусть электростатическое поле, в котором перемещается заряд q₀, создано сис­темой зарядов q₁, q₂,...,q_n. Следовательно, на q₀ действуют независимые силы , равнодействующая которых равна их векторной сумме. Работа А рав­но­действующей силы равна алгебраической сумме работ составляющих сил, , гдеr_i1 и r_i2 - начальное и конечное расстояния между зарядами q_i и q₀ .

1.11. Циркуляция вектора напряженности электростатического поля.

При перемещении заряда по произвольному замкнутому пути L работа сил электростатического поля равна нулю. Поскольку, конечное положение заряда равно начальному r₁=r₂, то и(кружок у знака интеграла указывает на то, что интегрирование производится по замкнутому пути). Так каки, то. Отсюда получаем. Сократив обе части равенства наq₀, получим или, гдеE_l=Ecos - проекция вектора Е на направление элементарного перемещения . Интегралназываетсяциркуляцией вектора напряженности. Таким обра­зом, циркуляция вектора напряженности электростатического поля вдоль лю­бого замкнутого контура равна нулю. Это заключение есть условие потенциаль­ности поля.

1.12. Потенциальная энергия и потенциал электростатического поля.

Из раздела динамики известно, что любое тело (точка), находясь в потенци­аль­ном поле, обладает запасом потенциальной энергии W_п, за счет которой силами поля совершается работа. Работа консервативных сил сопровождается убылью по­тенци­альной энергии A=W_п1-W_п2 . Используя формулу работы силы электростатического поля по перемещению заря­да, получим

. Отсюда следует, что потенциальная энергия точечного заряда q₀ в поле заряда q равна

, где С - произвольная постоянная. Принято считать, что при r потенциальная энергия обращается в ноль и тогда С=0, а . Из формулы следует, что потенциальная энергия взаимодействия одноимен­ных зарядов положительная и разноименных - отрицательная.

Если поле создано системой зарядов q₁, q₂, ..., q_n, то потенциальная энергия за­ряда q₀ равна . Из полученных выражений видно, что потенциальная энергия зарядаq₀ зависит от его величины и поэтому не может служить энергетической характеристикой дан­ной точки поля.

Отношение потенциальной энергии заряда q₀ к его величине является посто­ян­ным для данной точки поля и уже не зависит от величины q₀. Поэтому мо­жет служить характеристикой поля и называется потенциалом электростатичес­кого поля . Потенциал поля  - скалярная физическая величина, энергетическая характеристика поля, опре­деляемая потенциальной энергией единичного положительного заряда, поме­щенного в эту точку.

Для одиночного заряда q получаем выражение для потенциала поля на расстоянии r от него .

Ранее было записано. Так каки, тои

. Отсюда можно видеть связь между работой в электрическом поле и потенциалами поля. Разность потенциалов двух точек поля определяется работой сил поля при перемещении единичного положительного заряда из точки 1 в точку 2.

Если заряд q₀ перемещать из какой-либо точки поля за его пределы, то r₂, W_п.2=0 и ₂=0. Тогда работа по перемещению зарядаq₀ в бесконечность равна ,.

Отсюда следует, что потенциал точки поля численно равен работе, совершае­мой электрическими силами при перемещении единичного положительного за­ряда из данной точки поля в бесконечность.

Потенциал точки поля системы зарядов q₁,q₂,...,q_n равен алгебраической сумме потенциалов полей всех этих зарядов:

. Единицей потенциала является Вольт (1В=1Дж/1Кл).