Тема 4. Химическое равновесие. Влияние внешних условий на равновесное состояние

Задача №15

Запишите выражения для констант равновесия K_C, K_р и K_N и установите связь между ними для реакции, приведенной в табл. 2.

Решение:

Решение задачи рассмотрим на примере реакции , считая реагирующие вещества идеальными газами.

В условиях равновесия при р, T = const схематическая запись химической реакции имеет вид:

,

где a, b, c, d – стехиометрические коэффициенты веществ A, B, C, D. Для рассматриваемой реакции закон действующих масс устанавливает постоянство отношения произведения равновесных концентраций продуктов реакции к произведению равновесных концентраций исходных веществ, взятых в степенях, равных стехиометрическим коэффициентам, то есть

.

На основании закона действующих масс запишем выражение для константы равновесия K_C для реакции синтеза аммиака.

.

Аналогичным образом записываются формулы для констант равновесия, выраженных через равновесные парциальные давления:

и равновесные мольные доли:

.

Связь между K_р и K_C устанавливается на основании уравнения (9). Для i-го компонента газовой смеси , отсюда:. На основании данного выражения

.

Для реакции синтеза аммиака n = (2) – (1 + 3) = – 2. Следовательно,

.

Связь между K_р и K_N устанавливается на основании закона Дальтона: , гдер – общее давление в системе. Оперируя данным выражением, получим

.

Необходимо отметить, что при расчете констант всегда используется безразмерное относительное давление, равное отношению давления к стандартному значению р^о = 1 атм = 1,01325∙10⁵ Па.

Задача №16

Для реакции, приведенной в табл. 2, рассчитайте константы равновесия K_р, K_C и K_N при 298 К и общем давлении р Па (табл.15). Выразите константу равновесия K_р через состав равновесной смеси, если для проведения реакции исходные вещества взяты в стехиометрическом соотношении.

Таблица 15

Вариант	р·10–6, Па	Вариант	р·10–6, Па
1	9,73	16	9,76
2	9,74	17	9,78
3	9,75	18	9,79
4	9,73	19	9,73
5	9,73	20	9,73
6	9,73	21	9,79
7	9,74	22	9,74
8	9,77	23	9,75
9	9,78	24	9,73
10	9,73	25	9,71
11	9,77	26	9,77
12	9,77	27	9,75
13	9,78	28	9,78
14	9,79	29	9,77
15	9,76	30	9,76

Решение:

Решение задачи рассмотрим на примере реакции . Рассчитаем константы равновесияK_N, K_C и K_р при Т = 298 К и общем давлении 9,73·10⁶ Па, если для проведения реакции исходные вещества взяты в стехиометрическом соотношении (1 моль N₂ и 3 моль H₂).

Значение константы равновесия при температуре 298 К найдем из соотношения

.

Отсюда

.

= –32953,5 Дж (см. задачу №13).

.

Соотношения между K_C, K_р и K_N выведены в задаче 15:

,

где р – относительное давление, т.е. давление, отнесенное к стандартному: р = 9,73·10⁶ / 1,01325∙10⁵ = 96.

,

.

Для расчета состава равновесной смеси определим количество молей в состоянии равновесия.

Обозначим через х число молей NH₃ в момент равновесия. На основании стехиометрии реакции, если образовалось две молекулы NH₃, то израсходована одна молекула азота и три молекулы водорода. Таким образом, если образовалось х молей NH₃, то израсходовано молейN₂ и молейH₂. По условию задачи для проведения реакции взяты 1 моль N₂ и 3 моль H₂. Следовательно, к моменту равновесия в реакционной смеси осталось молейN₂ и молейH₂ .

Рассчитаем общее число молей компонентов реакции в момент равновесия

.

Определим мольную долю каждого компонента реакции при равновесии по формуле (41). Определим также равновесное парциальное давление компонентов на основании закона Дальтона (табл.16).

Таблица 16

Вещество		N2	H2	NH3
Число молей	В начале реакции	y	3y	–
	В момент равновесия
Мольная доля компонента
Равновесное парциальное давление

Выражение для константы равновесия имеет вид:

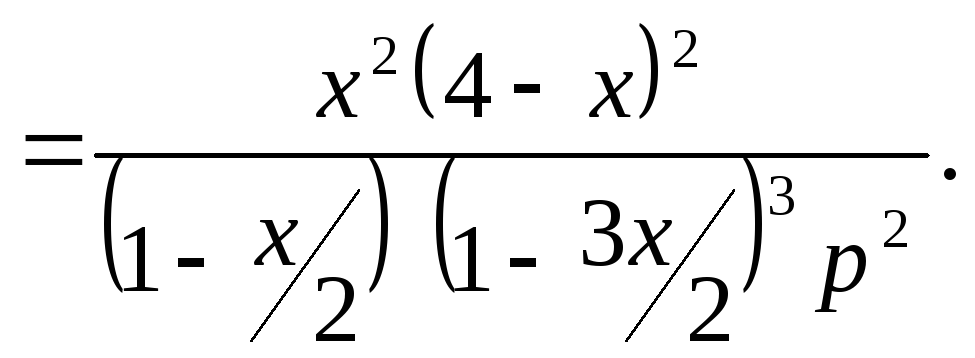
Задача №17

Рассчитайте при температуре Т К (табл. 6) изменение энергии Гиббса G⁰ для реакции, приведенной в табл. 2.

Решение:

Вычислим G⁰ при 800 К для реакции .

Вариант а) Приближенный расчет, в котором принимается энтропия реакции постоянной и не учитывается изменение теплоемкости реакции от температуры (т.е. ). Такое приближенное решение необходимо для быстрой оценки возможности реакции при интересующей нас температуре.

= – ΔS⁰₂₉₈,

Расчет ΔS⁰_{298, реакции} показан в задаче №10. ΔS⁰_{298, реакции} = – 197,74 Дж/К.

Разделим переменные и проинтегрируем:

dG⁰ = ΔS⁰₂₉₈ dT,

,

G_T⁰ = ΔG⁰₂₉₈ – ΔS⁰₂₉₈ (T – 298). (57)

Величину изменении энергии Гиббса для данной реакции при Т = 298 К ΔG⁰_{298, реакции} рассчитываем по справочным данным (см. задачу №13): ΔG⁰_{298, реакции} = – 32960 Дж.

= – 32960 – (–197,74)·(800 – 298) = 66305,5 Дж.

Вариант б) Точный расчет производим по формуле

= – 800·, (58)

последовательно рассчитав точные значения изменения энтропии и теплового эффекта реакции, с учетом зависимости теплоемкостей участников реакции от температуры (т.е. ) (см. задачи №8 и №10):

= – 107815 Дж

= – 230,36 Дж/K.

= – 107815 – 800·(–230,36) = 76473 Дж.

Вариант в) Точный расчет по методу Шварцмана–Темкина с учетом зависимости изменения теплоемкости реакции от температуры производят по уравнению:

. ( 59).

Вычисления по данному уравнению исключают интегрирование и сводятся к умножению и сложению.

В данном уравнении – стандартный тепловой эффект реакции при температуре 298 К,= – 91880 Дж (см. задачу №2);– изменение энтропии в ходе реакции при температуре 298 К,= – 197,74 Дж/К (см. задачу № 10);,и др. –коэффициенты уравнения. Их значения рассчитаны в задаче №7:

–50,12;

36,91·10^–3;

–3,34·10⁵;

–1,15·10^–6.

Коэффициенты при необходимой температуре Т определяем по справочнику. Для температуры 800 К:

,

,

,

.

Во всех трех вариантах расчета значение оказалось положительным в отличие от , т.е. повышение температуры неблагоприятно для протекания реакции в прямом направлении, при температуре Т = 800 К самопроизвольный процесс идет от продуктов реакции к исходным веществам.

Задача №18

Рассчитайте константу равновесия для реакции, приведенной в табл. 2, при 298 К и температуреТ К (табл. 6).

Решение:

Решение задачи рассмотрим на примере реакции образования аммиака . Найдем константу равновесия при температурах 298 К и 800 К.

Значение константы равновесия при температуре 298 К найдем из соотношения

. (60)

Отсюда

.

= –32953,5 Дж (см. задачу №13).

.

Расчет константы равновесия при температуре, отличной от стандартной, можно произвести с различной степенью точности.

Вариант а) Приближенный расчет. Значение константы равновесия при температуре Т можно найти, воспользовавшись уравнением изобары Вант-Гоффа:

( 61)

Считая тепловой эффект реакции постоянным в интервале температур от Т₁ до Т₂. == – 91880 Дж (см. задачу №2).

. ( 62)

После интегрирования уравнения (62) получаем следующее выражение:

,

,

Если Т₁ = 298, то .

,

.

.

Вариант б) Более точный расчет должен учитывать зависимость теплового эффекта реакции от температуры. Эту зависимость можно вывести также с разной степенью точности.

При условии, что теплоемкость не зависит от температуры ()Дж/К (см. задачу №8) получаем уравнение:

.

Подставим полученную зависимость в уравнение изобары Вант–Гоффа:

,

,

,

;

.

Вариант в) Точный расчет. Расчет будет точным, если при выводе уравнения зависимости теплового эффекта реакции от температуры учитывать зависимости теплоемкостей участвующих в реакции веществ от температуры, т.е. учитывать уравнение :

.

По данным задачи №8 уравнение для реакции образования аммиака имеет вид:

= –50,12 + 36,91·10^–3Т – 3,34·10⁵/Т² + 1,50·10^--6Т².

Зависимость теплового эффекта этой реакции от температуры:

После подстановки этой зависимости в уравнение изобары Вант–Гоффа, получим

,

.

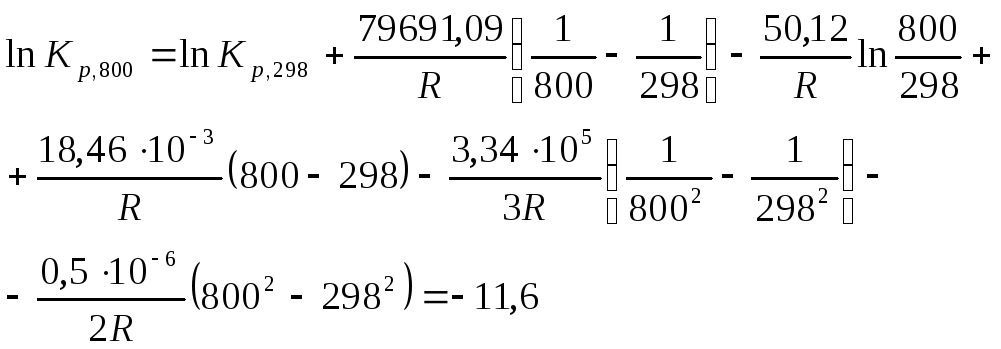
Вариант г) Точный расчет. Константа равновесия реакции образования аммиака при температуре 800 К может быть точно рассчитана по значению изменения энергии Гиббса, которое вычислено с учетом влияния температуры на,иреакции (см. задачу №17): = 76746,6 Дж.

.

Задача №19

Определить направление реакции, приведенной в табл. 2, при температуре Т К (табл. 6) и общем давлении р Па, если число молей неравновесной смеси ,(исходные вещества),,(продукты реакции) даны в табл. 17. Значение константы равновесия при температуреТ взять из задачи №17.

Таблица 17

Вариант					р·10–6, Па
1	0,5	0,2	0,3	–	9,73
2	0,5	0,1	0,5	0,1	9,74
3	0,5	–	0,5	–	9,75
4	0,25	0,25	0,25	0,25	9,73
5	0,3	0,2	0,2	0,3	9,73
6	0,25	0,35	0,15	0,25	9,73
7	0,6	–	0,2	0,2	9,74
8	0,25	0,4	0,25	0,1	9,77
9	0,35	0,3	0,25	0,1	9,78
10	0,1	0,6	0,15	0,15	9,73
11	0,325	–	0,325	0,35	9,77
12	0,4	–	0,3	0,3	9,77
13	0,3	0,3	0,4	–	9,78
14	015	0,15	0,7	–	9,79
15	0,15	0,15	0,35	0,35	9,76
16	0,25	0,25	0,25	0,25	9,76
17	0,5	–	0,15	0,35	9,78
18	0,35	0,5	0,15	–	9,79
19	0,5	0,4	0,1	–	9,73
20	0,3	0,2	0,2	0,3	9,73
21	0,2	0,2	0,6	–	9,79
22	0,55	–	0,15	0,3	9,74
23	0,35	0,55	0,1	–	9,75
24	0,4	–	0,4	0,2	9,73
25	0,25	0,4	0,25	0,1	9,71
26	0,8	0,15	0,15	-	9,77
27	0,3	–	0,3	0,4	9,75
28	0,1	0,6	0,15	0,15	9,78
29	0,25	–	0,25	0,5	9,77
30	0,15	0,15	0,35	0,35	9,76

Решение:

Решение задачи рассмотрим на примере реакции образования аммиака .Определим направление данной реакции при температуре Т = 800 К и общем давлении р = 9,73·10⁶ Па, если число молей компонентов реакции в исходной неравновесной смеси составило = 0,5; = 0,3;= 0,2. Значение константы равновесия(см. задачу № 17).

Установим знак величины .Воспользуемся уравнением изотермы Вант–Гоффа:

, (63),

где – величина, рассчитываемая по той же формуле, что и, но для неравновесных условий, как отношение неравновесных парциальных давлений компонентов реакции ()

.

.

При анализе уравнения изотермы Вант–Гоффа следует рассмотреть три случая:

1) Если > , то > 0, т.е. реакция идет в обратном направлении в сторону образования исходных веществ.

2) Если < , то < 0, т.е. реакция идет самопроизвольно в прямом направлении в сторону образования продуктов реакции.

3) Если = , то = 0, т.е. система находится в равновесии.

Рассчитаем величину через– константу, выраженную через мольные доли компонентов в неравновесной исходной смеси.

.

Для этого рассчитаем величины мольных долей компонентов неравновесной смеси с использованием формулы .

Общее число молей неравновесной смеси

.

Мольные доли компонентов в данном случае:

; ;

численно равны числу молей этих компонентов в системе.

.

Так как < , то выполняется условие (2), следовательно, реакция будет протекать самопроизвольно в прямом направлении. Подтвердим полученные данные расчетом :

Дж/моль.

Задача №20

Оцените влияние температуры и давления на константу равновесия реакции, приведенной в табл. 2. Тепловой эффект реакции взять из решения задачи №2.

Решение:

Решение задачи рассмотрим на примере реакции синтеза аммиака .

а) Для оценки влияния температуры воспользуемся уравнением изобары Вант–Гоффа (61).

Анализ уравнения изобары Вант-Гоффа показывает, что характер зависимости константы равновесия от температуры определяется знаком теплового эффекта. Возможны 3 случая:

1) > 0 – для эндотермических реакций, т.е. реакций, протекающих с поглощением теплоты. Отсюда, зависимость константы равновесия от температуры будет возрастающей, т.е. с ростом температуры константа равновесия будет увеличиваться.

2) < 0 – для экзотермических реакций, т.е. реакций, протекающих с выделением теплоты. Отсюда, зависимость константы равновесия от температуры будет убывающей, т.е. с ростом температуры константа равновесиябудет уменьшаться.

3) Если  0, то , следовательно, константа равновесия от температуры не зависит.

Для рассматриваемой реакции = –91,88 кДж, т.е. реакция является экзотермической, следовательно, выполняется условие (2). Поэтому с ростом температуры константа равновесия будет уменьшаться. Это согласуется с величинами констант равновесия при температурахТ= 298 К иТ= 800 К (см. решение задачи № 18).

б) Для оценки влияния давления воспользуемся уравнением Планка:

, (64),

где – изменение числа молей газообразных веществ в ходе реакции. Проанализируем уравнение Планка:

1) Если реакция идет с увеличением числа молей газообразных веществ, , то, т.е. с ростом давления константа равновесия уменьшается.

1Для органических веществ уравнение зависимости теплоемкости от температуры С_р= а +bT+cT², для неорганических С_р= а +bT+c^//T².

59