Тема 3. Расчет характеристических термодинамических функций

Задача №9

Определите абсолютную энтропию S_T 1 моль вещества, указанного в таблице 10, при температуре Т К (табл. 6), если известны значения температур плавления и кипения этого вещества. Теплоемкости веществ в различных агрегатных состояниях возьмите из справочника.

Теплоту испарения возьмите из расчетов задачи №5.

Таблица 10

Вариант	Вещество	ТПЛ, К	ТКИП, К
1	нитрометан	244	374
2	нитроэтан	183	387
3	этиленгликоль	257	471
4	глицерин	291	563
5	диметиламин	181	280
6	ацетон	178	329
7	циклогексан	280	354
8	этилацетат	189	350
9	пропанол-1	147	370
10	этанол	158	351
11	амиловый спирт	194	411
12	муравьиная кислота	281	374
13	хлороформ	209	334
14	анилин	267	457
15	диэтиловый эфир	157	308
16	пиридин	231	389

Продолжение таблицы 10

Вариант	Вещество	ТПЛ, К	ТКИП, К
17	валериановая кислота	244	450
18	толуол	178	384
19	октан	216	399
20	муравьиная кислота	281	374
21	бутанол	193	391
22	хлорметан	174	297
23	пентан	143	309
24	уксусная кислота	290	391
25	нитробензол	279	484
26	хлорбензол	228	405
27	м-ксилол	225	412
28	нитроглицерин	286	398
29	1,4-диоксан	285	374
30	бензол	279	353

Решение:

Определим абсолютную энтропию 1 моль воды при температуре минус 70⁰ С.

Абсолютное значение энтропии позволяет определить третье начало термодинамики или теорема Нернста: при абсолютном нуле энтропия правильного кристалла любого чистого вещества равна нулю (эту формулировку теоремы Нернста предложил М.Планк).

S₀ = 0 при Т = 0.

Абсолютную энтропию вещества при температуре Т рассчитывают, используя постулат Планка, а также значения теплоемкостей, температур фазовых переходов и теплот фазовых переходов в интервале от 0 К до Т. На практике для расчета абсолютной энтропии при температуре Т используют справочные данные об абсолютных энтропиях веществ при 298 К. При расчете вносится поправка, учитывающая изменение энтропии вещества в интервале от 298 К до Т.

.

По условию задачи необходимо определить энтропию при температуре минус 70⁰ С, т.е. при 203 К, следовательно, к значению необходимо прибавить изменение энтропии в интервале температур от 298 до 203 К.

В заданном интервале температур вода претерпевает фазовое превращение – плавление при 273 К. Расчет энтропии проводится по аддитивной схеме:

. (31)

В справочнике найдем абсолютную энтропию воды при 298 К.

= 69,95 Дж/(моль∙К).

Изменение энтропии при нагревании и плавлении определим по формулам:

, (32)

, (33)

, (34)

где n – число молей вещества; по условию задачи n = 1.

Теплоту кристаллизации воды найдем по справочнику:

H^о_{плавления} = 6000 Дж/моль. H^о_крист. = - H^о_{плавления} = -6000 Дж/моль.

Примечание: теплоту плавления для органических веществ рассчитайте по формуле = 54,4 ± 12,6 Дж/(моль·К).

-21,98 Дж/К.

Изменение температуры жидкости равно 25 градусов. Температурный интервал невелик, и можно пренебречь зависимостью теплоемкости жидкой воды от температуры. Для расчетов воспользуемся средним значением теплоемкости; по справочнику

= 75,3 Дж/(моль∙К).

Расчет в этом случае проведем по формуле:

= -6,59 Дж/К.

Для льда разность температур составляет 70 градусов. Учтем зависимость теплоемкости от температуры (коэффициенты уравнения возьмем из справочника):

= 4,41 + 109,5·10^–3Т + 46,47·10^–6Т² Дж/(моль∙К).

=

=

Рассчитаем абсолютную энтропию воды при –70⁰ С (31):

= 69,95 – 21,98 – 6,59 – 9,75 = 31,63 Дж/К.

Задача №10

Вычислите изменение энтропии в реакции, приведенной в табл. 2, при температуре T = 298 К и Т К (табл. 6).

Решение:

Определим изменение энтропии реакции при температурах 298 К и 800 К.

Выписываем из справочника абсолютные энтропии участников реакции:

Таблица 11

Вещество	S0298 , Дж/(моль·К)
N2	191,50
H2	130,52
NH3	192,66
прод	385,32
исх	583,06
, реакции	– 197,74

Изменение энтропии в ходе реакции при температуре 298 К равно разности абсолютных энтропий продуктов и исходных веществ, взятых с учетом стехиометрических коэффициентов:

. (35)

= 2·192,66 –191,50 –3·130,52 =385,32 –583,06= –197,74 Дж/К.

Изменение энтропии реакции при температуре Т рассчитывается по общей формуле:

. (36)

Для приближенного расчета можно пренебречь зависимостью теплоемкостей от температуры и воспользоваться значениями средних теплоемкостей участников реакции. В этом случае расчет ведется по формуле

. (37)

Для точного расчета необходимы данные по зависимости теплоемкостей от температуры. В этом случае изменение энтропии реакции рассчитывается по формуле:

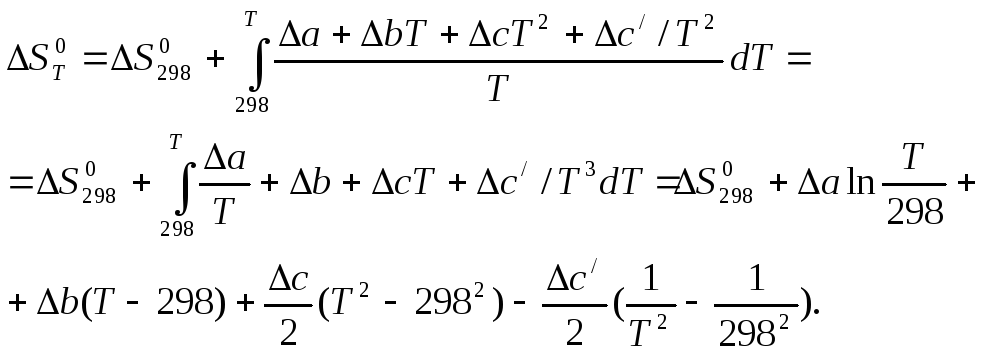(38)

Воспользуемся справочными данными и результатами расчетов из задачи №8.

Приближенно:

_{, реакции}= – 197,74 + (– 31,88) ln (800/298) = – 229,22 Дж/K.

Точно:

_{, реакции}= – 197,74 + (–50,12) ln(800/298) + 36,91·10^–3(800 – 298) +

+ 1/2(–1,50·10^–6)(800² – 298²) – 1/2(–3,34·10⁵)(1/800² – 1/298²) =

= – 230,36 Дж/K.

Задача №11

Рассчитайте изменение энтропии при смешении n₁ моль газа 1 и n₂ моль газа 2 при постоянной температуре и давлении 1 атм (табл. 12). Принять, что данные вещества подчиняются законам идеальных газов.

Таблица 12

Вариант	Газ 1	Газ 2	n1, моль	n2, моль
1	H2	N2	1	2
2	H2O	O2	5	6
3	He	CO2	1	5
4	CH4	C2H6	7	8
5	Ne	CH4	3	2,5
6	H2	He	6	7
7	CO	C2H4	3,5	4
8	CO2	N2	7	9
9	CH4	CO2	2	4
10	C2H6	Xe	3	6
11	CH4	C2H4	8	9
12	CO	CO2	9	6
13	N2	Cl2	6	8
14	H2O	N2	1	4
15	He	O2	3	1
16	N2	O2	4	5
17	F2	Ar	8	1
18	Ne	Cl2	5	7
19	Kr	CO2	7	1
20	Ar	Cl2	2	6
21	O2	H2	7	2
22	Cl2	N2	3	4
23	CO	Kr	1,5	5
24	Ar	Ne	4,5	7
25	Xe	F2	6	2,5
26	C2H4	Kr	3,5	4,5
27	CO2	F2	1,8	8
28	C2H4	Ne	6	7,5
29	CH4	Ar	5	4,5
30	Kr	Cl2	2	8,5

Решение:

Рассчитаем изменение энтропии при смешении двух молей азота (газ 1) и трех молей водорода (газ 2) при постоянной температуре и давлении 1 атм.

В случае смешения идеальных газов процесс можно представлять как изотермическое расширение каждого из газов до общего объема. При изотермическом расширении

, (39)

где n – число молей газа, V_{начальн} – начальный объем газа, V_конечн – конечный объем, который в данном случае (при р = const) равен сумме начальных объемов обоих газов.

Для газа 1

,

так же можно выразить S₂. Следовательно,

S_смеш = S₁ + S₂ = . (40)

Парциальный объем идеального газа пропорционален его мольной доле в смеси. Мольная доля газа в смеси рассчитывается по формуле:

. (41)

Выразим мольную долю газа 1 в смеси

,

и газа 2 –

,

Тогда изменение энтропии при смешении двух газов можно рассчитать по формуле

S_смеш = –R() (42)

S_смеш = –8,314() = 27,98 Дж/К.

Так как ∆S>0 процесс смешения газов протекает самопроизвольно.

Задача №12

В изолированной системе при Т = 298 К 1 моль идеального газа обратимо изотермически сжимается от давления p₁=1,0133·10⁵ Па до p₂ (табл. 13). Вычислить значения работы расширения А, теплоты Q, изменения внутренней энергии U, энтальпии H, энтропии S, энергии Гиббса G и энергии Гельмгольца F системы. Определить направление самопроизвольного процесса.

Таблица 13

Вариант	p2∙10–5, Па	Вариант	p2∙10–5, Па	Вариант	p2∙10–5, Па
1	1,019	11	1,925	21	4,035
2	1,722	12	2,064	22	6,900
3	1,317	13	8,100	23	4,125
4	3,039	14	5,066	24	1,310
5	1,823	15	1,330	25	1,423
6	1,519	16	1,365	26	1,805
7	1,215	17	1,578	27	2,148
8	4,053	18	3,520	28	1,516
9	2,533	19	2,345	29	2,045
10	5,066	20	3,543	30	1,790

Решение:

Определим изменение характеристических термодинамических функций при обратимом изотермическом сжатии 1 моль идеального газа от p₁=1,0133·10⁵ Па до p₂=1,0133·10⁶ Па.

При изотермическом сжатии идеального газа изменение внутренней энергии ∆U = 0 и изменение энтальпии ∆H = 0. Поэтому из формулы (5)

.

Работа изотермического сжатия от p₁ до p₂ определяется по формуле:

. (43)

A =Q = 1∙8,314∙298∙ln(1,0133·10⁵/1,0133·10⁶ )= – 5698,42 Дж.

Изменение энтропии в изотермическом процессе определяется по формуле

. (44)

1∙8,314 ∙ln(1,0133·10⁵ /1,0133·10⁶ )= – 19,12 Дж/К.

Изменение состояния системы выражается через изменение энергии Гельмгольца ∆F и изменение энергии Гиббса ∆G:

(V = const, T = const); (45);

(p = const, T = const); (46).

∆F= 0 – 298 ∙(–19,12) = 5697,76 Дж.

∆G= 0 – 298 ∙(–19,12) = 5697,76 Дж.

Так как процесс протекает в изолированной системе, критерием направленности самопроизвольного процесса является изменение энтропии. Если ∆S > 0, процесс самопроизвольно идет в прямом направлении. По расчету ∆S < 0, следовательно, процесс идет самопроизвольно в обратном направлении.

Задача №13

Определите, осуществима ли при постоянном давлении 1 атм и температуре Т = 298 К реакция, приведенная в табл. 2.

Решение:

Определим, осуществима ли при постоянном давлении 1 атм и температуре Т = 298 К реакция .

В изобарно-изотермических условиях (p = const, T = const) на вопрос о возможности протекания самопроизвольного процесса отвечает функция Гиббса. Если изменение энергии Гиббса для реакции меньше нуля (< 0) – реакция самопроизвольно протекает в прямом направлении, если больше нуля (> 0) – в обратном направлении.

Вариант а) Определить при 298 К можно непосредственно по справочным данным о значениях всех участников реакции.

. (47)

= – 16,48 кДж/моль;

= 0 кДж/моль;

= 0 кДж/моль.

= 2· –3· –

= 2·(– 16,48) = – 32, 96 кДж.

Вариант б) Если известны тепловой эффект реакции и изменение энтропии в ходе реакции, то расчет можно вести по формуле:

. (48)

= – 91,88 кДж (см. задачу №2),

= – 197,74 Дж/К (см. задачу №10).

= – 91880 – 298·(–197,74) = – 32953,5 Дж.

Так как < 0, реакцияпри 1 атм и температуреТ = 298 К осуществима, т.е. самопроизвольно протекает в прямом направлении.

Задача №14

Вычислите изменение энергии Гиббса (ΔG⁰) при нагревании 1 моля вещества (при постоянном давлении 1 атм), приведенного в табл. 14, от Т₁ до Т₂ К.

Таблица 14

Вариант	Вещество	Т1, К	Т2, К
1	нитрометан	245	300
2	нитроэтан	288	350
3	этиленгликоль	275	300
4	глицерин	268	400
5	диметиламин	298	450
6	ацетон	278	500
7	циклогексан	280	550
8	этилацетат	258	600
9	пропанол-1	268	650
10	этанол	313	700
11	амиловый спирт	280	750
12	муравьиная кислота	293	800
13	хлороформ	333	850
14	анилин	310	900
15	диэтиловый эфир	281	950

Продолжение таблицы 14

Вариант	Вещество	Т1, К	Т2, К
16	пиридин	278	1000
17	валериановая кислота	263	950
18	толуол	276	900
19	октан	290	850
20	муравьиная кислота	300	800
21	бутанол	280	750
22	хлорметан	299	700
23	пентан	292	650
24	уксусная кислота	288	600
25	нитробензол	308	550
26	хлорбензол	296	500
27	м-ксилол	291	450
28	нитроглицерин	308	400
29	1,4-диоксан	242	350
30	бензол	205	300

Решение:

Вычислим ΔG⁰ при нагревании 1 моля NH₃ от T₁ = 300 К до T₂ = 400 К при постоянном давлении Р = 1 атм.

Вариант а) Изменение свободной энергии Гиббса в процессе нагревания вещества может быть определено из соотношения

= —S. (49)

При p = const

dG = —SdT,

. (50)

Расчет можно вести с различной степенью точности.

Вариант а) Приближенный расчет, без учета зависимости энтропии от температуры проводится по уравнению

, (51)

которое получается после интегрирования уравнения (50) при условии S = const.

По справочным данным абсолютная энтропия аммиака при 298 К = 192,66 Дж/моль·К.

–192,66·(400 – 300) = – 19266 Дж.

Вариант б) Более точный расчет можно провести, учитывая, что энтропия зависит от температуры. Для этого необходимо вывести уравнение зависимости S = f(T). Учтем, что

. (52)

Если пренебречь зависимостью теплоемкости от температуры и проинтегрировать уравнение (52), считая =const, тогда получим

.

Тогда из уравнения (50)

G⁰ = –,

,

G⁰ = – ( (T₂ – T₁) + T₂ lnT₂ – T₁ lnT₁ – (T₂ – T₁) –

– T₂ ln298 + T₁ ln298) = – (( -)(T₂ – T₁) +

+ T₂ (lnT₂ – ln298)+ T₁ (ln298 – lnT₁),

G⁰ = ( – )(T₂ – T₁) – (T₂ ln T₁ ln). (53)

Полученной формулой можно пользоваться для приближенного подсчета в небольшом интервале температур при условии =const.

По справочным данным средняя теплоемкость аммиака в данном интервале температур = 35,16 Дж/(моль·К), абсолютная энтропия аммиака при 298 К = 192,66 Дж/(моль·К).

= (35,16 – 192,66)(400 – 300) – 35,16·400·ln+

+ 35,16·300·ln= – 19796 Дж.

Вариант в) Точный расчет, с учетом того, что теплоемкость является функцией температуры.

По справочным данным зависимость теплоемкости аммиака от температуры выражается уравнением:

С_{р NH3} = 29,80 + 25,48·10^–3 T – 1,67·10⁵/T².

Выведем зависимость энтропии от температуры с учетом зависимости теплоемкости от температуры:

= =

= + a^.lnT/298 + b(T – 298) – с^//(2^.Т²) + с^//(2^.298²).

Подставляя справочные данные, получим уравнение

= 192,66 + 29,80 lnT – 29,80 ln298 + 25,48·10^–3 T –

– 25,48·10^–3·298 + 1,67·10⁵/(2·Т²) –1,67^.10⁵/(2^.298²);

= 14,12 + 29,80 lnT + 25,48·10^–3 T + 0,835·10⁵/Т².

Подставим полученное уравнение в формулу для расчета функции энергии Гиббса (50):

= –(14,12 + 29,80 lnT + 25,48·10^–3 T + 0,835·10⁵/Т²)dT,

= – (14,12T + 29,80·T·lnT – 29,80T + 25,48/2·10^–3 T² –

– 0,835·10⁵/Т) ,

= – (14,12(400 – 300) + 29,80·400·ln400 – 29,80·300·ln 300 –

– 29,80(400 – 300) + 12,74·10^–3 (400² – 300²) – 0,835·10⁵(1/400 –

– 1/300)) = – 19819 Дж.

Вариант г) Расчет с использованием приведенных функции энергии Гиббса

, (54)

, (55)

, (56)

= 400·Ф₄₀₀ + Н₀⁰ – 300·Ф₃₀₀ – Н₀⁰ = 400·Ф₄₀₀ – 300·Ф₃₀₀.

В справочнике отсутствует значение Ф₄₀₀, найдем его путем интерполирования:

Ф₂₉₈= –158,98Дж/(моль·К),Ф₅₀₀ = – 176,82 Дж/(моль·К)

Ф₄₀₀ = –158,98 –8,92 = – 167,9 Дж/(моль∙К).

= 400·(–167,9) – 300·(–158,98) = – 19466 Дж.