21. Скорость звука

Скорость звука – скорость распространения в упругой среде малых возмущений. Малыми или слабыми принято называть такие возмущения среды, в которых местное изменение давления среды в точке возмущения, т.е. амплитуда давления, пренебрежимо мало по сравнению с общим давлением. Понятие скорости звука является одним из важнейших в теории течения сжимаемой жидкости.

Р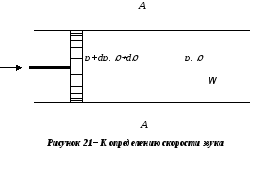ассмотрим процесс распространения малого (слабого) возмущения в сжимаемой среде. Пусть неподвижная сжимаемая жидкость с заданными параметрами p, находится в длинной трубе постоянного по длине сечения, ограниченной слева поршнем (см. рис.21). В некоторый момент времени поршень начинает двигаться слева направо с постоянной скоростьюWи «наталкивается» на неподвижную жидкость. «Слой» жидкости, непосредственно примыкающий к поршню, в результате движения поршня несколько уплотняется (сжимается) и давление в нем повышается – до величиныp+dp;кроме того, жидкость в этом «слое» из состояния покоя приходит в движение со скоростьюW.Далее сжимается и приходит в движение «слой» жидкости, примыкающий к «первому слою», и т.д. Можно представить себе движущуюся в жидкости«слабую волну сжатия», подобную той, которая возникает при трогании с места длинного железнодорожного состава – вагоны не одновременно, а последовательно (поочерёдно) приходят в движение благодаря упругости сцепки. Другим примером может служить картина падающих костяшек домино, выстроенных в длинный ряд.

Таким образом, в жидкости распространяется слабая волна сжатия, фронт которой можно представить в виде перемещающегося вдоль трубы (точнее - вдоль жидкости) сечения А-А, отделяющего сжатую – «возмущённую», область жидкости с параметрамиp+dp, d, T+dT(слева от сеченияА-А) от невозмущённой области жидкости, т.е. области, куда возмущения ещё не проникли (справа от сеченияА-А). Если перемещение сеченияА-Аза времяdt обозначитьdx, то скорость распространения фронта слабой волны в этом случае может быть выражена как dx dt.Скорость движения фронта слабой волны относительно жидкости называют скоростью звука и обозначают обычно а. «Относительность» особенно важно иметь в виду, поскольку жидкость в общем случае в момент возникновения в ней возмущения не обязательно должна находиться в состоянии покоя, а может изначально двигаться с некоторой скоростью.

За время dt фронт волны – сечениеА-А, переместится на расстояниеdx = a dt и при этом будет сжат «новый слой» жидкости, т.е. произойдет уплотнение жидкости - увеличение плотности распределения массы в элементарном объёмеdV = F dx = F a dt,заключённом между начальным и конечным в указанный промежуток времени положениями сеченияА-А. Поскольку в рассматриваемом элементарном объёмеdVнет источников и стоков, то приращение массы жидкости в этом объёме может происходить только за счет притока в него за времяdtнекоторого количества жидкости из «возмущённой» области со скоростьюW.

Очевидно, что из уравнения неразрывности для рассматриваемого случая:

dV d  (dFW dtилиF a dt d  (dFW dt,

где F– площадь поперечного сечения трубы,dV d - изменение массы жидкости в элементарном объёмеdV; (dFW dt –масса жидкости, притекающая в элементарный объёмdVза времяdt; с точностью до малых величин первого порядка (пренебрегая бесконечно малой величиной второго порядкаFW d dt)можно получить следующее соотношение:

a d  W. (1)

Применим к рассматриваемому элементарному объёму dV закон о сохранении количества движения, не учитывая при этом действия сил трения в жидкости (допустим, что жидкость идеальная). Изменение количества движения элементарного объёмаd(mW) (здесьm – масса элементарного объёма) должно быть равно импульсу внешних сил, приложенных к этому объёму. В рассматриваемом случае в качестве внешних сил выступает только поверхностная сила, обусловленная разностью (градиентом) давления в звуковой волнеdp.Заменяя массу произведением плотности на объём, и учитывая, что скорость движения рассматриваемого объёма в начальный момент времени (до прохождения через него фронта волны) была равна нулю, получим уравнение движения (уравнение количества движения) для рассматриваемого элементарного объёма:

(dF aW dt  F dp dt,

где слева стоит приращение количества движения элемента, а справа – импульс сил, действующих на элемент за время dt.Из уравнения движения, рассуждая аналогично предыдущему (пренебрегая бесконечно малой величиной второго порядкаF aW d dt),получим ещё одно соотношение

aW  dp. (2)

Исключив из полученных соотношений (1) и (2) скорость W, получим уравнение для определения скорости звука:

. (3)

Для того чтобы воспользоваться уравнением (3) нужно знать, как происходит процесс распространения звуковых волн, т.е. для каких условий следует вычислять производную dp/d.

Одним из первых, кто практически решил эту задачу, был Исаак Ньютон. Он вычислил скорость звука в воздухе при атмосферном давлении и комнатной температуре (при этих параметрах воздух с хорошим приближением можно рассматривать как совершенный газ, для которого справедливо уравнение состояния p=RT). Ньютон считал, что процесс распространения звука в воздухе происходит в изотермических условиях и производную надо брать при постоянной температуре, т.е. при условииT=const.Воспользовавшись уравнением Бойля-Мариотта для изотермического процесса в совершенном газеpv= const илиp=const, для производной получим

,

а для скорости звука

. (4)

Однако при прямых измерениях скорости звука в воздухе было получено значение апримерно на 20% превосходящее величину, вычисленную Ньютоном. Причина этих расхождений была установлена Лапласом, который отметил, что поскольку звуковые колебания (волны) в упругой среде (воздухе) распространяются очень быстро, то можно предположить, что сколь-нибудь заметного теплообмена между зонами разряжения и сжатия звуковой волны и окружающей средой при этом не успевает произойти (что, кстати, хорошо подтверждается опытом). Поэтому, процесс распространения звуковой волны можно считать адиабатным и изоэнтропийным и производную в (3) нужно брать при постоянной энтропии, т.е. при условииS=const.

Уравнение Лапласа для скорости звука

. (5)

В случае изоэнтропийного процесса плотность и давление будут связаны уравнением изоэнтропы p^ =const.

Тогда dp = ^- dconst иdp/d   ^-const,

определяя постоянную из уравнения изоэнтропы, для производной (p/)_S получим

, (6)

а для скорости звука

. (7)

Для совершенного газа, имея в виду, чтоp = RT, может быть установлена однозначная связь скорости звука с абсолютной температурой газа

. (8)

Из соотношения (8) видно что, чем выше температура газа, тем больше скорость распространения звуковых волн в нём. Кроме того, скорость звука зависит от физических свойств газа ( иR). Этот вывод находится в полном соответствии с газокинетическими представлениями о процессе распространения малых возмущений в среде, состоящей из движущихся молекул. Скорость распространения возмущений должна зависеть от скорости движения молекул, которая, в свою очередь, определяется температурой. Известно, что скорость движения молекул газа (средняя скорость) близка к скорости звука. В этой связи необходимо подчеркнуть, что квадрат числа МахаM²=W²/a²определяет соотношение в потоке средней кинетической энергии направленного движения газа как целого и средней кинетической энергии беспорядочного движения молекул, т.е. частиц, составляющих это целое.

Следует иметь в виду, что формула (7), как и уравнение Лапласа (5) справедливы и для газов и для капельных жидкостей и для твердых упругих тел, в то время как формула (8) имеет отношение только к совершенному газу.

В несжимаемыхсредах = const, d = 0иa=,т.е. звуковые волныраспространяются мгновенно.