Мы получили, что

Отсюда видно,что длительность события, происходящего в некоторой точке, будет наименьшей в той инер­циальной системе отсчета, относительно которой эта точка неподвижна. Например, часы, дви­жущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в той системе отсчета, относительно которой они движутся. Это замедление становится заметным при скоростях, близких к ско­рости света.

Эффект замедления хода времени подтверждается экспериментально в опытах с мюонами – нестабильными элементарными частицами. Среднее собственное время жизни мюона (по часам в той инерциальной системе отсчета, относительно которой он покоится) τ₀ =2,2 мкс. Мюоны рождаются в верхних слоях атмосферы под действием первичного космического излучения и движутся относительно Земли со скоростями, близкими к скорости света. Если бы релятивистского эффекта замед­ления хода времени не было, то по отношению к земному наблюдателю мюон мог бы за время своей жизни пройти путь в атмосфере, не превышающий в среднем τ₀с = 660 м. Иными словами, мюоны не могли бы достигать поверхности Земли. В дейст­вительности, мюоны регистрируются приборами, установленными на поверхности Земли, так как среднее время движущегося мюона по часам земного наблюдателя много больше τ₀ и путь, проходимый мюоном за это время много больше 660 м.

4. Релятивистский закон сложения скоростей.

Рассмотрим движение материальной точки в системе К’ со скоростью u. Определим скорость этой точки в системе К если система К’ движется со скоростью v. Запишем проекции вектора скорости точки относительно систем К и К’:

K: u_x=dx/dt, u_y=dy/dt, u_z=dz/dt; K’: u_x’=dx’/dt’, u_y’ =dy’/dt’, u’_z=dz’/dt’.

Теперь нам нужно найти значения дифференциалов dx, dy, dz и dt. Продифференцировав преобразования Лоренца, получим:

,,,.

Теперь мы сможем найти проекции скорости:

, ,.

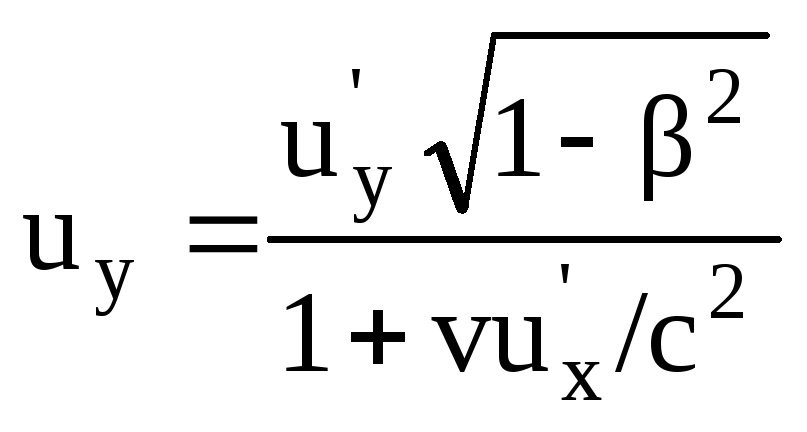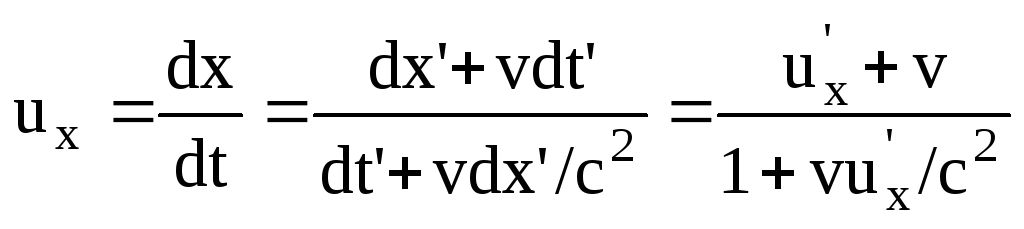Из этих уравнений видно, что формулы, связывающие скорости тела в разных системах отсчета (эаконы сложения скоростей) существенно отличаются от законов классической механики. При скоростях малых по сравнению со скоростью света, эти уравнения переходят в классические уравнения сложения скоростей.

6. 5. Основной закон динамики релятивистской частицы. @

Масса релятивистских частиц, т.е. частиц, движущихся со скоростями v ~ с не постоянна, а зависит от их скорости: . Здесьm₀ – это масса покоя частицы, т.е. масса, измеренная в той системе отсчета, относительно которой частица покоится. Эта зависимость подтверждена экспери­ментально. На основании ее рассчитывают все современные ускорители заряженных частиц (циклотрон, синхрофазотрон, бетатрон и т.д.).

Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к дру­гой, следует условие инвариантности физических законов относительно преобразо­ваний Лоренца. Основной закон динамики Ньютона F=dP/dt=d(mv)/dt оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса .

Основной закон релятивистской динамики имеет вид:       ,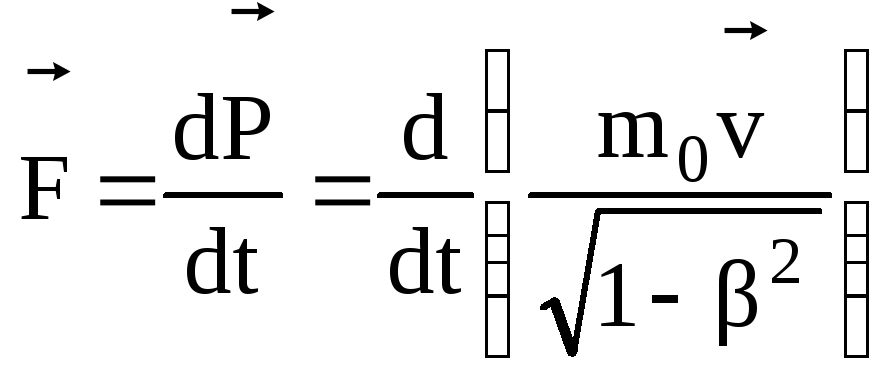

и формулируется следующим образом: скорость изменения релятивистского импульса частицы, движущейся со скоростью близкой к скорости света, равна дей­ствующей на нее силе. При скоростях, намного меньших скорости света, полученное нами уравнение переходит в основной закон динамики классической механики. Основной закон релятивистской динамики инвариантен по отношению к преобразованиям Лоренца, но можно показать, что ни ускорение, ни сила, ни импульс сами по себе ин­вариантными величинами не являются. В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы не изменяется с течением времени.

Кроме всех перечисленных особенностей, основной и важнейший вывод специальной теории относительности сводится к тому, что пространство и время органически взаимосвязаны и образуют единую форму суще­ствования материи.