5. Волновые процессы@

5.1. Понятие о волнах. Виды волн.@

Если какую-либо частицу упругой среды заставить колебаться, то благодаря взаимодействию между частицами, соседние частицы тоже начнут колебаться, такой процесс вовлечения частиц в колебательное движение будет охватывать со временем все большее число частиц. Процесс рас­пространения колебаний в среде называется волновым процессом или волной. В таком процессе сами частицы среды не перемещаются на большие расстояния, они только совершают колебания около положений равновесия, причем частицы в разных точках ко­леблются с некоторым сдвигом по фазе.

Различают поперечные и продольные волны. Волна называется поперечной, если колебания частиц среды происходят в направлении, перпен­дикулярном к направлению распространения волны. Примеры поперечных волн: распространение колебаний атомов в узлах кристаллической решетки твердого тела, колебания величин электрического и магнитного полей при распространении электромагнитных волн, волны на поверхности воды и т.д. Волна называется продольной, если колебания частиц среды происходят около положений равновесия вдоль направления распространения волны. Примеры продольных волн: колебания в пружинных системах, распространение колебаний атомов в газах и жидкостях (распространение звуковых волн), такие колебания также возникают и в твердых телах.

Волны также делят по виду волновых поверхностей на плоские, сферические и др. Волновая поверхность  ‑ это геометрическое место точек в пространстве, в которых колебания происходят одинаковым образом или в одной фазе. Для плоских волн волновые поверхности представляются параллельными плоскостями или линиями, для сферических волн – сферами или окружностями с общим центром (Рис.5.1). Волновые поверхности неподвижны. Поверх­ность, к которым подошли колебания в какой то момент времени и которая отделяет колеблющиеся частицы от ещё не ко­леблющихся частиц, называется фронтом волны.

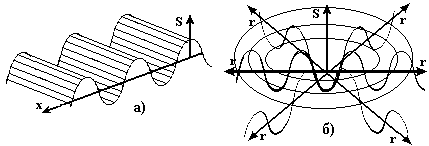
Рис.5.1.а) Плоская волна, б) Сферическая волна.

5.2. Волновое уравнение. Уравнения и характеристики волн. @

Е

Рис.5.2. Смещение частиц среды в бегущей волне.

сли волна распространяется вдоль некоторого направления, то смещение частицы от положения равновесияS будет зависеть от времени t и от местоположения частицы х или r. Дифференциальное уравнение для волны имеет вид и называется волновым уравнением, здесьv – скорость распространения волны. Решение такого уравнения имеет вид:

для плоской волны ,  а для сферической. Графически такие волны изображают синусоидами, которые смещаются со временем (Рис.5.2), поэтому такие волны (в отличие от стоячих) называют бегущими волнами, хотя сами частицы вещества никуда не бегут, а колеблются около своего постоянного положения равновесия.

Новыми характеристиками, по сравнению с простыми колебаниями, являются фазовая скорость v, длина волны, волновое число. Фазовой скоростью или скоростью распространения волны v называют скорость перемещения фазы или точек пространства, где колебания находятся в одной фазе, например точек амплитудного значения А. Эта скорость равна скорости перемещения волнового фронта или скорости распространения волнового процесса. Длиной волны называют расстояние, на которое распространяется волновой процесс за время равное периоду колебаний Т (  vT) или кратчайшее расстояние между частицами, колеблющихся в одной фазе. Используя эти характеристики, уравнения волн можно записать следующим образом:

для плоской волны ,  а для сферической волны, гдеk – волновое число, показывающее, сколько длин волн уложится на расстоянии в 2 метров (k = 2  v), а ‑ волновой вектор, равный по величине волновому числу и направленный вдоль вектора фазовой скорости.

5. 3. Энергия волны. Перенос энергии. @

Так как частицы среды двигаются при колебаниях и взаимодействуют между собой, то они обладают как кинетической, так и потенциальной энергией. В непрерывной среде рассматривают сумму кинетической и потенциальной энергии (механическую энергию) dE_м единицы объема dV вещества или объемную плотность энергии среды _м = dЕ_м/dV. Расчет механической энергии приводит к выражению , которое сходно с выражением для механической энергии колебаний осцилятора за исключением сомножителя, зависящего от времени. Это означает, что энергия в каждом объеме пространства меняется со временем за счет ее передачи от одной частицы к другой. Эксперименты показывают, что волны действительно переносят энергию, это относится как к механическим волнам в материальных средах, так и к электромагнитным волнам в вакууме. Процесс переноса энергии волной описывается вектором Умова‑Пойнтинга, который направлен вдоль вектора фазовой скорости и численно равен количеству переносимой энергии за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. Формула для его расчета имеет вид

.

Из этого выражения видно, что вектор Умова‑Пойнтинга тоже меняется со временем. Так как частоты реальных колебаний очень велики, то на практике обычно измеряются усредненные значения, для вектора Умова‑Пойнтинга среднее значение по времени от его модуля называют интенсивностью волнового процесса. Интенсивность волны I – это скалярная величина, показывающая количество переносимой волной энергии в среднем за единицу времени через единичную площадку, перпендикулярную к направлению движения волны. Если провести усреднение по времени одного полного колебания, то получим .Отсюда видно, что интенсивность пропорциональна амплитуде колебаний. В случае плоской волны амплитуда и интенсивность не меняются по мере распространения волны, но для сферической волны А  1/r и интенсивность убывает с расстоянием I  1/r².

5. 4. Принцип суперпозиции волн. Явление интерференции. @

Если в среде распространяется одновременно несколько волн, то результирующие колебания частиц среды зависят от воздействия отдельных волн. В линейных средах выполняется принцип суперпозиции волн, согласно которому все параметры результирующего колебания (смещение, скорость, ускорение) равны сумме соответствующих параметров отдельных волн. Линейными являются все упругие среды, в которых смещения частиц от положения равновесия подчиняются закону Гука (смещение пропорционально силе, действующей на частицу). Нарушение принципа суперпозиции может происходить при распространении волн большой интенсивности. Например, при прохождении в среде лазерных лучей, такой большой мощности, что они могут изменить упругие свойства вещества, для результирующих колебаний этот принцип не соблюдается. Такие среды называют нелинейными.

В линейных средах, вследствие выполнения принципа суперпозиции, наблюдается явление интерференции света. Явление интерференции – это явление увеличения и уменьшения амплитуды результирующих колебаний при наложении двух или более когерентных волн, колеблющихся в одной плоскости. Когерентными называют волны, разница фаз которых не меняется со временем. Для объяснения этого явления рассмотрим случай наложения в точке М₁ или М₂ двух колебаний одной частоты, идущих от источников S₁ и S₂ (Рис.5.3).

Рис.5.3. Сложение колебаний при интерференции (в точке М₁ – усиление, в точке М₂ –  ослабление колебаний).

Уравнения волн в точке М будут иметь вид и. Суммарное колебание в точке М, используя формулу для синуса разности, можно представить в виде

Последнее выражение можно рассматривать как , где

. Из этих уравнений можно определить А и  . Разделив второе уравнение на первое находим , а возведя эти уравнения в квадрат и сложив их, можно найти что, где разница фаз. Если учесть, что интенсивность пропорциональна квадрату амплитуды колебаний, то после усреднения последнего уравнения получим.

В случае сложения не когерентных волн разница фаз меняется со временем произвольным образом и среднее значение косинуса будет равно нулю и , то есть происходит обычно наблюдаемое сложение интенсивностей колебаний. Но если колебания когерентные, то разница фаз не будет меняться со временем и среднее значение косинуса не будет равно нулю. В этом случае в разных точках пространства будут различные значения суммарной амплитуды колебаний и интенсивности. В точках, для которыхи здесь будет максимальное усиление колебаний, в этих точках разница фаз должна быть равна- это условие для максимума интерференции. В точках, для которыхи здесь будет максимальное ослабление колебаний, в этих точках разница фаз должна быть равна- это условие для минимума интерференции. В точках, где не удовлетворяются эти условия, будут промежуточные значения амплитуды и интенсивности колебаний.