
- •Н.Х. Зиннатуллин
- •1. Введение
- •Предмет и задачи дисциплины
- •Классификация основных процессов химической технологии
- •Гипотеза сплошности среды
- •Режимы движения жидких сред
- •Силы и напряжения, действующие в жидких средах
- •I – часть
- •2.1.2. Механизмы переноса субстанций
- •Молекулярный механизм
- •Конвективный механизм
- •Турбулентный механизм
- •Рис 2.2. Схема осреднения скорости
- •2.1.3. Условие проявления и направление процессов переноса
- •2.1.4. Уравнения переноса субстанций
- •2.1.4.1. Перенос массы Молекулярный механизм переноса массы
- •Конвективный механизм переноса массы
- •Турбулентный механизм переноса массы
- •2.1.4.2. Перенос энергии
- •Молекулярный механизм переноса энергии
- •Конвективный механизм переноса энергии
- •Конвективный перенос импульса
- •Турбулентный перенос импульса
- •2.1.5. Законы сохранения субстанций
- •2.1.5.2. Закон сохранения энергии
- •Интегральная форма закона сохранения энергии (первый закон термодинамики)
- •Локальная форма закона сохранения энергии
- •2.1.5.3. Закон сохранения импульса
- •Интегральная форма закона сохранения импульса
- •Локальная форма закона сохранения импульса
- •2.1.6. Исчерпывающее описание процессов переноса
- •2.1.6.1. Условия однозначности
- •2.1.6.2. Поля скорости, давления, температуры и концентраций Пограничные слои
- •2.1.6.3. Аналогия процессов переноса
- •2.2 Межфазный перенос субстанции
- •2.2.1. Уравнения массо-, тепло- и импульсоотдачи
- •2.2.1.1. Локальная форма уравнений
- •Рис 2.5. Перенос субстанций по оси z
- •2.2.1.2. Интегральная форма уравнений
- •Рис 2.6. Изменение температуры в ядре потока по длине аппарата для различных моделей
- •2.2.2 Уравнения массо-, тепло- и импульсопередачи
- •2.2.2.1 Локальная форма уравнений
- •Рис 2.7. Схема межфазного переноса субстанций.
- •Рис 2.8. Профили химических потенциалов, температуры и скорости в процессах переноса субстанций через границу раздела фаз
- •2.2.2.2 Интегральная форма уравнений
- •2.3. Моделирование технологических процессов
- •2.3.1. Математическое моделирование
- •2.3.2. Физическое моделирование
- •2.3.2.1. Теория подобия
- •2.3.2.2. Подобие гидромеханических процессов
- •2.3.2.3 Подобие тепловых процессов
- •2.3.2.4 Подобие массообменных процессов
- •2.3.3 Определение коэффициентов массо-, тепло-, импульсоотдачи
- •2.3.4 Аналогия процессов массо-, тепло-. Импульсоотдачи
- •2.3.5 Проблема масштабного перехода для промышленных аппаратов
- •2.3.6 Понятие о сопряженном физическом и математическом моделировании
- •2.4 Гидродинамическая структура потоков
- •2.4.1 Характеристика структуры потока
- •2.4.2 Математическое моделирование структуры потоков
- •2.4.2.1 Модель идеального вытеснения (мив)
- •2.4.2.2 Модель идеального смешения (мис)
- •2.4.2.3 Ячеечная модель (мя)
- •2.4.2.4 Диффузионная модель (мд)
- •2.4.3 Идентификация модели
- •Оглавление
Конвективный механизм переноса массы
Поток
массы за счет конвективного механизма
связан с конвективной скоростью
![]() :
:
![]()
![]() =
=
![]()
![]() .
.![]() (2.12)
(2.12)
В случае многокомпонентной среды можно рассмотреть поток массы для каждого компонента:
![]() , (2.13.)
, (2.13.)
где
i
– номер компонента;
![]() -
плотность компонентаi.
-
плотность компонентаi.
Зачастую удобнее использовать поток вещества, а не массы:
![]() ,
,
![]() (2.14.)
(2.14.)
где
![]() - мольная масса компонентаi,
ci
– мольная концентрация.
- мольная масса компонентаi,
ci
– мольная концентрация.
Турбулентный механизм переноса массы
Турбулентный перенос массы можно рассматривать по аналогии с молекулярным как следствие хаотичного перемещения вихрей. Вместо коэффициента молекулярной диффузии вводится коэффициент турбулентной диффузии Dт и поток массы i-го компонента за счет турбулентной диффузии записывается в виде:
![]() . (2.15.)
. (2.15.)
Если учесть, что молекулярная диффузия сохраняется и при турбулентной диффузии можно записать:
![]() =
- (Di+Dт)
=
- (Di+Dт)
![]() . (2.16.)
. (2.16.)
Поскольку объем среды, участвующие в турбулентных пульсациях, значительно превышают молекулярные размеры, интенсивность турбулентного переноса массы в пристенной области существенно выше молекулярного:
![]() ,
,
При конвективном движении среды поток массы (или вещества) определяются как суммы конвективного и молекулярного переноса, а при турбулентном режиме к ним добавляют и турбулентную составляющую.
2.1.4.2. Перенос энергии
Полную энергию системы на единицу массы можно записать:
![]() ,
,
![]() (2.17.)
(2.17.)
где
![]() - внутренняя энергия системы,
- внутренняя энергия системы,![]() - кинетическая энергия системы,
- кинетическая энергия системы,![]() - потенциальная энергия системы.
- потенциальная энергия системы.
Энергия может передаваться в виде теплоты или работы.
Теплота – форма передачи энергии на микроуровне.
Работа – форма передачи энергии на макроуровне.
Молекулярный механизм переноса энергии
Молекулярным механизмом перенос энергии осуществляется в форме тепла. Поток тепла за счет молекулярного механизма в условиях механического и концентрационного равновесия может быть представлен в виде:
![]() ,
,
![]() (2.18.)
(2.18.)
где
![]() - коэффициент молекулярной теплопроводности,
- коэффициент молекулярной теплопроводности,![]() - градиент температуры. Это уравнение
носит название закона Фурье.
- градиент температуры. Это уравнение
носит название закона Фурье.
В общем случае в плотных газах и жидкостях поток тепла будет определяться поступательным переносом кинетической и потенциальной энергии молекул, а также столкновительным переносом:
![]() .
.
Порядок
![]() для газов
для газов![]() ,
,![]()
жидкостей
![]() ,
,![]()
металлов
![]() .
.![]()
Конвективный механизм переноса энергии
Поток энергии, переносимый движущимся макроскопическим объемом за единицу времени через единицу поверхности, можно записать:
![]() . (2.19.)
. (2.19.)
Турбулентный механизм переноса энергии
Турбулентный перенос энергии можно рассмотреть по аналогии с молекулярным, вводя коэффициента турбулентной теплопроводности:
![]() . (2.20.)
. (2.20.)
Коэффициент
турбулентной теплопроводности ![]() определяется свойствами системы и
режимом движения среды.
определяется свойствами системы и
режимом движения среды.
Суммарный поток энергии при конвективном движении складывается из молекулярного и конвективного переноса, а при турбулентном движении из молекулярного, конвективного и турбулентного переноса:
![]() . (2.21.)
. (2.21.)
2.1.4.3. Перенос импульса
В рассмотренных выше явлениях переноса массы и энергии переносимые субстанции являлись скалярными величинами, а поток скалярной величины есть вектор. Импульс сам векторная величина, а ее поток будет обладать большей размерностью, а именно, представлять собой тензор второго ранга, для задания которого представляется уже 9 чисел.
Молекулярный перенос импульса

Рис 2.3. Схема молекулярного переноса импульса
Рассмотрим
движение по оси x.
Скорость
![]() меняется
по осиz
(рис.2.3.). Молекулы, переходя из области
с большими скоростями, в область а
меньшими скоростями, будут переносит
импульс, ускоряющий движение в направлении
оси x
и наоборот.
меняется
по осиz
(рис.2.3.). Молекулы, переходя из области
с большими скоростями, в область а
меньшими скоростями, будут переносит
импульс, ускоряющий движение в направлении
оси x
и наоборот.
Количество
движения по оси x
![]() ,
переносимое вдоль осиz
за единицу времени через единицу
поверхности можно представить как:
,
переносимое вдоль осиz
за единицу времени через единицу
поверхности можно представить как:
![]() ,
,
![]() (2.22.)
(2.22.)
где
![]() - коэффициенты динамической и кинематической
молекулярной вязкости. Это уравнение
носит название закона Ньютона. Величину
- коэффициенты динамической и кинематической
молекулярной вязкости. Это уравнение
носит название закона Ньютона. Величину![]() можно трактовать как касательную силу
вязкого трения, действующую в направлении
оси x
на единичную площадку перпендикулярную
оси z.
Тензор потока импульса за счет
молекулярного механизма называется
тензором вязких напряжений:
можно трактовать как касательную силу
вязкого трения, действующую в направлении
оси x
на единичную площадку перпендикулярную
оси z.
Тензор потока импульса за счет
молекулярного механизма называется
тензором вязких напряжений:
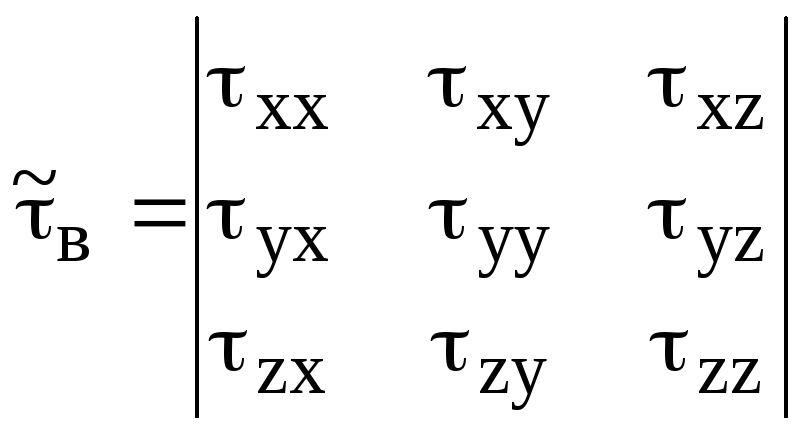 ,
где
,
где
![]() ,
,![]() ,
,![]() - нормальные
напряжения, остальные – касательные.
- нормальные
напряжения, остальные – касательные.
Все
элементы тензора вязких напряжений
потока импульса можно объяснить
аналогично выше рассмотренному
![]() .
.
