5.4. Погрешность интерполяции

Погрешность интерполяции полиномом Лагранжа оценивается по формуле:

, (5.22)

где

, (5.23)

. (5.24)

Погрешность интерполяции полиномом Ньютона оценивается по формулам:

, (5.25)

. (5.26)

5.5. Сплайн-интерполяция

При большом количестве узлов интерполяции приходится использовать интерполяционные полиномы высокой степени, что создает определенные неудобства при вычислениях. Можно избежать высокой степени интерполяционного многочлена, разбив отрезок интерполяции на несколько частей с построением на каждой части самостоятельного интерполяционного многочлена. Однако такое интерполирование обладает существенным недостатком: в точках сшивки разных интерполяционных полиномов будет разрывной их первая производная, поэтому для решения задачи кусочно-линейной интерполяции используют особый вид кусочно-полиномиальной интерполяции  сплайн-интерполяцию.

Сплайн  это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными.

Пусть интерполируемая функция f(x) задана своими значениями в узлах , . Обозначим длину частичного отрезка . Будем искать кубический сплайн на каждом из частичных отрезков в виде:

, (5.27)

где  четверка неизвестных коэффициентов. Можно доказать, что задача нахождения кубического сплайна имеет единственное решение.

Потребуем совпадения значений в узлах с табличными значениями функции :

, (5.28)

. (5.29)

Число этих уравнений (2n) в два раза меньше числа неизвестных коэффициентов. Для того чтобы получить дополнительные условия, потребуем также непрерывности первой и второй производных сплайна во всех точках, включая узлы. Для этого следует приравнять левые и правые производные ,,,во внутреннем узле.

Вычислив выражения для производных ,последовательным дифференцированием (5.27):

, (5.30)

, (5.31)

найдем правые и левые производные в узле:

,

,

где .

Аналогично поступаем для второй производной:

,

.

Приравняв левые и правые производные, получаем:

, (5.32)

, (5.33)

где .

Уравнения (5.32), (5.33) дают еще 2(n1) условий. Для получения недостающих уравнений накладывают требования к поведению сплайна на концах отрезка интерполяции. Если потребовать нулевой кривизны сплайна на концах отрезка интерполяции (т.е. равенство нулю второй производной), то получим:

, (5.34)

Исключив из уравнений (5.28)(5.33) n неизвестных , получаем систему уравнений:

(5.35)

где .

Система (5.35) состоит из 3n уравнений. Решив систему (5.35), получаем значения неизвестных , определяющих совокупность всех формул для искомого интерполяционного сплайна

(5.36)

где .

Программа, реализующая метод сплайн-интерполяции оказывается достаточно громоздкой, поэтому мы ограничимся обсуждением решения задачи об интерполяции синуса с помощью сплайнов, используя функции пакета MathCAD: interp(VS,x,y,z), lspline(x,y), pspline(x,y), cspline(x,y).

Документ пакета MathCAD, содержащий решение задачи сплайн-интерполяции, состоит из следующих блоков.

1. Задание табличных значений интерполируемой функции

2. Вычисление коэффициентов сплайнов, приближающихся к граничным точкам, как прямая линия, парабола, полином третьей степени, соответственно.

3. Задание дискретной сетки для вычисления значений сплайнов

Np := 1000 i := 0 .. Np X_i := Np

4. Вычисление значений сплайнов в узлах сетки

Y1_i := interp(vs1, x, y, X_i)

Y2_i := interp(vs2, x, y, X_i)

Y3_i := interp(vs3, x, y, X_i)

5. Визуализация сплайнов (рис. 5.6)

6. Построение разности между сплайнами различного типа в узлах координатной сетки (рис. 5.7)

7. Вычисление значений первых производных сплайнов

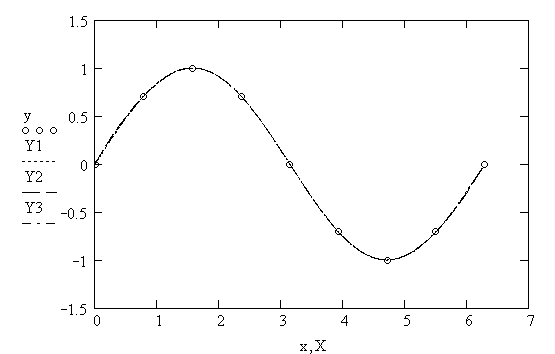
Рис. 5.6

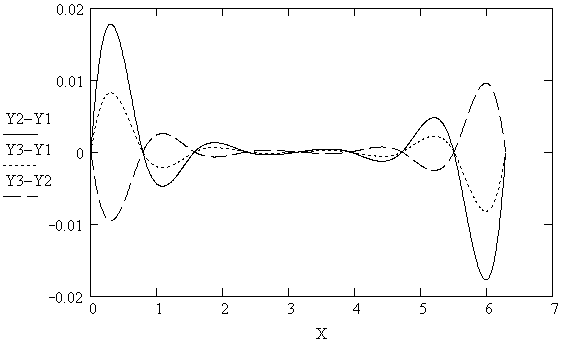
Рис. 5.7

8. Построение графиков первых производных сплайнов (рис. 5.8)

9. Вычисление значений вторых производных сплайнов

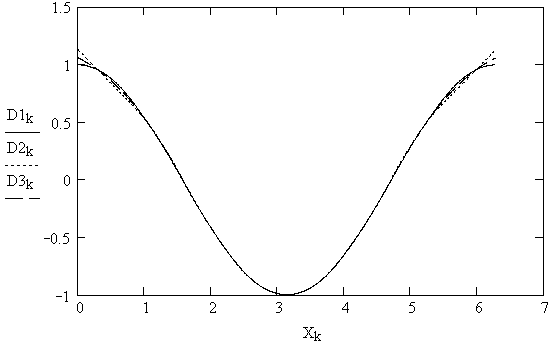
Рис. 5.8

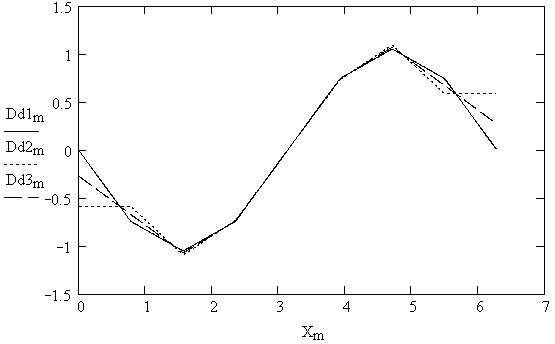
Рис. 5.9

9. Построение графиков вторых производных сплайнов (рис. 5.9)

10. Вычисление значений третьих производных сплайнов

11. Построение графиков третьих производных сплайнов (рис. 5.10)

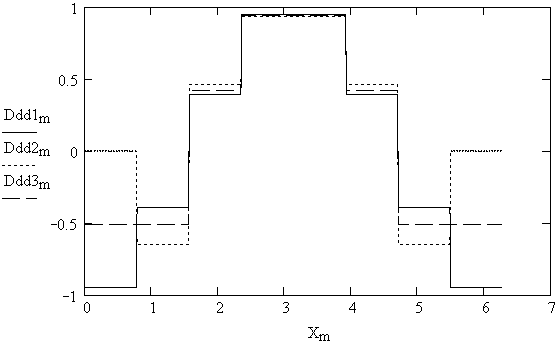
Рис. 5.10

Как видно из рис. 5.85.10, первая и вторая производные сплайнов являются непрерывными функциями, третья и производные более высокого порядкаразрывными функциями.