
книги / Физические основы нанотехнологий фотоники и оптоинформатики
..pdf
ющих эволюцией кубитов и средствами измерения состояний кубитов
(см. рис. 12.1).
Идеальный квантовый компьютер имеет состояния, которые все-
гда когерентны. Это означает отсутствие взаимодействия с окружением, создающим шумы и нарушающим когерентность вектора состояния компьютера и точное управление внешних сигналов.
Вектор состояния квантового регистра, состоящего из n кубитов, представляет собой разложение по 2n базисных состояния регистра i1, i2 , ..., in  , где i1, ..., in 0,1 .
, где i1, ..., in 0,1 .
 ai1 , i2 , ..., in i1, i2 , ..., in
ai1 , i2 , ..., in i1, i2 , ..., in  . i1 , .., in
. i1 , .., in
Здесь ai1 , ..., in – проекциивектора  нанаправленияортов i1,i2,...,in
нанаправленияортов i1,i2,...,in . Процесс вычисления на квантовом компьютере состоит в преобразовании начального вектора состояния in
. Процесс вычисления на квантовом компьютере состоит в преобразовании начального вектора состояния in компьютера в конечный
компьютера в конечный
вектор состояния f  путем умножения начального вектора на унитарную матрицу U размерности 2n 2n :
путем умножения начального вектора на унитарную матрицу U размерности 2n 2n :
f  U 2n 2n in
U 2n 2n in .
.
Вначальном состоянии компьютера все кубиты квантового регистра должны находиться в основном состоянии
in  01, 02 , ..., 0n )
01, 02 , ..., 0n ) ,
,
которое не содержит никакой информации о задаче и ее решении. Конечный вектор состояния
2n 1
f axi x x 0
содержит всю информацию о решении задачи. Измерив в базисе состояние каждого из n кубитов, в конечном состоянии получаем любое из
значений 0 x (2n 1) с вероятностями axi 2 . Квантовый алгоритм должен приводить к такому конечному состоянию f 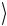 , чтобы вероятность правильного решения ps as 2 1 была близка к единице,
, чтобы вероятность правильного решения ps as 2 1 была близка к единице,
321

а сумма вероятностей всех ошибочных решений |
|
ax |
|
2 0 стреми- |
|
|
|||
x s |
|
|
||
лась к нулю.
Квантовый компьютер является цифровым вероятностным компьютером, так как дает решение задачи s с определенной вероятностью.
В квантовых вычислениях происходит преобразование начального вектора состояния в конечный вектор через непрерывный ряд состояний. Базисный набор состояний остается неизменным. Динамика состояния компьютера передается изменениями во времени амплитуд, которые являются аналоговыми величинами, принимающими непре-
рывный ряд значений в интервале 0 ax 1. По способу управления
этими величинами квантовый компьютер является аналоговым компьютером. Параметры сигналов (импульсов), управляющих кубитами, должны контролироваться с погрешностью 10–4–10–5.
Таким образом, квантовый компьютер является цифровым ве-
роятностным компьютером с аналоговым управлением, что отличает его от всех типов классических компьютеров.
Матрицу U можно разложить в упорядоченное произведение матриц второго и четвертого порядка с точностью, достаточной для вычислений:
U2n 2n Ui 2 2 U j 22 22 .
i, j
|
|
Матрица второго порядка |
|
U 2 2 |
|
|
преобразует вектор |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
в вектор |
|
|
a |
|
|
|
и описывает операцию на от- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
||||
дельном кубите i. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Матрицы четвертого порядка U 22 22 преобразуют векторы |
|||||||||||||||||||||||||||||||
состояний пар кубитов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
in a00 |
|
|
00 |
a10 |
|
10 |
a01 |
|
|
01 a11 |
|
11 |
|
f |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 . |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
a00 |
|
|
a10 |
10 a01 |
|
01 a11 |
|
|
||||||||||||||||||||
Числа сомножителей второго и четвертого порядка в разложении определяют число однокубитовых и двухкубитовых операций, необхо-
322








 , так
, так 0
0  0
0 1
1 и с окружением
и с окружением  ( 0
( 0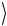 1
1 )
)  .
. и запутывается с ним:
и запутывается с ним:

 e
e

 e
e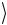

 qe
qe  e
e
 e
e
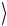








 1
1 ) в матричной форме
) в матричной форме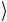 . Начальные состояния требуются также для квантовой коррекции ошибок.
. Начальные состояния требуются также для квантовой коррекции ошибок. 2 (контролирующий кубит в состоянии 0
2 (контролирующий кубит в состоянии 0 ), то при
), то при 2 (контролирующий кубит в состоянии 1
2 (контролирующий кубит в состоянии 1 ), то результатэволюции контролируемогокубита другой:
), то результатэволюции контролируемогокубита другой:  2 :
2 : 00
00 , CNOT 01
, CNOT 01 01
01 , CNOT 10
, CNOT 10 11
11 , CNOT 11
, CNOT 11 10
10 .
.