
D-M-1-Mnozh-Funkts-05r
.pdf
|
|
40 |
|
б) {1} |
{1,{1,2}}; |
д) {{1}} |
{1,{1}}. |
в) {1,2} |
{1,2{1,2}}; |
|
|
2.Задайте с помощью предикатов следующие множества:
А= {2,4,6,8,…}, B = {1,3,5,7,9,…}, C = {1,2,3,5,7,11,13,17,…}.
3.Сколько элементов содержат следующие множества:
А ={x: x Z и 5 ≤ x ≤ 10}, B = { x: x Z и x2 ≤ 36},
C ={x: x Z и 6 x2 + x – 1 = 0}, D = { x: x R и x2 + 1 = 0}.
4. Выяснить, равны ли множества А и В если:
а) A = {{1,2}, {2,3}}, |
B = {1,2,3}; |
б) A = {{1}, {2}, {3}}, |
B = {1,2,3}. |
5.Пусть А = {n: n2 – нечётное целое число}, В = {n: n – нечётное целое число}, Доказать, что А=В.
6.Ввести операции , ∩, \, . Перечислить все подмножества множества А:
а) А={1,2,3}; |
в) A={{1,2},{3},1}; |
б) A={1,{1}}; |
г) A={{1},{2},1}. |
7. Пусть А = {x: x N и 2 < x ≤ 6}, B = {x: x N и 1 < x < 4},
C = {x: x N и x2 -4 = 0}. Из каких элементов состоят множества:
A) B C; б) А∩В∩С; в) А В С?
8. |
Найдите A B, A∩B, A\B, B\A, |
A |
, |
B |
, A B , |
A |
B для: |
|
а) U={0,1,2,…,9}, A={1,2,5}, B={2,3,4,5}; |
||||||
|
б) U={0,1,2,…}, A={x: x U и x делится на 2}, B={x: x U и x |
||||||
|
делится на 3}. |
||||||
9. |
Доказать: |
||||||
а) если А (В∩С), то А В и А С;
б) если (А∩В) С то А ( B C );
в) если (А В) С то А С и В С;
г) если А (В С), то ( A ∩ B ) C .

41
10. Доказать, что для любых А1,А2,…,Аn, если А1 А2 … Аn А1, то
А1=А2=…=Аn.
11. Выяснить, выполняются ли следующие равенства:
а) А В=(А∩В) (А∩ B ) (Ā∩В);
б) А=А (А∩В);
в) A\B = А∩ B ;
г) A\(A\B) = А∩В.
12. Выяснить, выполняются ли следующие равенства:
А∩В=В∩А;
А∩(В С)=(А∩В) (А∩С);
А (В∩С)=(А В)∩(А С);
(А В)∩А=А;
А\(В\С)=(А\В) (А∩С);
А\(В С)=(А\В)\С;
А∩(В\А)= .
13. Выяснить, выполняются ли следующие равенства:
А (А В)=В; |
А (В С)=(А В) С; |
(А\B)\C=(A\C)\(B\C); |
A\(A\B)=A∩B; |
A∩(A C)=(A∩B) (A∩C). |
|
14.Пусть С = (A∩B). Постройте диаграмму Эйлера–Венна для множества С.
15.Нарисовать диаграммы Эйлера–Венна для множеств:
АB , А\(B∩C), A∩(B\C), A∩(B C).
16.Найдите 2А, если А={1,2,3}.
17.Выяснить совпадают ли множества 2А∩ 2В и 2А ∩ В если:
а) А = {a,b}, B ={b,c};
б) А и В любые непустые множества.
18. Выяснить совпадают ли множества 2А 2В и 2А В для любых непустых множеств А и В.
42
19.Доказать, что операцию \ нельзя выразить через ∩ и .
20.Решить систему уравнений:
А∩Х=В
А Х=С,
где В А С; А, В, С –данные множества, Х – искомое.
21. Решить систему уравнений:
А\Х=В
Х\А=С,
где В А, А∩С≠С; А, В, С – данные множества, Х – искомое.
22. Решить систему уравнений:
А\Х=В,
А Х=С,
где В А С; А, В, С –данные множества, Х – искомое.
23.Пусть А={а,b,с}, В={c,d}. Записать, чему равны множества A×B, В×А, А2,
В2.
24.Пусть A C, B C, А≠ , В≠ . Доказать, что A×B=(A×C)∩(C×B).
25.Доказать, что (А×В) (С×D) (A C)×(B D).
26.Выяснить, выполняются ли следующие равенства:
а) (А В)×С=(А×С) (В×С);
б) А×(В С)=(А×В) (А×С);
в) (А\В)×С=(А×С)\(В×С);
г) А×(В\С)=(А×В)\(А×С).
27. Пусть непустые множества А, В и С удовлетворяют соотношению:
А×В=А×С. Докажите, что тогда В=С.
28. Выпишите упорядоченные пары, принадлежащие следующим бинарным отношениям на множествах A={1,3,5,7} и B= {2,4,6}:
A) R= { x,y : x+y=9}; б) S={ x,y : x<y}.

43
29.Пусть R - бинарное отношение на множестве {1,2,3,4,5}, определяемое условием: nRm тогда и только тогда, когда n+m – нечётное число. Представьте R следующими способами:
а) как множество упорядоченных пар; б) в виде матрицы отношения; в) с помощью орграфа.
30.Бинарное отношение R на множестве A ={1,2,3,4} задано следующим
графом.
1 |
2 |
4 |
3 |
Перечислите упорядоченные пары, принадлежащие R, запишите матрицу отношения R.
31.Бинарное отношение R на множестве A ={1,2,3,4} задано следующим условием: xRy тогда и только тогда, когда х+2у – нечетное число. Представьте R каждым из способов:
а) как множество упорядоченных пар; б) в виде матрицы отношения; г) с помощью графа отношения.
32.Пусть R - бинарное отношение на множествах А={1,2,3} и В={1,2,3,4},
заданное перечислением пар: R={ 1,1 , 2,3 , 2,4 , 3,1 , 3,4 }. Бинарное отношение S на множествах А={1,2,3} и В={1,2,3,4}, тоже задано перечислением пар: S={ 1,1 , 1,2 , 2,1 , 3,2 , 3,4 }.
а) Задать отношения R и S с помощью матриц отношений;
б) Задать отношение R°S перечислением пар и с помощью матрицы отношения.
33. Бинарные отношения R и S заданы орграфами, представленными ниже. а) Найдите орграф для композиции этих отношений.

44
а 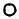
b
б) Задайте,
1 1
2 2  х
х
3 |
3 |
y |
эти отношения матрицами отношений. |
||
R |
|
S |
34. Бинарные отношения R и S заданы матрицами IR и IS соответственно, где
|
|
И |
Л |
Л |
|
|
|
|
|
И |
Л |
И |
И |
|
|
|
|
и |
|
|
= |
|
И И Л Л |
|
|
||||||
I |
R |
= |
|
|
I |
S |
|
|
. |
||||||
|
|
Л |
|
|
|
|
|
|
|
|
|
||||
|
|
И |
И |
|
|
|
|
|
Л |
И |
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
||||
Задать эти отношения орграфами. Вычислить логическое произведение этих матриц и выяснить, какому отношению оно соответствует.
35. Бинарное отношение R на множестве A= {1,2,3,4,5} задано матрицей:
|
Л |
Л |
И |
И |
Л |
|
|
|
|
|
|
|
Л |
И |
Л |
Л |
И |
L = Л |
Л |
Л |
И |
Л . |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
Л |
Л |
И |
Л |
Л |
|
|
И |
Л |
Л |
|
|
Л |
Л |
|||
Вычислить матрицу композиции R R и выяснить обладает ли R свойством транзитивности
36.Для бинарного отношения R={ x,y : x2+y2≤ 1} на множестве (-∞,∞) найти область определения и область значений.
37.Для бинарного отношения R={ x,y : y ≥ х2} на множестве (-∞,∞) найти область определения и область значений.
38.Определите, какие из приведенных ниже отношений на Z являются рефлексивными, симметричными, а какие транзитивными?
а) х+у – нечетное число; б) х+у – четное число; г) ху – нечетное число; д) х+ху – четное число.
45
39. Выяснить, какими из свойств (рефлексивность, антирефлексивность, симметричность, антисимметрчность, транзитивность) обладают следующие отношения на множестве N={1,2,3,…}:
nR1m n делитель m; nR2m n< m;
nR2m n≤ m;
nR4m n и m взаимно простые; nR5m n+m≤ 100;
nR5m n+m - четно; nR6m n+m - нечетно;
nR7m n и m имеют общий делитель отличный от 1;
nR8m n ≠ m.
40. На множестве прямых на плоскости рассмотрены отношения: а) параллельности прямых; б) перпендикулярности прямых.
Будут ли они отношениями эквивалентности?
41.На множестве людей задано отношение R: xRy тогда и только тогда, когда x и y живут в одном городе. Будет ли это отношение отношением эквивалентности?
42.Пусть N = {1,2,3,…}. На множестве N×N введено отношение R:
x,y R u,v x+v =y+u.
Выясните, будет ли R отношением эквивалентности. 43. Построить бинарное отношение:
а) рефлексивное, симметричное и нетранзитивное; б) рефлексивное, антисимметричное и нетранзитивное; в) рефлексивное, несимметричное и транзитивное;
г) нерефлексивное, антисимметричное и транзитивное.
44. Пусть на множестве {±1, ±2, ±3, …} задано отношение R следующим образом: nRm тогда и только тогда, когда m×n > 0. Является ли R отношением
46
эквивалентности? Если R отношение эквивалентности, то сколько и какие классы смежностей порождаются этим отношением?
45.Пусть R бинарное отношение, заданное на множестве городов России: хRу тогда и только тогда, когда названия городов х и у начинаются с одинаковой буквы. Является ли R отношением эквивалентности? Если R отношение эквивалентности, то каково максимально возможное число классов смежностей, на которые разбивается множество городов России?
46.Доказать, что если R1 и R2 отношения эквивалентности на А, то R1−1 , и
R1∩ R2 тоже отношения эквивалентности. 47. Для бинарных отношений доказать, что:
(R1 R2)-1=R1-1 R-12; (R1○R2)-1=R2-1○R-11.
48.Отношение R на множестве всех действительных чисел задано условием: xRy тогда и только тогда, когда х-у – целое число. Докажите, что R – отношение эквивалентности. Выпишите класс смежности, содержащий: а) элемент 0,5; б) элемент 1.
49.Пусть R бинарное отношение на множестве всех целых чисел Z = {… -3,- 2,-1,0,1,2,3,…} такое, что nRm тогда и только тогда, когда n2-m2 делится на число 3. Покажите, что R является отношением эквивалентности. Запишите: а) класс смежности, содержащий 0; б) класс смежности, содержащий 1.
50.Пусть R бинарное отношение на множестве всех целых чисел Z = {… -3,- 2,-1,0,1,2,3,…} такое, что nRm тогда и только тогда, когда n2-m2 делится на число 5. Покажите, что R является отношением эквивалентности. Сколько элементов содержит фактор-множество Z/R. Постройте все классы смежностей по отношению R.
51.Найти все отображения множества А={a,b,c} на множество В={0,1}.
52.Пусть Z – множество всех целых чисел, Z+ - множество всех неотрицательных целых чисел. Какие из следующих отношений являются функциями? Найти их области определения и значений:
а) { x,y : (x,y Z)&(y=x3)}; б) { x,y : (x,y Z+)&(x<y)};

47 |
|
в) { x,y : (x,y (-∞,∞))&(y= x )}; |
г) { x,y : (x,y Z)&(x < y≤ х+1)}; |
д) { x,y : (x,y (-∞,∞))&(x < y≤ х+1)}; |
е) { x,y : (x,y (-∞,∞))&(x = y2)}. |
53.Пусть М – множество всех жителей г. Казани. Для введённых на М
отношений Ri, 1≤ i ≤ 5, выяснить, какие из этих отношений являются функциями:
хR1у у является отцом для х;
хR2у у является сыном для х;
хR3у у является матерью для х;
хR4у у является внуком для х;
хR5у у является дедушкой для х.
54.Определите, какие из следующих отношений между множествами A={a,b,c} и B ={1,2,3} являются функциями из А в В.
а) f = {(a,1),(a,2),(b,3),(c,2)};
б) g = {(a,1),(b,2),(c,1)};
в) h = {(a,1),(c,2)}.
55.Докажите, что функция f: R→R, заданная в виде f(x)=2x+5 является биекцией.
56.Найти все отображения множества А={0,1} в А и на А и указать, какие из них инъективны, какие сюръективны и какие биективны.
57.Выясните, являются ли инъективными, сюръективными или биекциями следующие функции, заданные на множестве Z.
а) f(n)=2n+3;
б) g(n) = n / 2,
2n,
n + 1, в) h(n) =
n −1,
58. Пусть М={x: x R
если n четно
;
если n нечетно
если n четно
.
если n нечетно
и x≠2} и функция f: M→M задается формулой:
x
f (x) = . x − 2
48
Показать, что f биективная функция и найти обратную ей функцию.
59. Пусть f : А→В и g: В→С функции. Доказать, что
а) если f и g инъективны, то их композиция тоже инъективна; б) если f и g сюръективны, то их композиция тоже сюръективна.
60.Пусть f(A)={y: ( x A)&(y=f(x))}. Доказать, что функция f
удовлетворяет условию f(А∩В)= f(А)∩f(В) для любых А и В тогда и только тогда, когда функция f инъективна.
61.Пусть А и В – конечные множества, множества А и В имеют n и m
элементов соответственно ( А = n, B = m). При каких n и m существует инъективное отображение А в В?
62. Какие функции на (-∞,∞), из заданных далее, инъективны, сюръективны, биективны:
y=2x, y=x3, y=x2+1, y=x+1?
63.Равномощны ли множество точек окружностей радиуса 1 и 10?
64.Равномощны ли множество точек отрезка [0,1] и [-10,10]?
65.Равномощны ли множество точек единичного квадрата и единичного отрезка?
66.Равномощны ли множество всех натуральных чисел и множество неотрицательных четных натуральных чисел?
67.Используя характеристические функции множеств, выясните, выполняются ли следующие равенства:
а) ( A B) ∩ C = ( A ∩ C) (B ∩ C) ;
б) ( A B) C = A (B C) ;
в) А\ (В \ С) =(А \ B) \ C;
г) A ∩ (B C) = ( A ∩ B) ( A ∩ C) .
68. Пусть R отношение частичного порядка на множестве А. Образует ли R -1 частичный порядок на А?
69. Какие из следующих множеств чисел, упорядоченных по величине, будут вполне упорядочены:
49
1)множество всех целых чисел;
2)множество всех целых положительных чисел;
3)множество всех целых отрицательных чисел;
4)множество всех рациональных чисел;
5)множество всех чисел вида (2/3)n, n=1,2,3,…;
6)множество всех чисел вида (3/2)n, n=1,2,3,…;
7)множество всех чисел вида 1/n, n=1,2,3,….
70.На множестве N×N, N={1, 2, 3,…} введено отношение R: а,b R c,d
тогда и только тогда, когда a≤ c и b≤ d. Будет ли N×N при этом частично упорядоченным или линейно упорядоченным?
