
D-M-1-Mnozh-Funkts-05r
.pdf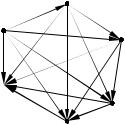
20
5) отношение R на конечных множествах А и В можно задать n m (логической) матрицей отношения вида LR =(lij), здесь n и m числа элементов в множествах А и В соответственно и
И, если аi ,b j R, ai A, b j B, lij = Л, если аi ,b j R, ai A, b j B.
6)бинарное отношение R на конечном множестве А можно задать графом. Пусть A={a1, a2, …, an}, тогда элементы ai (1≤ i ≤ n)
рассматриваются как вершины графа. Если ai,аj R, то из вершины ai идёт дуга в вершину aj, иначе – из ai нет дуги в aj. В результате получим орграф, представляющий отношение R. Ясно, что бинарное отношение R на конечных множествах А и В тоже можно задать графом, выбирая в качестве вершин элементы из А В. При этом если ai,bj R, то из вершины ai идёт дуга в вершину bj, иначе – из ai
нет дуги в bj.
Пусть, например, А = {1, 2, 3, 4, 5, 6} и R таково, что: aRb тогда и только тогда, когда a < b. Рассмотрим некоторые способы задания этого отношения.
Задание R перечислением: R={ 1,2 , 1,3 , …, 1,6 , 2,3 , 2,4 ,…, 2,6 ,
…, 5,6 }. |
|
|
|
|
|
|
|
|
|
|
|
Задание R матрицей АR: |
|
|
Задание R орграфом дано на Рис. 1.9. |
||||||||
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
0 |
0 |
1 |
1 |
1 |
1 |
3 |
|||
|
|
||||||||||
|
= 3 |
|
0 |
0 0 1 1 |
1 |
|
|
|
|||
AR |
|
|
6 |
|
|||||||
|
4 |
|
0 |
0 |
0 |
0 |
1 |
1 |
|
|
|
|
5 |
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
4 |
|
|
|
|
|
|||||||
|
6 |
|
|
0 |
0 |
0 |
0 |
|
|
|
5 |
|
0 |
0 |
|
|
|||||||
Рис. 1.9
21
Матрица LR =(lij) отношения R получится из матрицы АR , если в этой матрице всюду вместо 1 записать И, а вместо 0 записать Л. В результате получим:
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
Л |
И |
И |
И |
И |
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Л |
Л |
И |
И |
И |
И |
|
|
|
3 |
|
Л |
Л |
Л |
И |
И |
И |
LR |
= |
4 |
|
|
Л |
Л |
Л |
И |
|
|
|
Л |
И |
||||||
|
|
5 |
|
Л |
Л |
Л |
Л |
Л |
|
|
|
|
И |
||||||
|
|
6 |
|
|
Л |
Л |
Л |
Л |
|
|
|
Л |
Л |
||||||
§ 5. Операции над отношениями
Так как отношения на А и В являются подмножествами, то над ними можно ввести все теоретико-множественные операции, например:
1)пересечение отношений (R1∩R2), здесь и далее в перечисляемых пунктах 2)-4), R1 и R2 произвольные бинарные отношения;
2)объединение отношений (R1 R2);
3)разность отношений (R1\R2);
4)дополнение к данному отношению R: СR = R = (A B)\R, x,y R
тогда и только тогда, когда x,y R.
Кроме того, введем новые операции: |
|
||
5) обратное к R отношение R-1={ b,a : а,b R}. |
|
||
В дальнейшем вместо слов |
«тогда и только тогда» |
||
|
|||
записываем: ; |
|
|
|
||
вместо «существует» записываем: ; |
||
|
||
вместо «всех (каждого)» записываем: . |
|
22
6) композиция отношений. Пусть R – отношение на множествах А и В, S – отношение на множествах В и С. Тогда композицией R и S называется отношение (обозначаемое R°S) на множествах А и С такое, что:
a,c (R°S) b(b B и a,b R и b,c S).
Если R определено на А, В, а S на C, D, В∩С= , то R°S не определено.
Свойства операций над отношениями. Для пересечения,
объединения и дополнения отношений справедливы все свойства, установленные ранее (см. равенства 1)-19) в теореме 1.1). Кроме того, можно доказать следующие свойства:
1)R1°(R2°R3)=(R1°R2)°R3 – ассоциативность композиции;
2)(R1°R2)-1=R2-1°R1-1;
3)С(R-1)=(СR)-1;
4)(R1 R2)-1=R1-1 R2-1;
5)(R1∩R2)-1=R1-1∩R2-1;
6)R1°(R2 R3)=(R1°R2) (R1°R3);
7)если R1 R2, то R1-1 R2-1.
Свойства отношений на множестве A. Бинарное отношение R на
множестве А называется:
1)рефлекcивным, если для а А а,а R;
2)антирефлексивным (иррефлексивным), если для а А а,а R;
3)симметричным, если из x,y R следует, что y,x R;
4)антисимметричным, если из x,y R и y,x R следует, что х=у;
5)транзитивным, если из x,y R и y,z R следует, что x,z R.
Можно ввести и другие свойства, которыми могу обладать или не обладать бинарные отношения на множестве А. Отметим следующее. Бинарное отношение, которое не является рефлексивны не обязательно является антирефлексивным (иррефлексивным). Могут быть отношения,

23
которые не обладают свойствами, как рефлексивности, так и антирефлексивности. Приведем пример. На множестве точек плоскости с прямой L введем отношение R: а,b R тогда и только тогда когда точки а и b симметричны относительно прямой L (а и b лежат на одном перпендикуляре к L и на одинаковом расстоянии от L в разных замкнутых полуплоскостях определяемых прямой L). Для любой точки а лежащей на L имеет место
а,а R, а для точки не лежащей на L, имеем: а,а R. Таким образом, это отношение не обладают свойствами, как рефлексивности, так и антирефлексивности. Из этого следует: если отношение не является рефлексивным, то это не означает, что оно антирефлексивно.
Построим пример отношения, которое не обладает свойствами, например, симметричности и антисимметричности. Пусть задано трехэлементное множество М = {1,2,3} и отношение R задано матрицей отношения:
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
AR |
= 0 |
1 |
1 |
. |
|
|
|
1 |
0 |
0 |
|
|
|
|
|||
Это отношение не является симметричным: из того, что 1,2 R не следует,
что 2,1 R. Также это отношение не является антисимметричным: из того,
что 1,3 R и 3,1 R не следует, что 1=3. Таким образом, каждое из свойств
1)-4) нужно устанавливать отдельно.
Теорема 1.2. Пусть R – бинарное отношение на А. Тогда:
1)R рефлексивно E R;
2)R антирефлексивно R∩Е= ;
3)R симметрично R=R-1;
4)R антисимметрично R∩R-1=E;
5)R транзитивно R°R=R.

24
Доказательство: Рассмотрим утверждение 1). Необходимость условия:
если R рефлексивно, то для a A имеет место a,a R, отсюда следует, что
E R. Достаточность условия: пусть E R, тогда для a A имеем a,a R, а это и означает, что R рефлексивно.
Рассмотрим утверждение 2). Необходимость докажем от противного.
Пусть R∩Е≠, тогда найдется а А, что a,a R и a,a Е, но этого не может быть, ибо для а А имеем а,а R. Итак, R∩Е= . Достаточность. Пусть
R∩Е= . Это означает, что не существует а А, что a,a R и a,a Е. Тогда для любого а А выполняется а,а R, что и требовалось.
Аналогично доказываются утверждения 3) - 5).
Теорема 1.3. Если бинарное отношение R на множестве А обладает любым из указанных свойств 1)-5), то обратное отношение R-1 обладает этим же свойством.
Доказательство. 1) Если E R, то E-1 R-1, но Е-1=Е, следовательно,
E R-1, т.е. R-1 рефлексивно;
2) если R∩Е= , то (R∩Е)-1 , тогда (R-1∩Е) , следовательно,
(R-1∩Е) = ;
3) очевидно, что (R-1)-1=R, а по условию R=R-1, следовательно, (R-1)-1 = R-1, т.е. R-1 симметрично.
Аналогично доказываются утверждения 4), 5).
§ 6. Функция
Определим функцию, следуя Дирихле. При таком определении отождествляется функция с ее графиком. Существуют другие определения, когда функция рассматривается как правило (алгоритм) вычисления; такие
25
определения будут вводиться в курсе математической логики и теории алгоритмов.
Бинарное отношение f на множествах А и В называется функцией, если образ каждого элемента (при этом отношении) единственен, т.е. из x,y f и
x,z f следует, что y=z.
Пусть отношение f является функцией (f A B). Область определения
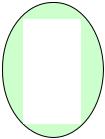
Df функции f является подмножеством множества А (Df А), а область значений Imf является подмножеством множества В (Imf B). Если Df является собственным подмножеством множества А, то говорят, что задана частично определенная функция. Если область определения совпадает с А, то говорят, что задана всюду определенная функция или задана функция. На рис. 1.10 изображены области определения и области значений различных функций и частично определённых функций.
Функцию f (с областью определения Df и с областью значения Imf, Imf
В) иногда называют отображением множества А в множество В; если же область значений функции совпадает с В, то f называют отображением множества А на множество В.
A |
B |
A |
B |
|
f |
|
f |
Df =A |
Imf B или |
Df A |
Imf B или |
|
Imf =B |
|
Imf =B |
|
для функции |
для частично определенной функции |
|
Рис. 1.10
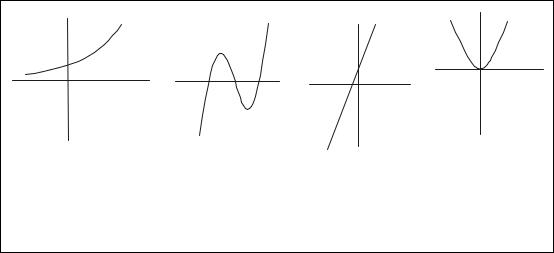
|
|
26 |
|
|
Для функции вместо x,y f или xfy записывают y=f(x) или f: A→B. |
||||
Если y=f(x), то х называют аргументом, а у – значением функции f. |
|
|||
Функция f называется инъективной, если для x1,x2 из f(x1)=f(x2) |
||||
следует, что x1=x2 (иными словами из x1≠ x2 следует, что f(x1)≠ f(x2)). |
|
|||
Функция f (f: A→B) называется сюръективной, если для любого у В |
||||
существует х А такой, что y=f(x). Иными словами функция будет |
||||
сюръективной если область значений функции f: A→B совпадает со всем |
||||
множеством В. |
|
|
|
|
Функция f (f: A→B) называется биективной (биекцией), если f |
||||
инъективна и сюръективна. Следовательно, f биективна, если она |
||||
осуществляет взаимно однозначное отображение (соответствие) между |
||||
множествами А и В. |
|
|
|
|
Рассмотрим пример. Пусть А=(-∞,∞), fi: A→A |
(i=1,2,3,4) и f1(x)=ex, |
|||
f2(x)=x3-x, f3(x)=2x+1, |
f4(x)=x2. Их графики представлены на рис. 1.11. Легко |
|||
выяснить, когда эти функции инъективны, сюръективны или биективны. |
|
|||
y=e |
x |
3 |
|
2 |
|
y=x -x |
y=x |
||
|
|
|||
|
|
y=2x+1 |
|
|
|
|
|
|
|
инъективна, но |
не инъективна, |
не инъективна и |
||
не сюръективна |
||||
не сюръективна |
но сюръективна биективна |
|
|
|
|
|
Рис. 1.11 |
|
|
Можно доказать следующие теоремы. |
|
|
||
27
Теорема 1.4. Функция f имеет обратную функцию f -1 тогда и только тогда, когда f биективна.
Теорема 1.5. Композиция биективных функций является функцией биективной.
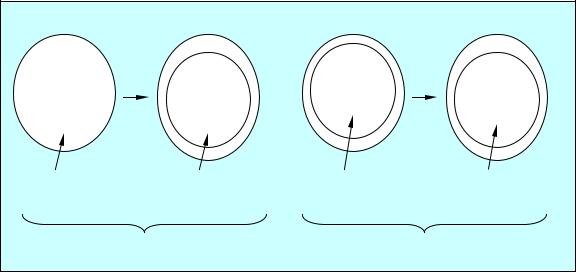
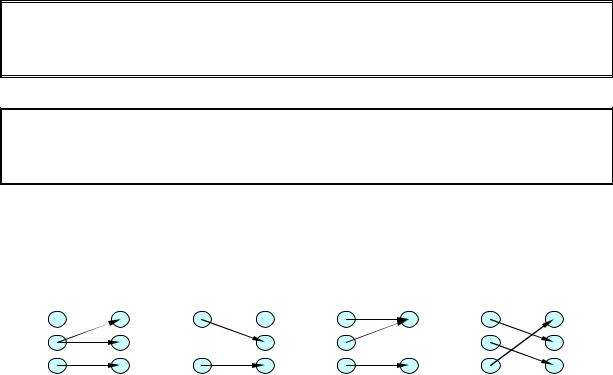
Рис. 1.12 показывают различные отношения, все они, кроме первой, являются функциями.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отношение, но |
инъекция, но |
сюръекция, но |
биекция |
|
|||||||||||
|
не функция |
не сюръекция |
не инъекция |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.12 |
|
|
|
|
|||||
Пусть f : А→В – функция, а множества А и В - конечные множества,
положим А = n, B = m. Принцип Дирихле гласит, что если n > m, то, по крайней мере, одно значение f встречается более одного раза. Иными словами, найдется пара элементов ai ≠ aj, ai, aj A, для которых f(ai)= f(aj).
Принцип Дирихле легко доказать, поэтому оставляем его читателю в качестве тривиального упражнения. Рассмотрим пример. Пусть в группе более 12 студентов. Тогда, очевидно, что, по крайней мере, у двоих из них день рождения в одном и том же месяце.
28
§ 7. Характеристическая функция множества
Пусть задано множество U и его подмножество А. Характеристической функцией подмножества А считают функцию:
A |
1, |
если |
x A |
(x) = |
если |
x U. |
|
|
0, |
x A, |
|
Множества А и В |
равны |
тогда |
и только тогда, когда для |
x, x U : A ( x) = B ( x) . Легко видеть, что:
[ A ( x)]2 = A ( x).
Очевидно, что характеристическая функция для дополнения множества А будет равна:
|
|
|
|
|
. |
|
|
0, |
если |
x A |
(1.1) |
|
|
(x) = |
|
|
= 1 - A ( x) |
A |
если |
x A |
|||
|
|
1, |
|
Построим характеристическую функцию для пересечения и объединения множеств. Характеристическая функция для пересечения должна принимать значение 1 для тех элементов х из U, которые принадлежат множествам А и В одновременно, и значение 0 в противном случае. Легко видеть, что этому требованию удовлетворяет функция:
A∩B (x) = A (x) B (x). |
(1.2) |
Можно получить, что для объединения множеств А и В имеем: |
|
A B (x) = A ( x) + B (x) - A ( x) B ( x). |
(1.3) |
Для разности и симметрической разности можно получить |
|
соответственно: |
|
A\ B (x) = A ( x) - A (x) B ( x), |
(1.4) |
A B ( x) = A (x) + B (x) - 2 A ( x) B ( x). |
(1.5) |
29
Используя характеристические функции можно выяснять, равны или нет те или иные множества. Покажем это на примерах. Докажем соотношение:
A\(A\B) = A∩B. |
(1.6) |
Для этого найдем характеристические функции для множества стоящего в левой части соотношения (1.6). Последовательно имеем:
µA\ ( A\ B) ( x) = µ A ( x) - µ A ( x)µ A\ B ( x) =
=µ A ( x) - µ A ( x)(µ A ( x) - µ A ( x)µB ( x)) = µ A ( x)µB ( x).
Получили, что характеристическая функция левой части для (1.6) равна
µ A ( x)µB ( x) , а эта характеристическая функция для A∩B, следовательно,
множества тоже совпадают.
Приведем таким способом доказательство соотношения 7 из теоремы 1.1, т.е. нужно выяснить имеет ли место равенство:
A (B∩C)=(A B)∩(A C). |
(1.7) |
Выясним чему равны характеристические функции для множеств стоящих в левой и правой частях соотношения (1.7). Для множества стоящего в левой части имеем:
µ A ( B ∩C ) ( x) = µ A ( x) + µB ∩C ( x) - µ A ( x) µB ∩C ( x) = = µ A ( x) + µB ( x) µC (x) - µ A ( x) µB ( x) µC (x).
Для множества стоящего в правой части (1.7) получим:
µ( A B)∩( A C ) ( x) = µ A B ( x) µ A C ( x) =
=( A ( x) + B ( x) - A ( x) B (x))( A ( x) + C ( x) - A ( x) C (x)) =
=µ A ( x) + µ A ( x)µC ( x) - µ A ( x)µC (x) + µ A ( x)µB (x) + µB ( x)µC (x) -
−µ A ( x) µB ( x)µC ( x) - µ A ( x)µB ( x) − µ A ( x) µB ( x)µC ( x) + µ A ( x) µB ( x)µC ( x) =
=µ A ( x) + µB ( x) µC (x) - µ A ( x) µB ( x) µC (x).
Таким образом, левые и правые части соотношения (1.7) имеют одинаковые характеристические функции, следовательно, множества стоящие в левой и правой частях (1.7) равны.
