
лекцииматан Copy
.pdf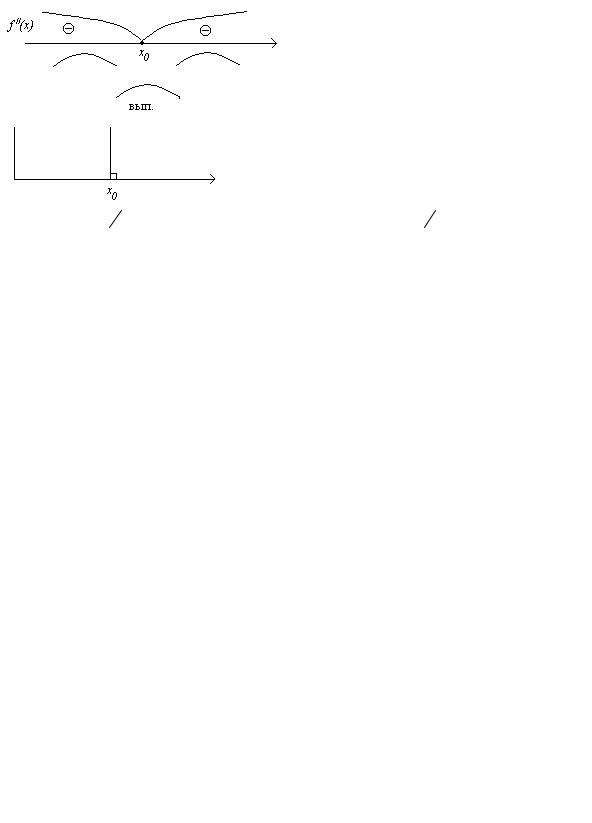
f ′( x |
) |
f ′′( x |
) |
0 |
|
0 |
|
Первый достаточный признак существования у функции точки перегиба. Пусть функция y = f ( x) дифференцируема в точке х0 или имеет в этой
точке бесконечную производную.
Тогда если функция y = f ( x) дважды дифференцируема в окрестности
точки х0 за исключением, быть может, ее самой, и при переходе через х0 вторая производная функции меняет знак, то х0 является точкой перегиба. Причем если переход осуществляется с «+» на «–», то перегиб будет от вогнутости к выпуклости, а если с «–» на «+», то от выпуклости к вогнутости.
Если вторая производная не меняет знака при переходе через точку х0, то х0 не является точкой перегиба.
Доказательство:
Доказательство следует из критерия выпуклости (вогнутости) для дважды дифференцированной функции и из непрерывности функции в точке
х0.
Второй достаточный признак существования у функции точки перегиба в терминах высших производных.
71

|
|
Пусть х0 стационарная точка функции y = f ( x) по второй производной |
||||||||||||||||||||||||||||
и в окрестности точки х0 функция |
f ( x) имеет производные до n-ого порядка |
|||||||||||||||||||||||||||||
включительно, |
причем f ¢¢( x |
|
) = |
f ¢¢¢( x |
) = ... = f (n−1) |
( x |
) = 0 , |
а |
f (n) ( x |
|
) ¹ 0 , |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
0 |
|
|
||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
если n |
– |
|
|
нечетное, |
то |
|
х0 |
является точкой |
перегиба, причем |
|
если |
|||||||||||||||||
|
|
f (n) ( x |
) < 0 , то перегиб осуществляется от вогнутости к выпуклости |
|
||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если f |
(n) ( x ) > 0 , то от выпуклости к вогнутости |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
n – |
четное, то х0 не является точкой перегиба. |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство: |
|
|
|
|
|
|
|
|||||||
|
|
Разложим |
|
функцию |
y = f ′′( x) по формуле |
Тейлора |
в |
окрестности |
||||||||||||||||||||||
точки х0. |
|
|
|
|
|
f ¢¢¢( x |
) |
|
|
|
|
|
|
f (4) ( x |
) |
|
|
f (n−2) ( x ) |
|
|
|
|
||||||||
|
¢¢( x |
) = f ¢¢( x |
) + |
|
( x |
- x |
) + |
|
( x - x ) + ... + |
( x - x ) |
n−4 |
+ |
||||||||||||||||||
f |
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(n - 4)! |
|
|
||||||||||||||||||
|
0 |
|
|
|
0 |
|
|
|
1! |
|
|
|
|
0 |
|
|
|
2! |
|
0 |
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ |
f (n−1) ( x |
) |
( x |
- x ) |
n−3 |
+ |
|
f (n) ( x ) |
( x - x ) |
n−2 |
+ R ( x). |
|
|
|
|
|
|
|
||||||||||||
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||
(n |
- 3)! |
|
|
(n - 2)! |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f ¢¢( x) = |
f |
(n) ( x ) |
( x - x ) |
n−2 |
+ R ( x). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(n - 2)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x - x0 ) < 0 |
( x - x0 ) > 0 |
n – нечетное (n–2) – нечетное
( x - x0 )n−2
1) f (n) ( x0 ) < 0
f |
(n) ( x |
) |
( x - x |
) |
n−2 |
> 0 |
f |
(n) ( x |
) |
( x - x |
) |
n−2 |
< 0 . |
|
0 |
|
|
|
0 |
|
|
||||||
(n - 2)! |
|
(n - 2)! |
|
||||||||||
0 |
|
|
|
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Согласно первому достаточному признаку существования у функции точки перегиба. так как вторая производная при переходе через точку х0 меняет знак с «+» на «–« имеем: х0 является точкой перегиба, причем перегиб осуществляется от вогнутости к выпуклости.
f (n) ( x0 ) > 0
f |
(n) ( x |
) |
( x - x ) |
n−2 |
f |
(n) ( x |
) |
( x - x ) |
n−2 |
|
0 |
|
|
|
0 |
|
|
||
(n - 2)! |
|
(n - 2)! |
|
||||||
0 |
|
0 |
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
72 |
|

если n – |
четное |
|
|
|
||||
(n–2) – |
четное |
|
|
|
||||
f ′′( x) = |
f (n) ( x |
) |
( x − x0 ) |
n−2 |
+ R ( x). |
|||
|
|
|
0 |
|
|
|||
(n |
− 2)! |
|
||||||
|
|
|
|
|||||
если f (n) ( x |
|
|
) > 0 f ′′( x) > 0 |
|||||
|
0 |
|
|
|
|
|
||
f (n) ( x |
|
) < 0 f ′′( x) < 0 . |
||||||
|
0 |
|
|
|
|
|
|
|
В силу первого достаточного признака, т.к. вторая производная не меняет знака при переходе через точку х0, то х0 не является точкой перегиба.
АССИМПТОТЫ К ГРАФИКУ ФУНКЦИИ.
Прямая называется асимптотой кривой, если расстояние от точки кривой до асимптоты стремится к нулю при неограниченном удалении этой точки по кривой от начала координат.
Асимптотой кривой называется такая прямая, к которой неограниченно приближается точка кривой при неограниченном удалении ее от начала координат.
вертикальные x = a
lim f ( x) = ∞
x→a
Прямая x = a называется вертикальной асимптотой к графику функции y = f ( x), если хотя
бы один из пределов
Асимптоты.
горизонтальные y = b
lim f ( x) = b
x→∞
Прямая y = b называется горизонтальной асимптотой к графику функции y = f ( x),
если при x → ∞ предельное значение функции равно b.
73
наклонные y = kx + b
k = lim |
|
|
f ( x) |
|
|||||
|
|
|
x |
|
|
|
|||
x→∞ |
( |
|
|
|
) |
||||
x→∞ |
( |
f |
x |
) |
− kx |
||||
b = lim |
|
|
|
|
|
||||
Прямая |
|
|
|
|
y = kx + b |
||||
называется наклонной асимптотой к графику
функции |
y = f ( x), |
если |
предел |
lim f ( x) − (kx + b) = 0 |
|
x→∞ |
|

при x → a |
(правый |
|
|
|
|
|
причем если x → +∞ , |
|
или |
левый) |
|
|
|
|
|
то прямая |
называется |
обращается |
в |
|
|
|
|
|
правой |
наклонной |
бесконечности. |
|
|
|
|
|
асимптотой; |
если |
|
|
|
|
|
|
|
|
x → −∞ , то левой. |
|
Замечание: |
Если предел lim |
f ( x) |
= lim |
f ( x) |
= k , то левая |
и правая |
||
x |
|
|||||||
|
|
x→+∞ |
x→−∞ |
x |
|
|||
наклонная асимптоты совпадают.
Если k = 0 , то наклонная асимптота совпадает с горизонтальной.
Общая схема исследования и построения ее графика. 1. Найти область определения функции
g ( x) > 0
( ) = ( ) ( ) ¹
F x log f ( x) g x f x 1
f ( x) > 0
F ( x) = |
1 |
g ( x) ¹ 0 |
|
g ( x) |
|||
|
|
F ( x) 2n g ( x) g ( x) ³ 0 .
2. Найти точки разрыва и определить их характер.
Разрыв первого рода (скачок, устранимый) разрыв второго рода. Вычислить пределы слева и справа в точках, подозрительных на
разрыв.
3. Исследовать функцию на четность и нечетность
f (-x) = f ( x) - четная (симметрия относительно оси ОУ)
f (-x) = - f ( x) - нечетная (симметрия относительно начала координат).
4. Найти точки пересечения с осями координат
Iox : y = 0 0 = f ( x) ( x0 ,0)
Ioy : x = 0 y0 = f ( x) (0, y0 ) .
5. Найти промежутки знакопостоянства y > 0 f ( x) > 0 x Î(...)
y < 0
6. Найти промежутки возрастания и убывания, а также точки экстремумов, если они есть.
Необ. f ′( x) = 0 $f ′( x) x0 критическая точка. Первый достаточный признак f ′( x)
74

Второй достаточный признак.
f |
′( x |
) = 0 |
|
|
|
|
|
0 |
|
|
|
|
|
f |
¢( x |
) = f |
¢¢( x |
) = ... = f |
(n) ( x |
) ¹ 0 |
|
0 |
|
0 |
|
n |
|
f |
(n+1) ( x ) = 0 |
1) n – |
четн. ®extr |
|||
|
|
0 |
|
|
|
|
2)n – нечет. ® extr нет.
7.Найдем промежутки выпуклости и вогнутости функции и точки перегиба,
если они есть.
Необ.
|
′′( x |
) = 0 |
|
Второй достаточный признак |
|||
f |
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
f |
¢¢( x |
) |
= f ¢¢¢( x |
) = ... = f (n−1) ( x ) = 0 |
|
|
|
|
0 |
|
0 |
|
n |
|
|
f (n) ( x |
) ¹ 0 |
1) n – |
четн. перегиба нет |
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
2) n – |
нечетн. перегиб есть. |
|
|
8. Найти асимптоты к графику функции |
|
||||||
|
1) |
вертикальные x = a lim f ( x) = ∞ т.р. второго рода. |
|||||
|
|
|
|
|
x→a |
|
|
|
2) |
горизонтальные y = b lim f ( x) = b - const, асимт. есть |
|||||
|
|
|
|
|
x→∞ |
¥, |
асимпт. нет |
75

|
|
f ( x) |
k, накл. асимпт. есть |
|
|
|
|
3) наклонные |
y = kx + b lim |
|
= ∞, нет |
|
|||
|
x→∞ |
x |
|
|
|
||
|
|
|
0, накл совпадает с горизон. |
9. Построить график функции, используя результаты предыдущих шагов.
Пример: y = |
|
2x3 |
. |
|
||||||
x2 − 4 |
|
|||||||||
|
|
|
|
|
|
|
|
|
||
1) D ( f ) : (−∞; −2) U (−2;2) U (2; +∞) . |
||||||||||
2) x0 = 2 |
|
|
x0 = −2 |
|
||||||
lim |
|
2x3 |
= |
−16 |
|
= −∞ |
||||
|
|
|
|
|
|
|||||
|
|
2 |
− 4 |
|||||||
x→−2−0 x |
|
|
|
|
+0 |
|
|
|||
lim |
2x3 |
|
= |
−16 |
|
= +∞ |
||||
|
|
|
|
|
|
|||||
|
2 |
− 4 |
|
|||||||
x→−2+0 x |
|
|
|
|
0 |
|
|
|||
lim |
2x3 |
|
= −∞ |
lim |
2x3 |
|
= ∞ . |
||
|
− |
4 |
|
− |
4 |
||||
x→2−0 x2 |
|
x→2+0 x2 |
|
||||||
3) f (−x) = |
2(−x3 ) |
= |
−2x3 |
= − f ( x) |
|
|
|||
|
(−x)2 − 4 x2 − 4 |
|
||
симметрична относительно начала координат.
4) |
Iox : y = 0 0 = |
|
2x3 |
|
|
x = 0 (0;0) |
|||||
|
x2 − |
4 |
|||||||||
|
|
|
|
|
|
|
|
|
|||
Ioy : x = 0 y = |
0 |
= 0 |
(0;0) |
|
|||||||
−4 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
2x3 |
|
|
|
2x3 |
|||||
5) |
y > 0 |
|
> 0 |
|
|
|
> 0 |
||||
x2 − 4 |
|
|
( x − 2)( x + 2) |
||||||||
76

|
6x |
|
( x |
|
- 4) - 2x |
|
× 2x |
|
|
|
|
|
|
|
|
|
2x |
2 |
(x - |
|
)(x + |
|
) |
||
|
2 |
2 |
3 |
|
6x |
4 |
- 24x |
2 |
- 4x |
4 |
|
12 |
12 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
6) y¢ = |
|
|
|
|
|
|
|
= |
= |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
(x2 - 4)2 |
|
|
|
|
(x2 - 4)2 |
|
|
|
( x - 2)2 ( x + 2)2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Критические точки f ′( x) = 0 ; x = 0 x = |
|
|
|
x = - |
|
|
|||||||||||||||||||
12 |
|
12 |
|||||||||||||||||||||||
|
|
|
|
|
$f ′( x) ; x = 2 x = −2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y (-2 |
|
) = -6 |
|
y (2 |
|
) = 6 |
|
|
3 |
3 |
3 |
3 |
|
|
2x |
4 |
- 24x |
2 |
|
¢ |
|
16x (x |
2 |
+12) |
|
16(x |
2 |
+12) |
|
|
7) y¢¢ = |
|
|
|
|
= |
|
= |
|
/ |
||||||||
(x2 - 4)2 |
|
|
|
(x2 - 4)3 |
( x - 2)3 ( x + 2)3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
Критические точки |
|
|
|
|
|
|
|
|
|
|
|||||||
f ′′( x |
) = 0 |
|
x = 0 |
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$f ′( x |
) ; x = 2 x = −2 . |
0 |
|
8) Асимптоты вер. x = 2 x = −2
гор. lim |
2x3 |
|
= ¥ нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x→∞ x2 - |
|
|
f ( x) |
|
|
|
|
|
|
|
|
|
|||||
накл. y = kx + b k = lim |
= lim |
|
2x3 |
|
= lim |
2x3 |
|||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
x→∞ |
|
|
x |
|
|
x→∞ |
(x2 - 4) x x→∞ x2 - 4 |
|||||||
b = lim ( |
f ( x) - kx) = lim |
|
2x3 |
|
|
|
2x3 - 2x3 + 8x |
||||||||||
|
|
|
|
|
- 2x |
= lim |
|
|
|
|
|
||||||
|
2 |
- 4 |
|
x |
2 |
- 4 |
|||||||||||
|
|
|
|
x |
|
|
|
x→∞ |
|
|
|||||||
y = 2x .
= 2 |
|
|
= lim |
8x |
= 0 |
|
||
x→∞ x2 - 4 |
||
77
