
лекцииматан Copy
.pdf
Число А называется правым пределом функции y = f ( x) в точке х0,
если
"ε > 0 $δ (ε ) > 0 x Î( x0 , x0 + δ (ε )) f ( x) - A < ε .
Точка х0 называется точкой разрыва первого рода, если в ней нарушается условие непрерывности
lim |
f ( x) = lim |
f ( x) = lim f ( x) = f ( x0 ) |
x→x0 −0 |
x→x0 +0 |
x→x0 |
и пределы слева и справа у функции в этой точке конечны.
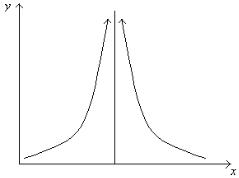
Точка х0 называется точкой разрыва второго рода, если хотя бы один левый или правый предел обращается в бесконечность.
Классификация точек разрыва первого рода.
Точка разрыва первого рода называется точкой устранимого разрыва, если предел справа равен пределу слева.
Точка разрыва первого рода называется точкой скачка, если предел справа в этой точке не равен значению пределу слева в этой точке, т.е.
lim f ( x) = A |
|
lim f ( x) = B A ¹ B, A, B = const . |
|||
x→x0 |
−0 |
|
x→x0 +0 |
||
|
Величина |
|
A - B |
|
называется величиной скачка. |
|
|
|
|||
Геометрическая иллюстрация точек разрыва.
31
Основные элементарные функции.
Под основными элементарными функциями понимают функции следующего вида:
1) y = f ( x), f ( x) = c, c = const постоянная
2)f ( x) = xα - степенная функция
3)f ( x) = ax - показательная
4)f ( x) = loga x
|
sin x |
|
|
|
|
|
cos x |
|
5) |
f ( x) = |
|
|
tgx |
|
|
|
|
|
ctgx |
|
|
arcsin x |
|
|
|
|
6) |
arccos x |
обратные тригонометрические функции |
f ( x) = |
||
|
arctgx |
|
|
|
|
|
arcctgx |
|
f ( x) = |
sin2 |
x |
+ arctgx . |
x3 |
|
||
|
|
|
|
Определение: функция, образованная из однообразных элементарных |
|||
функций при помощи операций сложения, вычитания, умножения, деления и возведения в степень, называется элементарной функцией.
Теорема:
Все основные элементарные функции непрерывны в своей области
определения. |
|
|
|
π |
π |
|
Дано: f ( x) = tgx |
X = |
|
- |
|
||
|
|
; |
. |
|||
|
|
|
|
2 |
2 |
|
Доказать: f ( x) непрер. |
x X . |
|||||
Определение № 2. |
lim |
|
y = |
0 . |
|
|
|
x→0 |
|
|
|
|
|
Доказательство: Dy = f ( x0 + Dx) - f ( x0 ) приращение функции
Dy = tg ( x0 + Dx) - tgx0 |
= |
sin ( x0 + Dx - x0 ) |
= |
|
sin Dx |
||
cos( x0 |
+ Dx)cos x0 |
cos( x0 |
+ Dx) × cos x0 |
||||
|
|
|
|||||
|
|
|
32 |
|
|
|
|
|
|
sin |
x |
|
sin 0 |
|
0 |
|
|
|
|
π |
π |
||
lim |
y = lim |
|
|
|
= |
|
|
= |
|
|
x0 |
= |
− |
; |
. |
x→0 |
x→0 cos( x0 |
+ |
x)cos x0 |
|
cos |
x0 |
|
cos |
x0 |
|
|
|
2 |
2 |
|
Следствие: все элементарные функции непрерывны в своей области определения.
Предел функции в бесконечности.
lim f ( x) = A .
x→∞
Число А называется пределом функции в бесконечности, если
ε > 0 δ (ε ) > 0 x > δ (ε ) f ( x) − A < ε .
lim f ( x) = A : ε > 0 |
δ (ε ) > 0 |
x > δ (ε ) |
|
f ( x) − A |
|
|
< ε |
|||||||||||
|
|
|||||||||||||||||
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ (ε ) > 0 |
x > −δ (ε ) |
|
f ( x) − A |
|
|
|
|
|||||||||||
lim f ( x) = A : ε > 0 |
|
|
< ε . |
|||||||||||||||
|
|
|||||||||||||||||
x→−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Бесконечный предел функции в точке. |
||||||||||||||||||
lim f ( x) = ∞ ε > 0 |
δ (ε ) > 0 |
0 < |
|
x − x0 |
|
< δ (ε ) |
|
f ( x) |
|
> ε . |
||||||||
|
|
|
|
|||||||||||||||
|
|
|||||||||||||||||
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) lim f ( x) = ∞ :
x→∞
2) lim f ( x) = +∞ :
x→x0
3) lim f ( x) = −∞ :
x→x0
4) lim f ( x) = +∞ :
x→+∞
Бесконечный предел в бесконечности.
ε > 0 δ (ε ) > 0 x > δ (ε ) f ( x) > εε > 0 δ (ε ) > 0 x − x0 < δ (ε ) f ( x) > ε
ε > 0 δ (ε ) > 0 x − x0 < δ (ε ) f ( x) < −εε > 0 δ (ε ) > 0 x > δ (ε ) f ( x) > ε
33
5) |
lim |
f |
( x) = −∞ : |
"ε > 0 |
$δ (ε ) > 0 |
x < -δ (ε ) |
f ( x) < -ε |
|
||||
|
x→−∞ |
|
( x) = −∞ : |
"ε > 0 |
$δ (ε ) > 0 |
x > δ (ε ) |
f ( x) < -ε |
|
||||
6) |
lim |
f |
|
|||||||||
|
x→+∞ |
|
( x) = +∞ : |
|
"ε > 0 |
$δ (ε ) > 0 x < -δ (ε ) |
f ( x) > ε . |
|
||||
7) |
lim |
f |
|
|
||||||||
|
x→−∞ |
|
|
|
|
|
|
|
|
|
|
|
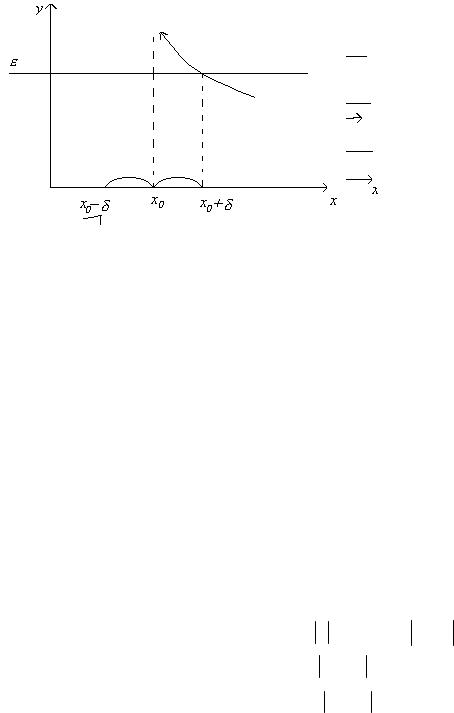
Геометрическая иллюстрация бесконечного предела в бесконечности |
||||||||||||
ε − δ lim f ( x) = +∞ |
lim f |
( x) = −∞ |
lim f ( x) = +∞ |
|
||||||||
|
x→+∞ |
|
x→−∞ |
|
|
x→−∞ |
|
|
||||
на |
ε − δ |
lim f ( x) = +¥ lim f ( x) = -¥ |
lim f ( x) = −∞ . |
|
||||||||
|
|
|
x→x0 |
|
x→x0 |
|
|
x→+∞ |
|
|
||
|
|
|
|
Свойства пределов функции в точке. |
|
|||||||
|
Пусть y = f ( x) |
и y = g ( x) |
- две функции, имеющие конечные пределы |
|||||||||
в точке х0, т.е. |
|
|
|
|
lim g ( x) = B , |
|
|
|||||
lim f ( x) = A |
и |
|
|
|
тогда |
функции |
||||||
x→x0 |
|
|
|
|
|
f ( x) |
x→x0 |
|
|
|||
f ( x) ± g ( x), f ( x) × g ( x), |
|
также имеются конечные пределы в точке |
||||||||||
g ( x) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
х0, причем lim |
( f ( x) ± g ( x)) = A ± B = lim |
x→x0 |
x→x0 |
lim f ( x) × g ( x) = lim f ( x) × lim g ( x) = A × B |
||||||
x→x0 |
|
|
|
|
x→x0 |
x→x0 |
|
f ( x) |
|
A |
|
lim f ( x) |
, B ¹ 0, g ( x) ¹ 0, |
lim |
= |
= |
x→x0 |
|||
|
|
|
||||
x→x0 g ( x) |
|
B lim g ( x) |
|
|||
|
|
|
|
|
x→x0 |
|
f ( x) ± lim g ( x)
x→x0
"x Î X .
Доказательство этих свойств следует из аналогичных свойств для последовательностей и определения предела функции в точке по Гейне.
Предельный переход в неравенства.
Пусть y = f ( x) и y = g ( x) имеют конечные пределы в точке х0, тогда
1) |
если |
f ( x) < g ( x), |
"x Î X lim f ( x) £ lim g ( x) |
|
|
|
f ( x) £ g ( x), |
x→x0 |
x→x0 |
2) |
если |
"x Î X lim f ( x) £ lim g ( x) |
||
|
|
f ( x) > g ( x), |
x→x0 |
x→x0 |
3) |
если |
"x Î X lim f ( x) ³ lim g ( x) |
||
|
|
f ( x) ³ g ( x), |
x→x0 |
x→x0 |
4) |
если |
"x Î X lim f ( x) ³ lim g ( x) . |
||
|
|
|
x→x0 |
x→x0 |
Доказательство следует из соответствующей теоремы о переходе к пределу в неравенствах для последовательностей.
Теорема о зажатой функции.
Если две функции y = f ( x) |
и y = g ( x) имеют одинаковые конечные |
|
пределы в точке х0, т.е. |
|
|
lim f ( x) = lim g ( x) = A |
|
|
x→x0 |
x→x0 |
|
и некоторая функция z ( x) |
f ( x) £ z ( x) £ g ( x) "x Î X , то функция |
|
z(х) имеет тот же конечный предел в точке х0, т.е. lim z ( x) = A .
x→x0
34

БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ. Функция f(х) называется бесконечно малой функцией в точке х0, если
"ε > 0 $δ (ε ) > 0 0 < |
|
x - x0 |
|
< δ (ε ) |
|
α ( x) |
|
< ε |
lim α ( x) = 0 . |
|
|||
|
|
|
|
|
|||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
α ( x) |
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
= |
|
||
Сравнение двух бесконечно малых функций |
lim |
|
|
|
|||||||||
β ( x) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
x→x0 |
|
c - const |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α ( x) бесконечно малая более высокого порядка малости по отношению к β ( x) (обозн. α ( x) = 0(β ( x)) - 0 малое)
¥ α ( x) бесконечно малая более низкого порядка, чем β ( x) .
const α ( x) и β ( x) одного порядка малости α ( x) = 0(β ( x)) - 0 большое 1 α ( x) и β ( x) эквивалентны. α ( x) β ( x) .
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1) сравнить две бесконечно малые α ( x) = x - 2, |
β ( x) = x2 - 4 в точке х0 |
||||||||||||||||||||
lim |
α ( x) |
|
= lim |
|
|
x - 2 |
|
|
= lim |
1 |
|
= |
1 |
α ( x) = 0(β ( x)) |
|||||||
β ( x) |
|
|
|
|
|
|
|
|
|
||||||||||||
x→x0 =2 |
x→2 ( x - 2)( x + 2) |
|
x→2 x + |
2 4 |
|
|
|||||||||||||||
2) α ( x) = sin ( x +1), |
β ( x) = x +1 х0= –1 |
|
|
|
|
|
|||||||||||||||
lim |
|
α ( x) |
|
= lim |
sin ( x +1) |
= lim |
sin t |
=1 β ( x) |
х+1=t ®0 |
||||||||||||
|
β ( x) |
|
|
||||||||||||||||||
x→x0 =−1 |
|
x→−1 x +1 |
|
x→0 |
t |
|
|
|
|
|
|
|
|||||||||
3) α ( x) = x2 , β ( x) = x x = 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
x2 |
|
= lim x = 0 α ( x) = 0 |
(β ( x)) . |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
x→0 x |
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Функция f(х) |
называется |
бесконечно большой в точке х0, если |
|||||||||||||||||
"ε > 0 $δ (ε ) > 0 0 < x - x0 < δ (ε ) f ( x) > ε
|
lim f ( x) = ¥ . |
|
|
|
x→x0 |
|
|
|
Связь между бесконечно большой и бесконечно малой функциями. |
||
|
Если α ( x) - Б.М. в точке х0, α ( x) ¹ 0 в окрестности точки х0 |
||
1 |
= f ( x) - Б.Б. в точке х0. |
|
|
α ( x) |
|
||
|
|
|
|
|
1 |
= α ( x) - Б.М. в точке х0. |
|
|
Если f(х) – Б.Б. в точке х0, |
|
|
|
f ( x) |
||
Понятие производной функции в точке.
Производная функции f(х) в точке х0 называется предел отношение приращения функции к приращению аргумента при стремлении последнего к нулю.
35
f ¢( x |
) = lim |
Df ( x) |
. |
(*) |
|
||||
n |
x→0 Dx |
|
||
|
|
|||
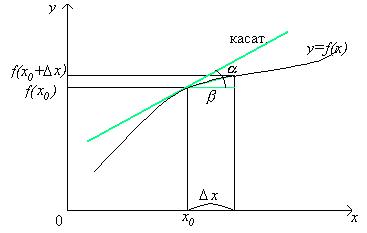
Геометрический смысл производной.
Df ( x) = f ( x0 + Dx) - f ( x0 ) = Dy
tg β = |
y |
Dx ® 0 tg β ® tgα , a - угол наклона |
|
Dx |
|
f ′( x |
) = tgα . |
|
0 |
|
|
Геометрически производная функции в точке х0 есть тангенс угла наклона касательной, построенной к графику функции в точке (х0, f(х)), к оси абсцисс.
Понятие дифференциальной функции.
Функция у = f(х) называется дифференцируемой в точке х0, если предел
(*) существует и кончен. В противном случае функция называется не дифференцируемой.
Если функция у = f(х) дифференцируема в каждой точке множества х, то функция называется дифференцируемой на множестве х.
Теорема о представлении дифференцируемой на некотором множестве функции.
Пусть функция у = f(х) дифференцируема на некотором множестве х, тогда для нее на этом множестве справедливо
|
Df ( x) = A × Dx = α (Dx) , где A = const, α (Dx) - Б.М. функция, |
||||||||||
|
lim α (Dx) = 0 . |
|
|
|
|
|
|||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
В силу дифферен-ти функции у = f(х) имеем |
|
|
|
|||||||
"x Î X |
f |
¢( x |
) = lim |
y |
= A - const lim Dy |
- A |
|
= 0 α% (Dx) - Б.М. |
|||
|
0 |
|
0 |
|
|
x→0 |
Dx |
|
|
|
|
|
|
|
|
|
|
x→0 Dx |
|
|
|
||
функция |
|
|
|
|
|
|
|
|
|
|
|
% |
(Dx) = |
y |
- A |
|
×Dx |
Dx |
% |
|
|
|
|
|
|
|
|
||||||||
α |
Dx |
|
×α (Dx) = Dy - A × Dx |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Dy = A × Dx + Dx ×α% (Dx) α (Dx) α (Dx) = Dx ×α% (Dx)
36
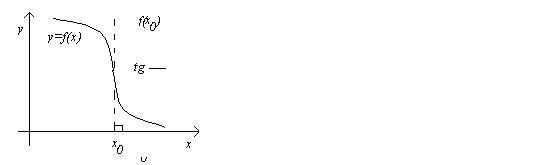
lim α ( x) = 0
x→0
Dy = A × Dx +α (Dx)
lim α ( x) = 0 .
x→0
Связь между непрерывностью и дифференцируемостью функции. Теорема.
Если функция у = f(х) дифференцируема на Х, то она непрерывна на этом множестве.
Обратное неверно, т.е. если функция непрерывна на Х, то она не обязательно дифференцируема на этом множестве.
Дано: f(х) – дифференцируема. Доказать: f(х) – непрерывна.
Определение № 2. lim y = 0 .
x→0
Доказательство:
Воспользуемся представлением дифференцируемой функцией
Df ( x) = A × Dx +α (Dx) , A − const, lim α ( x) .
x→0
Перейдем в этом соотношении к пределу
lim Dy = lim ( A × Dx + α ( x)) = A × 0 + 0 = 0 опр. №2 функция f(х) непрерывна.
x→0 x→0
Вторую часть теоремы проиллюстрируем на чертеже
Таблица производных основных элементарных функций.
у = c.
f(x) = c c - const
(c)¢ = 0 f ¢( x |
) = lim |
f ( x0 + Dx) - f ( x0 ) |
= lim |
c - c |
= 0 . |
|
|
||||
0 |
x→0 |
Dx |
x→0 Dx |
||
|
|||||
у = ln x.
f(x) = ln x Х – область определения
37

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x0 |
+ Dx) - f ( x0 ) |
|
|
|
|
|
|
ln ( x0 + Dx) - ln x0 |
|
|
ln |
x0 + Dx |
|
|
|||||||||||||||||||||||||||
"x0 Î X |
|
|
f ¢( x0 ) = lim |
f |
= lim |
|
= lim |
x0 |
= |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
Dx |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Dx®0 |
|
|
|
|
|
|
|
|
|
Dx®0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx®0 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
×Dx × |
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
Dx Dx |
|
|
|
|
|
|
|
|
Dx Dx |
Dx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
= lim ln |
1 + |
|
|
|
|
= lim ln |
1 + |
x0 |
|
|
|
|
= lim ln e |
0 = |
|
|
|
|
|
× ln e = |
|
|
. |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Dx®0 |
|
|
|
|
|
|
x0 |
|
Dx®0 |
|
|
|
x0 |
|
|
|
|
|
Dx®0 |
|
|
|
|
|
x0 |
|
|
|
x0 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
f ¢( x ) = |
1 |
|
|
|
|
"x Î Xπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
0 |
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(ln x)¢ = |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Аналогично можно доказать формулы для вычисления производных |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
основных элементарных функций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
10. (c)¢ = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
70. (cos x)¢ = -sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
20. (xα )¢ = α × xα -1 |
|
|
|
|
|
|
|
|
|
80. (tgx)¢ = |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
30. (ax )¢ = ax × ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
90. (ctgx)¢ = - |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
(ex )¢ = ex |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100. (arc sin x)¢ = |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 - x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
40. (loga |
x)¢ = |
|
1 |
|
|
|
|
|
|
|
|
|
110. (arccos x)¢ = - |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 - x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
50. (ln x)¢ = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
120. (arctgx)¢ = |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
60. (sin x)¢ = cos x |
|
|
|
|
|
|
|
|
|
130. (arcctgx)¢ = - |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
¢ |
|
1 |
|
|
|
¢ |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
. |
( x)¢ =1 |
|
|
|
|
= - |
|
|
|
( x ) |
= |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Основные правила дифференцирования. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Если u(х) и v(x) некоторые дифференцируемые на множестве Х |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
функции, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1) (c ×u ( x))¢ = c ×u¢( x), |
c - const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
2)(u ( x) ± v ( x))¢ = u¢( x) ± v ( x)
3)(u ( x) × v ( x))¢ = u¢( x) × v ( x) + u ( x) × v¢( x)
|
u ( x) ¢ |
u¢( x)v ( x) - u ( x)v¢( x) |
|
||
4) |
|
|
= |
|
. |
v ( x) |
v2 ( x) |
||||
38
Производные от гиперболических функций. Гиперболическим синусом sh х называется функция, определяемая
соотношением
shx = |
ex - e− x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ e− x |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Гиперболическим косинусом shx = |
ex |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Гиперболический тангенс thx = |
shx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
chx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Гиперболический котангенс cthx = |
chx |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
shx |
|
|
|
|
|
|
|
|
|
|
|
||
(shx)¢ = |
1 |
(ex |
|
- e− x )¢ = |
1 |
(ex + e− x ) = chx (shx)¢ = chx |
|
|
(chx)¢ = shx |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
shx |
¢ |
sh¢xchx - shxch¢x |
|
ch2 x - sh2 x |
|
|
|
|
2 |
|
|
1 |
|
|
|||||||||||||||||||||||||
(thx)¢ = |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
=1 - th |
|
x = |
|
|
|
. |
|||||||||||
|
|
|
|
ch |
2 |
x |
|
|
|
|
ch |
2 |
x |
|
|
|
ch |
2 |
|
|||||||||||||||||||||
|
ctx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||||
|
|
chx ¢ |
|
sh2 x - ch2 x |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
(cthx)¢ = |
|
|
|
== |
|
|
|
|
|
|
|
=1 |
- cth |
|
x = - |
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
sh |
2 |
x |
|
|
sh |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
stx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Дифференцирование сложной функции. |
|
|
|
||||||||||||||||||||||||||
Теорема. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пусть функция |
у(u) |
дифференцируема в точке |
|
u0, причем u0(х0), а |
|||||||||||||||||||||||||||||||||||
функция u(х) дифференцирована в точке х0, тогда производная сложной функции y (u ( x)) по переменной Х находится по формуле
′ |
′ |
′ |
yx |
= yu ×ux . |
|
Пример: |
|
|
y = 5sin2 x |
y = 5sin2 x × ln 5 × 2sin x × cos2 x = sin 2x5sin2 x × ln 5 . |
|
Дифференцирование неявно заданной функции
Функция у = f(х) называется заданной неявно, если известно некоторое функциональное соотношение, связывающее переменные х и у вида F ( x, y ) = 0 , причем если известно явное выражение функции у = f(х), то при
подстановке этого выражения в соотношение F ( x, y ) = 0 получается тождество, т.е. F ( x, f ( x)) = 0 .
Замечание: при дифференцировании функции, заданной неявно, дифференцируют соотношение F ( x, y ) = 0 при этом считают, что у есть
функция, зависящая от х. Пример:
|
x ′ |
||
y2 ln ( x + y ) − sin |
|
|
= (0)′ |
|
|||
|
y |
|
|
39

( y2 )¢ ln ( x + y ) + y2 ×(ln ( x + y ))¢ |
|
x ¢ |
|
|
|
||||
- sin |
|
= 0 |
|
|
|
||||
|
|
|
|
||||||
|
|
|
y |
|
x′ × y - x × y′ |
|
|||
2 y × y¢ × ln ( x + y ) + y2 × |
1 |
|
(1 +1× y¢) - cos |
x |
× |
= 0 . |
|||
|
|
y |
y2 |
||||||
|
x + y |
|
|
|
|
||||
ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ.
Если функция у = f(х) содержит произведение и частное нескольких корней разной степени или представляет собой показательно-степенную функцию у которой в основании стоит элементарная функция и в степени также элементарная функция, то для нахождения производной такой функции применяют метод логарифмического дифференцирования.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× 7 |
|
( x -1)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x2 + x - 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
Пример: y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
x3 |
+ 5 × 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Шаг № 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Вычислить натуральный логарифм от функции, т.е. получить |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
выражение |
|
ln y = ln f ( x) . |
|
|
|
|
Преобразовать |
|
|
|
правую |
часть полученного |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
выражения согласно свойствам логарифма: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
ln a p = p ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ln (ab) = ln a + ln b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ln |
a |
|
= ln a - ln b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln y = ϕ ( x), ϕ ( x) = ln f ( x), считая, |
|||||||||||||||||||||
2) |
Продифференцировать соотношение |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
что y = y ( x) , т.е. |
1 |
× y¢( x) = ϕ¢( x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3) |
Найти значение y′, y′ = y ×ϕ′( x) = f ( x) ×ϕ′( x) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
(3x |
2 |
+ x - 4) + |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
ln (x |
3 |
+ 5) - |
1 |
|
|
|
|
¢ |
||||||||||||||||||||||||||||||
(ln y )¢ = |
|
|
ln |
|
|
|
|
|
ln ( x |
-1) - |
|
|
|
|
|
|
|
ln ( x -1) |
|||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
7 |
|
|
2 |
|
|
4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
× y¢ = |
1 |
× |
|
1(6x +1) |
+ |
|
3 |
× |
|
|
|
1 |
|
|
- |
1 |
× |
|
1 |
|
|
|
×3x2 - |
1 |
× |
1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
+ |
5 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
y |
|
|
|
|
3 3x2 + x - 4 7 x |
1 2 x3 |
|
|
|
|
|
|
|
4 x -1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x -1)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
3 3x2 |
+ x - 4 × |
|
|
1 |
|
|
|
|
|
|
6x +1 |
|
|
|
3x |
2 |
|
|
|
|
|
|
1 |
|||||||||||||||||||||||||||||||||||||||
|
y¢ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
× |
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
|
+ 5) |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 3x |
|
+ x - 4 |
2 |
|
4 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
+ 5 × |
|
|
x -1 |
|
|
|
|
2 |
3 |
( x -1) |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y = (cos x)tg 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(ln y )¢ = (tg 2 x ln cos x)¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
1 |
× y¢ = |
2tgx |
|
× ln cos x + tg 2 x × |
1 |
|
|
|
×(-sin x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
cos2 x |
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
