
Lectures part1
.pdf
- 41 -
Из табл. 4.1 видно, как меняются напряжения при изменении ориентации сечения согласно (4.16), (4.17).
Таблица 4.1
Ориентация сечения α |
Нормальные |
Касательные |
||||||||
|
напряжения σa |
напряжения τa |
||||||||
0 |
σ = σα max |
|
|
0 |
|
|
|
|||
45° |
σ |
2 |
σ |
2 |
= |
|
t |
α |
|
max |
|
|
|||||||||
|
|
|
|
|
|
|
||||
90° |
0 |
|
|
0 |
|
|
|
|||
В таблице также отмечены и максимальные значения напряжений, кото- рые легко указать, учитывая свойства тригонометрических функций.
Нулевые напряжения для α = 90° показывают, что поперечная деформа- ция происходит без напряжений в поперечном направлении. При увеличении расстояния между частицами (молекулами или атомами) в направлении растя- жения пустоты занимают соседние атомы.
N (x) = P |
Рассмотрим теперь деформацию прямоугольной |
сетки, расположенной под произвольным углом к про- |
|
|
дольной оси (рис. 4.7). Очевидно, что при деформациях |
a |
ε > 0 и εп = −με < 0 углы сетки прямыми не остаются. |
b
b*
c |
Если abc – прямой угол в материале до деформации, то |
||
*a*c* . Введем |
|||
a* |
|||
понятие угловой деформации g с помощью равенства |
|||
|
|||
c* |
g = Ðbac - Ðb*a*c* = π - Ðb*a*c* , |
(4.18) |
|
2 |
|
||
|
|
||
|
из которого видно, что угловая деформация представля- |
||
|
ет собой угол (безразмерная величина), на который в ре- |
||
N (x) = P |
зультате деформации изменяется прямой угол, выделен- |
||
ной в деформируемом теле. |
|
||
Рис. 4.7 |
Угловая деформация связана с касательными на- |
||
|
пряжениями равенством |
|
|
|
τ = G γ , |
(4.19) |
|
называемым законом Гука для сдвига. Входящий в это равенство коэффициент пропорциональности G называется модулем сдвига (или модулем упругости на сдвиг) и связан с модулем на растяжение соотношением
G = |
E |
|
2(1+ m) . |
(4.20) |
- 42 -
Поскольку γ – величина безразмерная, то из (4.19) следует, что модуль упруго- сти измеряется в тех же единицах, что и напряжение.
Соотношения (4.19), (4.20) могут быть получены аналитически из соот- ношений для НДС растянутого стержня. Проводить дополнительный экспери- мент не обязательно. Действительно, по нагрузке мы можем вычислить напря- жения на любых площадках, а также определить перемещения любых точек растянутого стержня, а по ним и интересующие нас углы в деформируемом те- ле. Следовательно, величины τ и γ могут быть выражены через одни и те же величины, что и приводит к соотношениям (4.19), (4.20).
Вывод закона Гука для сдвига
 N (x) = P
N (x) = P
n |
a (a* ) |
α |
m |
 ω 2 c
ω 2 c
ω 1
b f |
c* |
|
b* |
 N (x) = P
N (x) = P
Рис. 4.8
Совместим вершины углов а и а* (рис. 4.8), по- ступательно перемещая угол b*a*c* к углу bac. Из оп- ределения угловой деформации (4.18) и (рис. 4.1) сле-
дует: |
|
γ = ω1 + ω2 . |
(4.21) |
Найдем угол ω1. Для этого запишем длину отрезка fB* как разность осевых перемещений точек а и b (ко- ординату х по-прежнему отсчитываем от одного из концов стержня):
f b * = u(xb ) − u(xa ) = xb ε − xa ε = |
|
= (xb − xa )ε = nb ε = |
|
= (absinα)ε = sε sinα , |
(4.22) |
где s = ab.
Для случая, когда координата y отсчитывается от оси стержня: |
|
||||||||||||
|
|
|
|
|
= v(yb ) − v(ya ) = ybεп − yaεп = (yb − ya )εп = (scosα)εп . |
(4.23) |
|||||||
|
|
f b |
|||||||||||
Учитывая, что εп = −με , для длины отрезка получим |
|
||||||||||||
|
|
|
|
|
= sμεcosα . |
(4.24) |
|||||||
|
|
f b |
|||||||||||
Найдем теперь проекцию ломаной bfb* на отрезок |
|
|
|
||||||||||
ac |
|
||||||||||||
|
|
|
= |
|
*cosα + |
|
sinα . |
(4.25) |
|||||
am |
f b |
f b |
|||||||||||
Этот же отрезок можно записать по-другому |
|
||||||||||||
|
|
= |
|
*sinω1 . |
(4.26) |
||||||||
|
am |
a *b |
|||||||||||
Обозначив
a *b * = s *
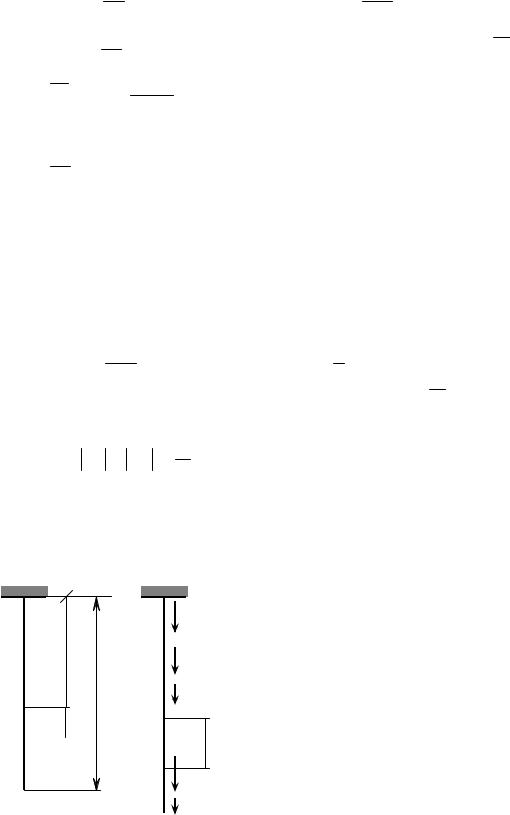
и учитывая, что для малых перемещений и деформаций sinω1 ≈ ω1 , из равенства правых частей (4.25) и (4.26) с учетом (4.22) и (4.24) получим
- 43 -
ω1 = ε ss* (sin α cosα + μ cosα sin α) = ε 2ss* (1 + μ) sin 2α .
Покажем, что ss* ≈ 1. По определению, линейная деформация отрезка ab
ab = εab = s *s−s ,
откуда
ss* = 1+ εab .
Тогда для малых деформаций справедливо
|
s |
|
= |
|
|
1 |
|
≈1. |
|
|
s * |
1 |
|
|
|||||
|
|
+ εab |
|||||||
Для |
луча |
|
формулу, аналогичную (4.27), можно получить, |
||||||
ac |
|||||||||
αac = α + 90° .
(4.27)
есть
(4.28)
если учесть, что
Действительно
ω2 = ε 2ss * (1 + μ) sin 2(α + 90° ) = − 2ε (1 + μ) sin 2α .
Знак минус указывает лишь на направление поворота отрезка ac . Воспользовавшись (4.21) и законом Гука, найдем
γ = ω1 + ω2 = σE (1+ μ)sin2α ,
но
τ = σ2 sin2α ,
поэтому
A
x
l C  x
x D
D 
B
A
C*
D*
B*
qx
 *)x
*)x 
(
γ = 2(1+ μ) τ .
E
Откуда и следуют равенства (4.19) и (4.20).
Данное доказательство справедливо только для случая растяжения-сжатия. Однако закон Гука для сдвига справед-
лив и в общем случае малых перемещений и деформаций трехмерного тела.
Понятие линейной деформации в точ-
ке
Рис. 4.9 |
Рассмотрим стержень на рис. 4.9, растянутый |
|
неравномерно распределенной по его длине нагруз- |
||
|
кой qx (слева тот же стержень до нагружения). Отдельные отрезки его длины
- 44 -
будут, очевидно, деформироваться по-разному.
Уточним и обобщим понятие линейной деформации. Рассмотрим произ- вольную точку C на оси стержня на расстоянии x от опоры и точку D на рас- стоянии x от C. В результате деформации от осевой нагрузки точка C займет положение C* , а точка D – положение D* . Обозначим отрезок
C*D*= ( x)* .
Линейной деформацией в точке С в направлении оси x назовем |
|
|||||||
εx (x) = lim |
C*D* − CD |
= lim |
( x)* − x |
= |
(dx)* − dx |
. |
(4.29) |
|
CD |
x |
dx |
||||||
x→0 |
x→0 |
|
|
|
||||
Использование дифференциалов в конце цепочки равенств вполне правомерно, поскольку выражение содержит предел. Смысл величины (dx)* очевиден: это измененная при деформации длина отрезка dx. Как видно из (4.29), линейная деформация, как и раньше, есть отношение приращения длины к первоначаль- ной длине отрезка. Уточнение заключается в том, что при неравномерной де- формации надо рассматривать бесконечно короткий отрезок.
Зависимость между линейными деформациями и осевыми перемещениями при растяжении
A
C D
B
|
A |
x |
|
|
l |
x |
C* |
d |
|
|
D* |
|
B* |
Рис. 4.10
qx
 (dx)*
(dx)*
Получим зависимость между линейными дефор- мациями и осевыми перемещениями для общего слу- чая неравномерного растяжения стержня. Снова рас- смотрим стержень, растягиваемый неравномерно рас- пределенной по его длине нагрузкой (рис. 4.10), но длину отрезка CD будем сразу считать бесконечно ма- лой, т.е. CD = dx . Это позволит нам не переходить к пределу, а сразу записывать результат для бесконечно малых величин. Занесем в табл. 4.2 координаты точек до и после деформации, используя для записи функ- цию осевых перемещений точек стержня u. (uD обо- значает перемещение точки D).
Таблица 4.2
C |
D |
C* |
D* |
x |
x + dx |
x + u |
x + dx + uD |
Но точки C и D расположены бесконечно близко друг к другу, поэтому, учитывая непрерывность задачи, перемещение в точке D можно выразить через перемещение точки С c помощью терминов анализа бесконечно малых, т.е. с помощью дифференциала:
uD = u + du . |
- 45 - |
(4.33) |
|
||
Запишем теперь по определению (4.29) деформацию в точке C. Посколь- |
||
ку других деформаций здесь не рассматриваем, индекс x опустим |
|
|
e(x) = dx* - dx |
= C*D* - CD . |
(4.34) |
dx |
CD |
|
Подставим сюда длины отрезков, которые легко записать как разность коорди-
нат соответствующих точек, и учтем (4.33): |
|
[dx + du] - dx |
|
||||
e (x) = |
[(x + dx + u + du) - (x + u)] - dx |
= |
. |
||||
|
|
|
dx |
dx |
|||
Отсюда получаем |
|
|
|
|
|||
|
|
|
|
|
|
||
e(x) = du . |
|
|
|
|
|
(4.35) |
|
|
dx |
|
|
|
|
|
|
Очевидно, справедливо и обратное соотношение, которое легко получить |
|||||||
интегрированием равенства (4.295) |
|
|
|
||||
x |
x |
æ du ö |
|
|
|
||
òe(x)dx = ò |
ç |
|
÷dx |
|
|
|
|
|
|
|
|
||||
xн |
xн |
è dx ø |
|
|
|
||
|
|
|
|
|
|
||
откуда |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
òe(x)dx = u(x)- u(xн ) , |
|
|
|
||||
xн |
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
u(x)= u(xн )+ òx e(x)dx . |
|
|
(4.38) |
||||
|
|
|
xн |
|
|
|
|
При растяжении невесомого стержня было принято, что xн = 0, u(xн )= 0,
а также показано, что e = const. Тогда из общего соотношения (4.29) следует полученное ранее соотношение u(x)= εx .
|
|
|
|
|
- 46 - |
|
|
|
|
Тема №5. Диаграммы растяжения-сжатия. Основные механические ха- |
|||||||
|
|
|
рактеристики материалов. Расчет на прочность по допускае- |
|||||
|
|
|
мым напряжениям |
|
|
|
|
|
|
Диаграмма растяжения малоуглеродистой стали. |
|
|
|||||
|
Основные механические характеристики материалов |
|
||||||
|
|
|
|
Для определения механических свойств материалов в |
||||
|
|
|
промышленности проводят испытания на растяжение и |
|||||
|
|
|
сжатие стандартных образцов. Испытывают стержни и на |
|||||
|
|
|
все другие виды деформаций. При этом свойства образцов |
|||||
|
|
|
изучаются не только в пределах действия закона Гука. Об- |
|||||
|
|
|
разцы испытывают до разрушения. |
|
|
|||
|
|
|
|
Для испытаний используются образцы круглого или |
||||
|
|
|
прямоугольного поперечного сечения с головками для за- |
|||||
|
|
|
крепления в захватах испытательной машины (рис. 5.1). |
|||||
|
|
|
Стандарты на образцы для испытаний устанавливаются, |
|||||
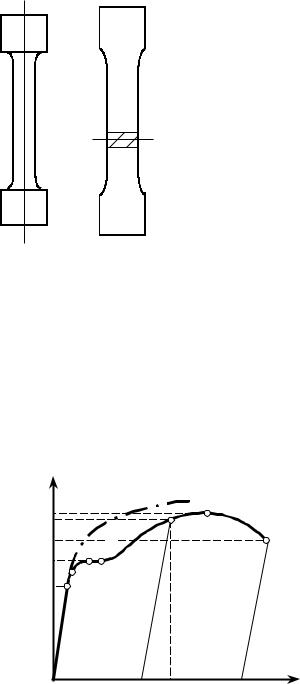
Рис. 5.1 |
|
во-первых, для того, чтобы сделать результаты испытаний |
||||||
|
|
|
сопоставимыми. Действительно, соотношение между дли- |
|||||
ной и поперечными размерами, чистота поверхности образца, форма головок, |
||||||||
зажимаемых в приспособлении и другие параметры влияют в большей или |
||||||||
меньшей степени на результаты испытаний. При использовании стандартных |
||||||||
образцов это влияние уменьшается. Кроме того, стандарты составлены на ос- |
||||||||
нове опыта испытаний и теории, что позволяет избежать ошибок при выборе |
||||||||
параметров образцов и при проведении испытаний. |
|
|
||||||
Рассмотрим результаты испытаний образца из малоуглеродистой стали. |
||||||||
|
P |
|
|
|
Это основной конструкционный мате- |
|||
C1 |
|
|
|
C |
риал в промышленности. |
|
||
|
|
|
На |
рабочей части образца перед |
||||
Z1 K1 |
|
|
Z |
K |
||||
B B* |
|
испытанием наносят |
деления (обычно |
|||||
B1 |
|
|
|
|||||
|
|
|
|
через каждые 5 или 10 миллиметров), |
||||
Y1 |
Y |
|
|
|
||||
|
|
|
чтобы иметь возможность после опыта |
|||||
A1 |
A |
|
|
|
||||
|
|
|
|
|
судить об изменении длины образца. |
|||
|
|
|
|
|
Образец помещают в машину и закреп- |
|||
|
|
|
|
l |
ляют его концы. Медленно перемещая |
|||
|
O |
O1 |
O2 |
O3 O4 |
один конец образца в направлении его |
|||
|
оси, стержень растягивают нагрузкой, |
|||||||
|
|
Рис. 5.2 |
|
|||||
|
|
|
которая |
возрастает |
постепенно, |
без |
||
|
|
|
|
|
||||
- 47 -
толчков и ударов. При опыте отмечают ряд последовательных значений на-
грузки Р и измеряют соответствующее им увеличение длины образца |
l. |
Результаты измерений обычно фиксируются машиной в виде |
так назы- |
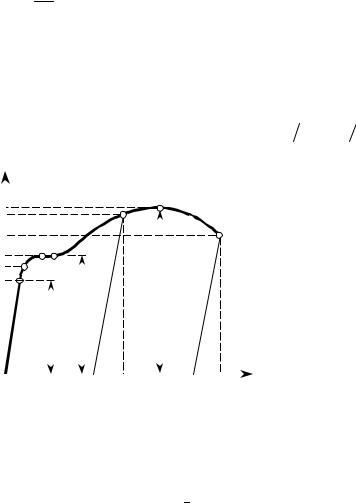
ваемой машинной диаграммы растяжения. При вычерчивании диаграммы по вертикальной оси откладываются в определенном масштабе нагрузки Р, а по горизонтальной – абсолютные удлинения l.
Рассмотрим диаграмму, полученную при испытании образца из малоуг- леродистой стали (рис. 5.2). Первая часть диаграммы до некоторой точки А яв- ляется почти прямой линией. Ордината ОА1 представляет собой значение рас- тягивающей силы, превышение которой вызывает отклонение от закона пря- мой линии, соответствующей закону Гука.
При увеличении растягивающей силы деформация начинает расти быст- рее нагрузки – диаграмма приобретает криволинейный вид с выпуклостью вверх. Далее наблюдается резкое изменение в работе материала; при некотором значении растягивающей силы ОB1 для увеличения деформации почти не нуж- но увеличивать растягивающую силу, говорят, что материал "течет". На диа- грамме образуется горизонтальная (или почти горизонтальная) площадка BB*.
Во время течения материала на поверхности образца появляются в более или менее резкой степени так называемые линии Чернова-Людерса. Эти линии вы- зываются взаимными перемещениями частиц материала при наступлении зна- чительных деформаций образца.
При проведении испытаний на особо точном оборудовании можно обна- ружить, что закон Гука является приближенной зависимостью. Незначительные отклонения от него (от прямой линии) наблюдаются уже при относительно не- больших нагрузках. Рост деформаций всегда несколько опережает рост нагру- зок, и прямая плавно переходит в кривую.
После образования площадки текучести материал вновь начинает сопро- тивляться дальнейшему растяжению, и для увеличения удлинения l прихо- дится увеличивать силу. Точка C диаграммы соответствует наибольшему зна- чению нагрузки.
В этот момент поведение образца еще раз резко меняется. До этого в уд- линении участвовал весь стержень; каждая единица его длины увеличивалась примерно одинаково; точно так же во всех сечениях было одинаковое умень- шение поперечных размеров образца.
С момента, когда нагрузка достигает величины ОC1, деформация в основ- ном сосредоточивается в одном месте образца; небольшой участок образца
около этого места подвергается в дальнейшем большему усилию на единицу площади поперечного сечения, т.е. большему напряжению; это влечет за собой
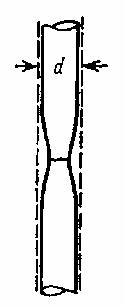
- 48 -
местное сужение поперечного сечения, образуется так называемая "шей-
ка" (рис. 5.3).
Вследствие уменьшения площади в деформирующейся части для даль- нейшего удлинения образца нужна все меньшая и меньшая сила. Наконец, при нагрузке ОК происходит разрыв.
Если приостановить опыт при нагрузке, меньшей ОА1, и разгрузить об- разец, то при разгрузке зависимость между силой и удлинением будет выра- жаться той же прямой, что и при нагрузке ОА1. После удаления нагрузки удли- нение исчезает, – происходила лишь упругая деформация. О
свойстве упругости уже говорилось при рассмотрении закона Гука.
Если мы произведем разгрузку образца от некоторой точ- ки Z диаграммы, лежащей между B* и C, то при разгрузке диа- грамма будет изображаться прямой ZO1, примерно парал- лельной прямой ОА. Таким образом, образец в этом случае по- сле снятия нагрузки (если нет нагрузки, его можно вынуть из машины) не вернется к первоначальным размерам; отрезок OO1 будет представлять необратимое удлинение образца, на- зываемое остаточным удлинением. При новом нагружении диаграмма снова пройдет примерно по той же прямой ZO1 до точки Z, затем до точки C и далее. Как видим, отрезок O1O2 является упругим удлинением, которое полностью исчезает при снятии нагрузки. Это удлинение по-прежнему пропорцио-
нально нагрузке с тем же модулем упругости (наклоном линии диаграммы). Сумма отрезков OO1 и O1O2 – полное удлинение при нагрузке ОZ1. Иногда ука- зывают ещё нагрузку ОY1, до которой происходят лишь упругие деформации. Соответствующая точка Y диаграммы лежит выше точки А, которой отмечен конец прямолинейного участка диаграммы. Положение точки Y определяется допущением о точности, с которой проверяется отсутствие остаточных удли- нений. Поскольку закон Гука является приближенной зависимостью, ее поло- жение полностью зависит от принятой точности. В значительной мере это от- носится и к точке А, однако малые остаточные удлинения трудно измерять и контролировать, поэтому точку Y редко выделяют и используют. Для опреде-
ления же положения точки А стандарт предусматривает несложную методику (о ней скажем ниже), без которой положение точки А также нельзя указать од- нозначно.
Как видим, за точкой A образец начинает необратимо менять свою форму.
Пластичностью называется свойство материала необратимо менять
- 49 -
свою форму, не разрушаясь.
Наибольшее значение растягивающей образец силы изображается орди- натой ОC1; она часто называется разрушающей нагрузкой, так как необходима для того, чтобы началось разрушение. Если бы нагрузку создавал вес какого- либо груза, то после точки C начался бы процесс разрушения с ускорением. Но
поскольку испытательные машины имеют фиксированные скорости активного захвата, то получаем диаграмму процесса разрушения, которое наступает при нагрузке, изображаемой на диаграмме ординатой точки К.
Машинная диаграмма, приведенная на рис. 5.2, характеризует свойства образца, а не материала. Чтобы получить свойства материала необходимо пе- рейти к относительным величинам. Будем делить нагрузки на первоначальную площадь поперечного сечения F0, а абсолютные удлинения на первоначальную длину растягиваемого участка образца l0. Вместо машинной диаграммы полу- чим такую же по характеру кривую, выражающую зависимость между напря- жением:
σ = P ,
F0
и относительным удлинением (линейной деформацией):
|
ε = l l . |
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
Отличаться от машинной диаграммы полученная кривая будет только по- |
||||||||
стоянными масштабными множителями 1 F0 и 1 l0 . |
|
||||||||
|
|
σ |
|
|
|
|
|
По осям полученной |
диаграммы |
c1 |
|
|
|
c |
(рис. 5.4), которая называется условной |
||||
|
|
|
|||||||
|
|
|
|
||||||
|
|
|
|
диаграммой растяжения, откладываются |
|||||
z1 |
|
|
|
z |
|
k |
соответственно величины σ и ε. Услов- |
||
|
|
|
|
||||||
k1 |
|
|
|
|
|||||
|
b |
b* |
|
||||||
b1 |
|
|
|
|
ной эта диаграмма называется потому, |
||||
y1 |
|
y |
|
|
|
|
|
что при ее построении используются |
|
|
|
|
|
|
|
||||
a1 |
|
a |
|
в |
|
|
|
||
|
т |
σ |
|
|
|
данные о геометрии образца до начала |
|||
|
|
пц |
σ |
|
|
|
|
||
|
|
|
|
|
|
испытаний. Можно догадаться, что это |
|||
|
|
σ |
|
|
|
|
|
||
|
|
|
|
|
ε |
не вполне точно. |
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Характерные точки, |
намеченные |
|
O |
|
o1 o2 |
|
o3 o4 |
||||
|
|
|
на машинной диаграмме, перенесем на |
||||||
|
|
|
|
|
|
|
|
||
|
|
|
Рис. 5.4 |
|
|
|
условную диаграмму σ - ε, заменив со- |
||
|
|
|
|
|
|
|
|
ответствующие буквы строчными. Эти |
|
точки и принимаются, по существу, за механические характеристики материа- ла. Например, под пределом пропорциональности понимается наибольшее нор- мальное напряжение, до которого приближенно сохраняется линейная за-
- 50 -
висимость между σ и ε. В качестве предела пропорциональности по ГОСТу 1497-84 принимают:
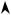 P
P
Pтв
Pтн
0 |
l |
|
Рис. 5.5 |
Pтв |
P |
|
|
Pтн |
|
0 |
l |
Предел пропорциональности σпц - напряже- ние, при котором отступление от линейной зави-
симости между нагрузкой и удлинением достигает такой величины, что тангенс угла наклона, образо- ванного касательной к кривой "нагрузка-удлинение" в точке Рпц с осью нагрузок увеличивается на 50% от своего значения на упругом (линейном) участке.
Наименьшее напряжение, при котором обра- зец деформируется без заметного увеличения рас- тягивающей нагрузки, называется физическим пре- делом текучести σт.
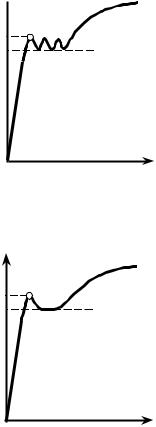
Отметим, что у сталей более сложного состава
может быть и более сложная форма диаграммы в зоне текучести (например, такая, как на рис. 5.5 и 5.6). Первый пик усилий в начале текучести назы-
вают зубом текучести. Напряжение, соответст- вующее первому пику усилий, называют верхним пределом текучести σтв , а наименьшее напряже-
ние в зоне текучести называют нижним пределом текучести σтн .
Временным сопротивлением (пределом проч- ности) σв называется напряжение, соответст-
вующее наибольшей нагрузке, предшествующей разрыву образца.
Кроме указанных напряжений ГОСТы определяет другие механические характеристики материалов, например, модули упругости на растяжение и сдвиг.
Модуль упругости Е – это отношение приращения напряжения к соот- ветствующему приращению удлинения в пределах упругой деформации.
Модуль сдвига G – это отношение касательного напряжения к упругой угловой деформации в точке.
Модуль сдвига определяется при испытаниях на кручение.
Заметим, что при испытаниях по ныне действующим стандартам опреде- ляются именно эти две величины, а коэффициент Пуассона – пересчётом. По-
скольку
G = |
E |
|
, |
2 1 + μ |
) |
||
|
( |
|
