Lectures part1

Министерство образования и науки Российской Федерации Федеральное агентство по образованию

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н. ТУПОЛЕВА

А.Ю. ОДИНОКОВ

ЛЕКЦИИ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ (Часть 1)

Под редакцией члена-корреспондента АН РТ В.Н. Паймушина

Учебное пособие

Рекомендовано к изданию Учебно-методическим центром КГТУ им. А.Н. Туполева

Казань 2007

УДК 539.3 / .6 ББК 30.121

А.Ю. Одиноков. Лекции по сопротивлению материалов (часть 1). Учеб- ное пособие /. Под редакцией члена-корреспондента АН РТ В.Н. Паймушина. Казан. гос. техн. ун-т. Казань, 2007. 180 с.

Излагаются только важнейшие вопросы первой части курса сопротивле- ния материалов: построение эпюр внутренних силовых факторов, растяжение и сжатие стержней, система уравнений теории упругости, положения теории на- пряженно-деформированного состояния в точке, плоский чистый и поперечный изгиб, срез и кручение стержней. Предназначено для студентов технических вузов.

Рецензенты: докт. физ.-мат. наук, проф. В.А. Иванов (Казан. гос. техноло- гический университет)

докт. физ.-мат. наук, проф. Р.А. Каюмов (Казан. гос. архи- тектурно-строительный университет)

©Изд-во Казан. гос. техн. ун-та, 2007 ©А.Ю. Одиноков, 2007

- 3 -

Тема №1. ВВЕДЕНИЕ

Содержание курса "Сопротивление материалов" и его место среди

других дисциплин

Учебная дисциплина "Сопротивление материалов" изучает вопросы, вхо- дящие в общую физическую науку – механику. Сопротивление материалов раз- вивает положения теоретической механики, в которой рассматриваются абсо- лютно твердые тела, на случай деформируемых тел, которые под нагрузкой к тому же могут разрушаться. Соответственно новому объекту изучения ставятся и новые задачи, чрезвычайно важные для практики, решаются вопросы прочно- сти, жесткости, устойчивости конструкций и другие.

Под проверкой прочности понимается, конечно, проверка того, выдержи- вает ли конструкция приложенную к ней нагрузку без разрушения.

При проверке жесткости проверяется, не выходят ли перемещения точек конструкции (или другие параметры, характеризующие ее деформированное состояние) под действием нагрузки за пределы допускаемых значений.

Об устойчивости деформируемых тел мы будем говорить позже, так как это явление менее знакомо нам из жизненного опыта, а пояснить его в двух словах, не рассмотрев важнейшие положения курса, затруднительно.

Не лишним будет сказать, зачем эта наука нужна инженеру-механику. Без нее невозможно грамотно спроектировать ни одну машину, ни одно технологи- ческое приспособление. Даже если не надо ничего проектировать или рассчи- тывать, инженеру бывает важно просто понять, как ведет себя конструкция под нагрузкой, где, как и отчего она может разрушиться, с чего начинается ее раз- рушение, как она деформируется (гнется) и т.д.

Не изучавшему данный курс будет трудно указать, где наиболее нагру- женные точки в балке на рис. 1.1 и как они нагружены.

P

Рис. 1.1

По-видимому, первая научная работа по сопротивлению материалов при- надлежит Галилео Галилею (1638 год). Сооружения и машины до этого созда- вали без расчетов прочности и жесткости, исходя просто из опыта, что, конеч- но, возможно только в относительно простых случаях.

Однако до 19-го века наука развивалась медленно, отчасти из-за трудно-

- 4 -

стьи названных проблем. К 19-му веку развитие промышленности сделало не- обходимым получение решений этих задач. В начале 19-го века французским ученым Навье были наконец преодолены принципиальные трудности и сфор- мулированы гипотезы и подходы, позволяющие успешно решать эти задачи. В результате наука стала быстро развиваться, и к 20-м годам 20-го века учебные курсы по этой науке были уже примерно такими, как и сейчас, и охватывали практически все основное содержание науки.

Последняя, однако, не стояла на месте, а интенсивно развивалась. В ре- зультате, учебная дисциплина, сопротивление материалов, стала частью об- ширной области знания, которую наиболее логично, по-видимому, называть механикой деформируемого твердого тела (МДТТ).

Ее место среди других учебных дисциплин можно представить с помо- щью следующей табл.1.1

Таблица 1.1

I. Теоретическая механика

II. Механика сплошной среды

МДТТ - часть более общего раздела механики, механики сплошной среды, куда входят также механика жидкости, газа, плазмы.

МДТТ имеет также другое название – строительная механика, причем к строи- тельству эта наука имеет лишь то отноше-

Рис. 1.2 ние, что широко используется в том числе и при расчете зданий и сооружений.

- 5 -

Сопротивление материалов исторически первая часть МДТТ. Естествен- но, она включает в себя решение наиболее простых, но и самых практически

и трехмерные.

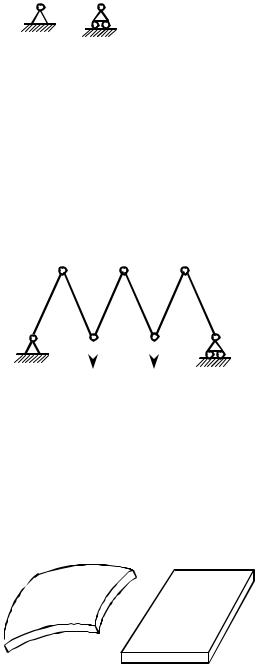
Как известно, широко используются конструкции, представляющие собой стержневые системы. Выделяют два основных типа таких систем: 1) рамы, 2) фермы. Рамами называют стержневые системы, стержни которых (пря- молинейные и криволинейные) жестко соединены между собой и работают в том числе на изгиб и кручение. Стержневая конструкция на рис. 1.3 является рамой.

позволяет снять моментное нагружение одного стержня другим. В результате в стержнях ферм нет внутренних моментов. (В реальных фермах в узлах может не быть шарниров, и тогда такая конструкция несколько отличается от идеаль- ной фермы. Однако моментное нагружение стержней всё же оказывается вто-

- 6 -

Однако чаще строительную механику стержневых систем в учебных кур- сах объединяют с теорией пластин и оболочек и называют этот курс строитель- ной механикой.

Оболочками называют тела, один размер которых значительно меньше двух других (рис. 1.5). Если лицевые поверхности плоские, то такие тела назы-

вают пластинами.

Расчет оболочек приводит к задачам с двумя независимыми переменными (координатами), которые, конечно, много сложнее одномерных.

Трехмерные тела изучает теория упругости. Эта наука появилась в 19-м веке и развивалась одновременно с сопротивлением материалов. В отличие от сопротивления материалов теория упругости использует с самого начала стро- гие математические построения высокой сложности. Поэтому она долго оста- валась в значительной мере наукой для науки. Практические решения от нее стали получать в основном в 20-м веке, особенно после появления вычисли- тельных машин и развития численных методов. Но зато эта наука является тео- ретическим обоснованием и фундаментом сопротивления материалов.

Ясно, что сопротивление материалов и теория упругости имеют общие разделы. Из теории упругости возьмем лишь то, что надо для сопротивления материалов, т.е. для решения одномерных задач и понимания получающихся результатов.

Специальные вопросы прочности, особые приемы расчета отдельных ти- пов конструкций, например самолетов, рассматриваются в курсах расчета прочности самолетов, судов, ракет и т. д. Эти дисциплины обычно присутству- ют в учебных планах соответствующих специальностей.

Отдельные разделы МДТТ составляют такие науки, как теория пластич- ности и ползучести, механика разрушения и др. Эти разделы обычно либо вхо- дят в уже названные учебные дисциплины, либо могут входить в учебные пла- ны отдельной строкой.

Естественно, что МДТТ и сопротивление материалов как раздел механи- ки опираются на общие построения теоретической механики, изучающей абсо- лютно твердые тела. Широко используется аппарат элементарной и высшей ма- тематики. Кроме того, сопротивление материалов использует также некоторые общие данные материаловедения. Поэтому знание этих дисциплин необходимо для изучения сопротивления материалов.

Таким образом, "Сопротивление материалов" является по существу вве- дением в МДТТ для инженеров.

Само же название "Сопротивление материалов" традиционное, сложилось исторически и, по-видимому, не очень четко отражает содержание науки.

- 7 -

Постановка задач сопротивления материалов

Задачи, которые решаются в курсе «Сопротивление материалов», могут быть сведены к следующим типам. Прежде всего, это прямая (основная) задача расчета конструкций, постановка которой такова: известна геометрия конст- рукции, свойства ее материалов, нагрузка, требуется проверить ее прочность, жесткость и устойчивость.

Кроме того, часто приходится решать обратные задачи, задачи проекти- рования. В отличие от прямой задачи они могут иметь много разных постано- вок. Например: известны часть размеров конструкции, свойства ее материалов, нагрузка, требуется определить недостающие размеры из условий прочности, жесткости и устойчивости.

Другой вариант постановки обратной задачи: известна геометрия конст- рукции, свойства ее материала, требуется определить наибольший допустимый уровень нагрузки по условиям прочности, жесткости и устойчивости.

Может показаться по этим формулировкам, что одна из задач чисто условно названа прямой, а другая обратной. Но в действительности за этими названиями скрываются принципиальные различия в математической формулировке задач, при- чем обратные задачи отличаются в общем случае значительно большей сложностью.

Расчетные схемы и математические модели

Во всяком исследовании реальную конструкцию приходится упрощать, отбрасывая мало влияющие на точность расчета факторы. Расчетная схема это есть упрощенная модель конструкции, в которой отброшены несущественно влияющие на результат данного расчета детали. Математическое описание расчетной схемы называют математической моделью конструкции. Ни один расчет не может быть абсолютно точным, это всегда результат выбора той или иной расчетной схемы, всегда только приближение к реальности, более или ме- нее точное. Дополнительная погрешность может вноситься и математической моделью конструкции.

Выбор расчетной схемы и построение математической модели – исклю- чительно важный, сложный и требующий квалификации этап работы. Если слишком упростить задачу, результат получится с недопустимой ошибкой, если ее переусложнить, то решение может оказаться либо слишком дорогим, либо его вообще не найдешь.

Мы не будем обстоятельно рассматривать этот вопрос из-за ограниченно- сти объема курса, с одной стороны, с другой стороны, будем применять всего одну, так называемую балочную расчетную схему, а из-за недостатка времени

- 8 -

изучим только один вариант соотношений для этой расчетной схемы.

Заметим, что брус на бумаге будем изображать, как правило, всего одной линией оси бруса, в качестве которой выберем линию центров тяжести попе- речных сечений. (Почему именно эту линию будет ясно из теории изгиба стержней.) В дальнейшем для бруса будем всегда использовать правую систему координат, а ось x направлять вдоль оси бруса, причем плоские задачи будем рассматривать в плоскости x0y.

Изображение бруса в виде одной линии не означает, что реальный брус бесконечно тонкий. Балочная расчетная схема даст хорошие результаты в большинстве задач, если отношение высоты бруса к его длине меньше, чем 1 : 10, удовлетворительные же результаты возможны даже при отношениях

1 : 5.

Схематизация конструкции (т.е. построение ее расчетной схемы) не за- канчивается принятием балочной расчетной схемы, необходима дальнейшая схематизация геометрии конструкции: надо принять конкретные размеры кон- струкции, которые всегда заданы с допуском, отбросить несущественные эле- менты. Схематизации подлежат также опоры конструкции, нагрузка на нее и свойства материала, из которого она изготовлена. Рассмотрим часть из этих во- просов.

Схемы опирания

Детали конструкции в большинстве случаев соединены с другими дета- лями. При рассмотрении одной из них все прочие детали, с которыми соедине-

щательная. Именно плоские задачи и будем в основном решать в нашем курсе, чтобы познакомить с основами науки, ее понятиями и методами. Предполагаем,

что на основе полученных знаний специалист сможет самостоятельно решать с помощью соответствующей литературы более сложные задачи, в том числе

- 9 -

пространственные.

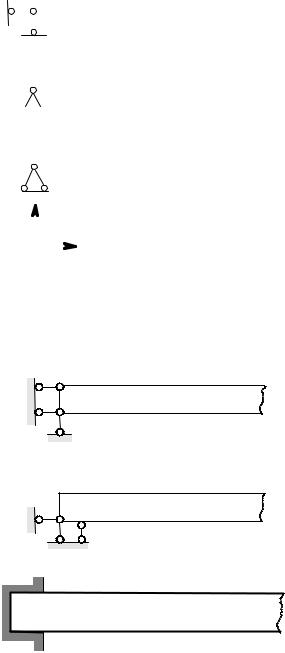
При схематизации опирания обычно учитывают в первую очередь коли- чество степеней свободы, которые блокирует данное опорное устройство, или, как еще говорят, сколько внешних связей накладывает данная опора. Каждая

дополнительно наложенная внешняя связь может быть представлена в виде стержня, соединяющего через шарниры рассматриваемую деталь с опорной по-

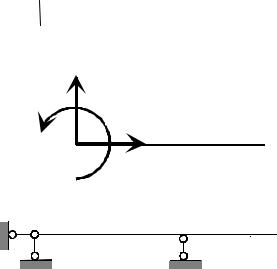
её изображения даны на рис. 1.9. В такой опоре возникают в общем случае две опорные реакции R гор и R вер , а опорный момент не возникает.

получается, например, если конец балки замурован в стену (рис. 1.11). Эта опо- ра называется защемлением или заделкой. Ее условное изображение дано на

- 10 - (рис. 1.12). В виде трех стержней заделку не изображают. Но надо иметь в виду,

что опоры на рис. 1.10 и 1.12 по существу эквивалентны. В заделке возникают в общем случае три опорные реакции: две силы R гор и R вер и момент MR

(рис. 1.13).

Вполне очевидно, что реальная связь конструкции с опорой сложнее этих

Укажем, что для закрепления балки в плоском случае минимально необ- ходимы три связи. Такое опирание чаще всего обеспечивается либо одним за- щемлением балки на одном из ее концов (рис. 1.12), либо двумя шарнирными опорами, одна из которых подвижна (рис. 1.14).

Балка на рис. 1.12 называется консольной; консолью называется также часть балки, выступающая за опоры (рис. 1.14). Часть балки между опорами называется пролётом.

Возможно наложение и большего числа опорных связей, чем это мини- мально необходимо, но тогда опорные реакции невозможно найти из уравнений статики, т.е. уравнений равновесия. В этом случае получаются так называемые

статически неопределимые задачи, но о них мы будем говорить позднее.

Силы в сопротивлении материалов, их классификация.

Остановимся на некоторых понятиях сопротивления материалов, касаю- щихся нагрузки и её схематизации.

Различают следующие виды сил:

1. Силы внешние и внутренние. Внутренние силы это силы, действующие между частями рассматриваемого деформируемого твердого тела. Внешние си- лы (или внешняя нагрузка) это силы, которые действуют извне на рассматри-