
- •Введение
- •Глава 1. Множества, отношения и функции
- •1. Задание множества
- •2. Операции над множествами
- •3. Разбиение множества. Декартово произведение
- •4. Отношения
- •5. Операции над отношениями
- •6. Функция
- •7. Отношение эквивалентности. Фактор-множество
- •8. Отношения порядка
- •9. Вопросы и темы для самопроверки
- •10. Упражнения
- •Глава 2. Алгебраические структуры
- •1. Операции и предикаты
- •2. Алгебраическая система. Алгебра. Модель
- •3. Подалгебры
- •4. Морфизмы алгебр
- •5. Алгебра с одной операцией
- •6. Группы
- •7. Алгебра с двумя операциями. Кольцо
- •8. Кольцо с единицей
- •9. Поле
- •10. Решетки
- •11. Булевы алгебры
- •12. Матроиды
- •13. Вопросы и темы для самопроверки
- •14. Упражнения
- •Глава 3. Булевы функции
- •2. Формулы
- •3. Упрощения в записях формул
- •4. Равносильность формул
- •5. Важнейшие пары равносильных формул
- •6. Зависимости между булевыми функциями
- •7. Свойства операций штрих Шеффера, стрелка Пирса и сложения по модулю два
- •8. Элементарные суммы и произведения. Конституенты нуля и единицы
- •9. Дизъюнктивные и конъюнктивные нормальные формы
- •10. Представление произвольной булевой функции в виде формул
- •11. Совершенные нормальные формы
- •12. Полином Жегалкина
- •13. Сокращенные дизъюнктивные нормальные формы
- •14. Метод Квайна получения сокращенной д.н.ф.
- •15. Тупиковые и минимальные д.н.ф.
- •16. Метод импликантных матриц
- •17. Минимальные конъюнктивные нормальные формы
- •18. Полнота системы функций. Теорема Поста
- •21. Функциональная декомпозиция
- •22. Вопросы и темы для самопроверки
- •23. Упражнения
- •Глава 4. Элементы комбинаторики
- •1. Правило суммы для конечных множеств
- •2. Правило произведения для конечных множеств
- •3. Выборки и упорядочения
- •5. Число всевозможных разбиений конечного множества. Полиномиальная теорема
- •6. Метод включения и исключения
- •7. Задача о беспорядках и встречах
- •8. Системы различных представителей
- •9. Вопросы и темы для самоконтроля
- •10. Упражнения по комбинаторике
- •Глава 5. Теория графов
- •1. Основные типы графов
- •2. Изоморфизм графов
- •3. Число ребер графа
- •4. Цепи, циклы, пути и контуры
- •5. Связность графа. Компоненты связности
- •6. Матрица смежности
- •7. Матрицы смежности и достижимости
- •8. Критерий изоморфизма графов
- •9. Матрица инциденций
- •10. Деревья
- •11. Задача о минимальном соединении
- •12. Центры дерева
- •13. Ориентированные деревья
- •14. Эйлеровы графы
- •15. Гамильтоновы графы
- •16. Планарные графы
- •17. Задача о кратчайшей цепи между произвольными вершинами графа
- •18. Алгоритм Дейкстры нахождения кратчайших путей от заданной вершины орграфа
- •19. Потоки в сетях
- •20. Вопросы и темы для самопроверки
- •21. Упражнения
- •Список литературы

31
Глава 2. АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ
Некоторые результаты по алгебраической тематике дошли до нас в клинописных текстах древнего Вавилона, например, относящихся ко времени правления династии Хаммурапи (18001600гг. до н. э.), в работах мыслителей древнего Египта, Греции, Индии, Китая и Арабского Востока.
В работе Аль-Хорезми «Китаб мухтасар аль-джебр на-л-мукабала» алгебра впервые рассматривается как самостоятельный раздел математики. Название операции «аль-джебр», состоящей в переносе членов из одной стороны уравнения в другую с изменением знака,
впоследствии стало названием раздела
Аль-Хорезми
математики (алгебра).
§ 1. Операции и предикаты
Ранее было введено понятие функции f:A→B, где множество А может быть любым, например может быть декартовым произведением каких-то
множеств, положим А=С×С или А=С×С×С, или А= C × C × ...× C = С n.
1442443
n − раз
Если множество А является декартовым произведением n множеств, то аргументом функции f: A→B является упорядоченная n-ка, например, (x1,x2,…,xn), xi C, 1≤ i ≤ n. Таким образом, n-аргументная, n≥ 1, функция
у=f(x1,x2,…,xn) отображает С n в (на) B.
Функцию ϕ: С n→ С называют n-арной (n-местной) операцией на С или операцией с n аргументами.
Например, функция f(x,y)=x+y есть 2 - местная операция – операция сложения, а функция ϕ(x,y)=x·y – 2 - местная операция умножения на множестве действительных чисел.
32
Предикат был определен ранее как некоторое логическое утверждение, зависящее от х. Теперь зная, что такое функция, предикат можно ввести, используя понятие функции.
Предикатом от n аргументов (n - местным предикатом) называется
функция с областью определения C × C × ...× C , n≥1, и областью значений,
1442443
n − раз
равной множеству {И, Л}; здесь И – истина, Л – ложь. Итак, n- местный предикат Р отображает С n в (на) множество {И, Л}.
Рассмотрим примеры. Пусть А={… ,-2, -1, 0, 1, 2, …} и положим, что Р(х) обозначает: "х – четное число". Тогда при х=2 получим, что Р(2)=И, а при х=3 Р(3)=Л и т.д.
Пусть С=(-∞,∞), А=С×С и Р(х,у) обозначает х > у. Тогда Р(3,1)=И,
Р(3,5)=Л и т.д.
§ 2. Алгебраическая система. Алгебра. Модель
Алгебраической системой называют непустое множество А с введенными на этом множестве операциями и предикатами, т.е. алгебраическая система это упорядоченная тройка:
А= A;ΩF,ΩP ,
где
А – непустое множество;
ΩF – множество операций; каждая операция Fi (Fi ΩF) имеет mi
аргументов, mi ≥ |
0. При mi > 0 операция Fi отображает множество |
A × A × ...× A = Ami |
в (на) А. При mi = 0 – Fi (функция константа) определяется |
14243 |
|
mi − раз |
|
фиксированным элементом из А. Операции Fi (Fi ΩF) называются главными операциями системы;
ΩP – множество предикатов, такое, что каждый предикат Pj из ΩP имеет
n (n ≥ 1) аргументов из А. Предикат P отображает множество A × A × ...× A = j j j 14243
n j − раз
Anj в (на) множество {И, Л}; предикаты Рj (Рj ΩP) называются главными предикатами системы.
Таким образом, можно записать (при mi > 0):
F |
Pj |
i |
A × A × ...× A → {И, Л}. |
A × A × ...× A → A, |
|
14243 |
14243 |
mi − раз |
n j − раз |
Множество А называется носителем или основным множеством, а его элементы - элементами системы. Алгебраическая система называется конечной, если конечно множество А.

33
Алгебраическая система A;ΩF,ΩP называется алгеброй, если ΩP= и
ΩF ≠ и моделью (реляционной системой), если ΩF = и ΩP ≠ .
Следовательно, алгебру можно ввести следующим образом.
Алгебра – непустое множество А, на котором задана совокупность операций, переводящих элементы из А в А.
Пример. Пусть А = (0,∞) и введем операции +, ×, /, 
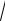 . В результате
. В результате
имеем алгебру положительных вещественных чисел.
Будем рассматривать алгебры с конечным числом операций.
Пусть имеем алгебру с n операциями F1, F2,…, Fn и пусть mi число аргументов операции Fi (1≤ i≤ n). Тогда вектор τ = (m1, m2,…, mn) называют типом алгебры. Так, рассмотренный пример алгебры имеет тип τ = (2,2,2,1).
Рассмотрим еще один пример. Пусть А = {…, -2, -1, 0, 1, 2, …} и на этом множестве введены две операции: + и ×. Ясно, что тип алгебры равен: τ = (2,2).
§ 3. Подалгебры
Пусть имеем алгебру A; ΩF , здесь ΩF – множество n операций на непустом множестве А. Положим, что тип алгебры есть (m1, m2,…, mn).
Подмножество В множества А называется замкнутым относительно операции Fi, если Fi переводит элементы из В в это же В, т.е. для x1, x2,…,
xmi B имеет место, что Fi(x1, x2, …, xmi) B.
Если подмножество В (В А) замкнуто относительно всех операций алгебры, то В= B; ΩF называют подалгеброй алгебры A; ΩF . Иногда вместо В говорят, что В - подалгебра, подразумевая, что на В определены те же операции, что и для всей алгебры.
Пусть А=[0,∞) и введем операции сложения (+) и умножения (×). Множество натуральных чисел N = {0, 1, 2, …} содержится в А и замкнуто относительно операций + и ×. Поэтому N порождает подалгебру в алгебре
[0,∞);+,× .
Теорема 2.1 Пересечение любой совокупности подалгебр данной алгебры либо пусто, либо является подалгеброй данной алгебры.
Доказательство. Пусть имеем некоторое множество подалгебр {Bk} данной алгебры A; ΩF . Рассмотрим пересечение этих подалгебр и пусть это пересечение равно В (B=∩Bk). Если В= , то утверждение теоремы доказано. Пусть В≠ . Выберем произвольную операцию Fi из ΩF и произвольные элементы x1,x2,…,xmi из В. Так как В - пересечение всех подмножеств Bk, то элементы x1,x2,…,xmi принадлежат каждому Bk и так как Bk - подалгебра, то
34
Fi(x1,x2,…,xmi) Bk. В результате получаем, что Fi(x1,x2,…,xmi) B, т.е. В подалгебра. Теорема доказана.
Рассмотрим алгебру А = {1,2,3,…},+ . Пусть А1={2,4,6,…} и А2={3,6,9,…}. Очевидно, что А1 и А2 порождают подалгебры данной алгебры и пересечения этих подалгебр тоже является подалгеброй. Объединение множеств А1 и А2 равно:
А1 А2={2,3,4,6,8,9,…}.
Полученное множество А1 А2 не замкнуто относительно операции сложения, ибо, например, 2+3=5, но 5 (А1 А2). Таким образом, объединение подалгебр не всегда является подалгеброй данной алгебры.
§ 4. Морфизмы алгебр
Будем рассматривать однотипные алгебры
А = A; ΩF и В = B, ΩG ,
где
ΩF = (F1, F2, …, Fn), τ =(m1,m2,…,mn), mi – число аргументов Fi; ΩG = (G1, G2, …, Gn), τ =(m1,m2,…,mn), mi – число аргументов Gi.
Таким образом, рассматриваем алгебры, в каждой из которых введены одинаковые числа (n) операций и для каждого i, 1≤ i ≤ n, числа аргументов операций Fi и Gi одинаковы.
Всякое отображение ϕ основного множества А в(на) основное множество В называем отображением алгебры А в(на) алгебру В.
Изоморфизмом алгебры А = A; F1, F2, …, Fn в(на) однотипную алгебру В = B; G1, G2, …, Gn называется взаимно однозначное (биективное) отображение ϕ множества А в(на) В, сохраняющее главные операции алгебры, т.е. для которого выполняются соотношения:
ϕ(Fi(x1, x2, …, xmi))=Gi(ϕ(x1), …, ϕ(xmi)) |
(2.1) |
|||
для всех i, 1≤ i ≤ n, и для любых x1, x2,…, xmi A. |
|
|||
Изоморфизм алгебры на себя называется автоморфизмом. |
||||
Гомоморфизмом алгебры А = A; F1, F2, …, Fn в(на) однотипную |
||||
алгебру В = B; G1, G2, …, Gn называется отображение ϕ множества А в(на) |
||||
множество В, сохраняющее главные |
|
|||
операции алгебры, т.е. для которого |
y=ln x |
|||
выполняются условия (2.1) для всех i, 1≤ i ≤ |
|
|||
n, и для любых x1, x2,…, xmi A. |
|
|||
Пусть А= (0,∞); × , В= (-∞,∞);+ . |
x |
|||
Обе алгебры имеют тип τ = (2). Рассмотрим |
|
|||
отображение ϕ(х) = ln(x) множества (0,∞) на |
|
|||
множество |
(-∞,∞). |
График функции ln(x) |
Рис. 2.1 |
|
приведён |
на рис. |
2.1. Это отображение |
||
|
||||
|
|
|
|
35 |
|
|
|
|
|
является взаимно однозначным отображением множества (0,∞) на множество |
|||||||||
(-∞,∞). Выясним, сохраняется ли операция, т.е. будет ли произведение |
|||||||||
переходить в сумму. Имеем: |
|
|
|
|
|
|
|
||
|
ϕ(a×b)=ln(a×b)=ln a+ln b=ϕ(a)+ϕ(b). |
|
|
|
|
|
|||
|
Таким образом, образ произведения равен сумме образов |
||||||||
сомножителей. Следовательно, отображение ϕ(х)=ln(x) в данном случае |
|||||||||
является изоморфизмом А на В. |
|
|
|
|
|
|
|
||
|
Пусть А = (0,∞); + , В= (-∞,∞); |
|
|
|
|
|
|||
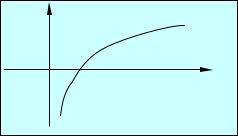
× . Введем отображение ϕ(х)=ех. График |
|
|
|
|
|
||||
функции ех приведён на рис. 2.2. Тогда |
|
|
|
y=e |
x |
||||
имеем: ϕ(х+у) = ех+у = ех еу = ϕ(х) ϕ(у). |
|
|
|
|
|||||
|
|
|
|
|
|||||
Таким образом, образ суммы равен |
|
|
|
|
|
||||
произведению образов. |
Следовательно, |
|
|
|
|
x |
|||
это отображение является изоморфизмом |
|
|
|
|
|||||
|
|
|
|
|
|||||
А |
в В, так как ϕ отображает взаимно |
|
|
|
|
|
|||
однозначно множество (0,∞) на часть |
|
|
|
Рис. 2.2 |
|||||
множества (-∞,∞), ибо ех >1 . |
|
|
|
|
|
|
|
||
|
Пусть А = {0, 1, 2, …}; + , В = {0, 1, 2, ..., 9}; +10 , где +10 есть |
||||||||
сложение по модулю 10 (3+4=7, 3+8=1, 3+9=2, … , т.е. из результата |
|||||||||
вычитается кратное десяти). Построим отображение у=ϕ(х), где у равняется |
|||||||||
остатку от деления х на 10 (если х=10, то у=0, если х=19, то у=9). Это |
|||||||||
отображение ϕ не является взаимно однозначным, |
ибо ϕ(10)= ϕ(30)=0, |
||||||||
ϕ(11)= ϕ(31)=1 и т.д. Теперь проверим, сохраняет ли ϕ операцию, т.е. будет |
|||||||||
ли выполняться равенство ϕ(n+k)= ϕ(n) +10 ϕ(k). Имеем: |
|
||||||||
|
n + k = q 10 + r = n + |
k = q 10 + r + q |
2 |
10 + r = |
|||||
|
10 |
10 |
10 |
1 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
= ( q1 + q2 )×10 + r1 + r2 , r1 ≤ 9,r2 ≤ 9. |
|
|
|
|
||||
Теперь имеем, что ϕ(n+k) = r = r1 +10 r2 = ϕ(n) +10 ϕ(k). |
|
|
|||||||
|
Таким образом, это отображение сохраняет операцию, следовательно, |
||||||||
является гомоморфизмом. |
|
|
|
|
|
|
|
|
|
|
Пусть М - множество квадратных n×n матриц действительных чисел и |
||||||||
на М введена операция умножения матриц, т.е. имеем алгебру А = M; × типа |
|||||||||
τ = (2). Положим, что В = (-∞,∞);• , здесь «•» означает обычное умножение |
|||||||||
чисел. Введем отображение ϕ(С)=det(С), когда матрице С ставится в |
|||||||||
соответствие ее определитель (det(С)). Очевидно, имеем |
|
||||||||
|
ϕ(С×D)= det(C×D)= detС• detD= ϕ(C)• ϕ(D). |
|
|
|
|
||||
