155

Теперь попытаемся определить для произвольного графа наименьшее число цепей, таких, что никакие две из них не имеют общих ребер, а все они вместе покрывают весь граф. Ясно, что если в графе имеется такое семейство цепей, то каждая нечетная вершина должна быть либо начальной, либо конечной точкой, по крайней мере, одной из них, иначе вершина была бы четной. Как известно, число нечетных вершин графа четно, скажем равно 2k. Значит, каждое семейство цепей, покрывающих граф, должно состоять, по крайней мере, из k цепей. Покажем теперь, что существование 2k нечетных вершин является и достаточным условием существования k таких цепей.

Теорема 5.19. На любом связном графе с 2k нечетными вершинами имеется семейство из k цепей, которые в совокупности содержат все ребра графа в точности по одному разу.

Доказательство. Обозначим нечетные вершины графа, взятые в некотором порядке, через A1,A2,…,Ak; B1,B2,…,Bk. Если добавим к нашему графу k ребер (A1,B1),(A2,B2),…,(Ak,Bk), то все вершины станут четными и на нем существует эйлеровый цикл C. При удалении добавленных ребер цикл C распадется на k отдельных цепей, содержащих все ребра графа.

В уме своем я создал мир иной И образов иных существованье;

Я цепью их связал между собой, … М. Лермонтов

§ 15. Гамильтоновы графы

Эйлеровы графы характеризуются тем свойством, что существуют циклы, содержащие каждое ребро один раз. Гамильтоновы циклы определяются для связных графов аналогичным образом, но только по отношению к вершинам:

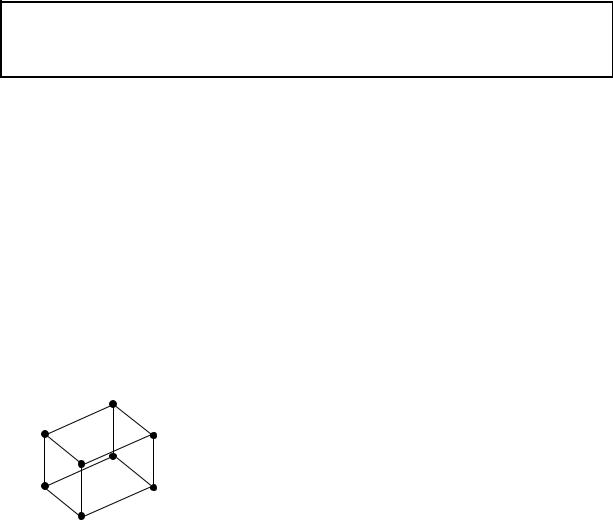
цикл называется гамильтоновым, если он проходит через каждую вершину графа один и только один раз. Гамильтоновым графом называется граф,

содержащий гамильтонов цикл. На рис. 5.27 приведен граф, вершинами которого являются вершины параллелепипеда, а ребрами – все рёбра

Рис. 5.27 этого параллелепипеда. Этот граф является гамильтоновым графом; ребра, порождающие гамильтонов цикл, на этом рисунке изображены сплошной линией.

Гамильтоновой цепью в графе называется простая цепь, проходящая через каждую вершину графа один и только один раз.

Несмотря на сходство в определениях для эйлеровых и гамильтоновых циклов (графов), соответствующие теории для этих понятий имеют мало общего. Критерий существования эйлеровых циклов был установлен просто. Для гамильтоновых циклов не получены необходимые и достаточные

156

условия. Более того, даже для конкретных графов бывает очень трудно иногда практически решить, можно ли найти такой цикл.

Приведём некоторые достаточные условия существования гамильтоновых циклов, т.е. условий, при которых граф является гамильтоновым. Пусть граф G имеет n вершин v1, v2, …, vn и пусть di=deg(vi), i=1,2,…,n - локальные степени его вершин. Будем считать, что вершины обозначены таким образом, что d1≤ d2 ≤ …≤ dn. Можно доказать следующую теорему.

Теорема 5.20 (Хватал, 1972 г.). Пусть граф G имеет n вершин v1, v2, …, vn, d1≤ d2 ≤ …≤ dn и n ≥ 3. Если для любого k верна импликация

dk ≤ k < n/2 dn-k ≥ n-k,

то граф G гамильтонов.

Из этой теоремы можно получить следующее нетривиальное следствие. Следствие 5.1. Пусть граф G имеет n вершин v1, v2, …, vn, d1≤ d2 ≤ …≤ dn

иn ≥ 3. Граф G гамильтонов, если выполнено одно из условий:

1)dk ≥ n/2 для любого k=1,2,…,n (теорема Дирака, 1952);

2)deg(u)+deg(v) ≥ n для любых двух различных несмежных вершин u и v графа G (теорема Оре, 1960);

3)dk ≥ k для любого натурального числа k такого, что 1≤ k ≤ n/2.

Орцикл орграфа, проходящий через каждую его вершину, называется

гамильтоновым орциклом. Орграф называется гамильтоновым, если он обладает гамильтоновым орциклом. Напомним, что через обозначается число дуг, входящих в вершину v, а deg-(v) - число дуг, исходящих из вершины v. Можно доказать следующий аналог теоремы Дирака.

Теорема 5.21 (Гуйя-Ури). Пусть G – орсвязный граф с n вершинами. Если deg+(v) ≥ n/2 и deg-(v) ≥ n/2 для любой его вершины v, то G - гамильтонов орграф.

Твой путь? – переспросила Королева.

- Не знаю, что ты хочешь этим сказать! Здесь все пути мои!

Л. Кэрролл

§ 16. Планарные графы

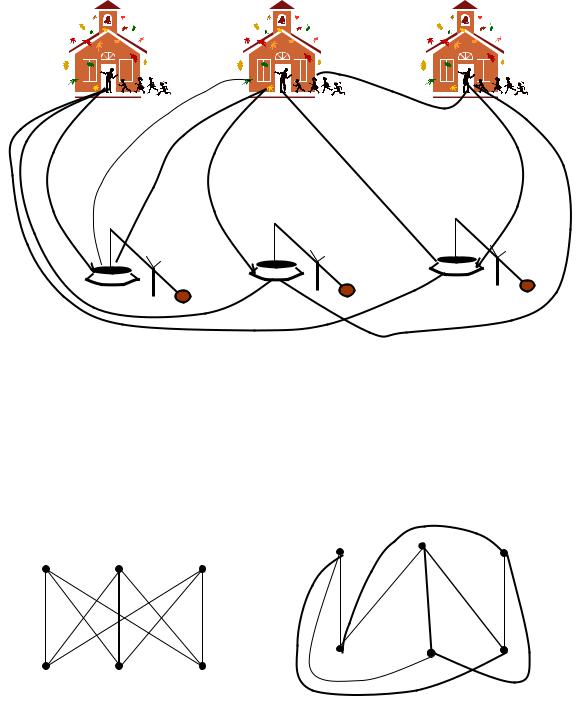
Рассмотрим известную задачу (головоломку) о трех домах и трех колодцах. На одном участке построены три дома и имеется три колодца. Колодцы часто пересыхают, поэтому важно, чтобы от каждого дома имелся

157

путь к каждому из колодцев. Так как обитатели домов в ссоре, то желательно, чтобы пути к колодцам не пересекались. См. рис. 5.28.

Обозначим дома через А, В и С, а колодцы – через X, Y и Z. На рис. 5.29 приведены два варианта возможных расположений тропинок от домов до колодцев.

Рис. 5.28

При варианте дорог, изображенных на рис. 5.29, а), имеется много пересечений. В следующем случае, см. рис. 5.29, б) осталось только одно пересечение. Можно ли сделать так, чтобы пересечений дорог (троп) не было. Ясно, что задачи, аналогичные этой, возникают не только для перессорившихся соседей. В печатных платах важно научиться проводить соединения без пересечений (без необходимости), также это важно для скоростных автомобильных дорог и т.п.

Рис. 5.29

158

Плоским графом называется граф, изображенный на плоскости так, что никакие два его ребра (или, вернее, представляющие их линии) не пересекаются нигде, кроме инцидентной или обоим вершины

Граф изоморфный плоскому графу, называется планарным графом.

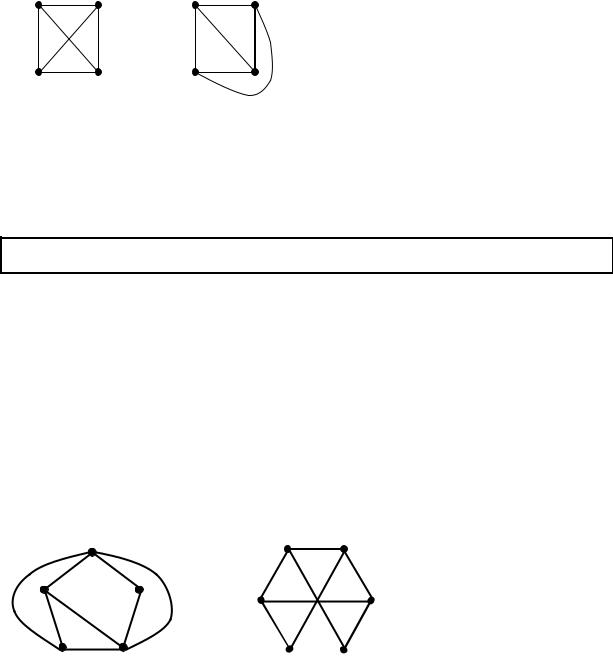
На рис. 5.30 изображены два графа; оба они планарные, но плоский только один из них, который расположен справа. Пусть К5 – полный граф с пятью вершинами, а К3,3 – полный двудольный граф с шестью вершинами, множество вершин которого разбито на два подмножества: V1 и V2. Множества V1

и V2 содержат по три вершины, и каждая вершина из V1 соединяется ребром с каждой из V2, и наоборот, каждая вершина из V2. соединяется ребром с каждой из V1.

Теорема 5.20. Графы К5 и К3,3 непланарны.

Доказательство. Докажем для К5. Так как К5 - полный граф, то он содержит цикл длины 5, который можно записать v1 v2 v3 v4 v5 v1 и без потери общности считать, этот цикл изображается правильным пятиугольником, см. рис. 5.31, а). Ребро (v5,v2) лежит либо целиком внутри пятиугольника, либо целиком вне его. Рассмотрим случай, когда (v5,v2) лежит внутри пятиугольника (второй случай будет аналогичным). Поскольку (v1,v4) и (v1,v3) не пересекают (v5,v2), то они должны лежать вне пятиугольника. Ребро (v3,v5), очевидно, должно быть внутри пятиугольника. Тогда как ни проводить ребро (v4,v2), оно обязательно пересекается либо с (v3,v5), либо с (v1,v3). Таким образом, граф К5 непланарен.

Рассмотрим граф К3,3. Пусть V1={v1,v3,v5}, V2={v2,v4,v6}. По условию v1 соединено с v2, v2 с v3, v3

159

одновременно либо внутри, либо вне шестиугольника и поэтому они обязательно пересекаются. Теорема доказана.

Ясно, что каждый граф, содержащий К5 и К3,3, не является планарным. Оказывается, что К5 и К3,3 – по существу единственные непланарные графы в том смысле, что любой непланарный граф «содержит» один из них. Чтобы

Теорема 5.23 (теорема Куратовского - Понтрягина). Граф планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного К5 или

К3,3.

Доказательство. Необходимость. Графы К5 и К3,3 непланарные, поэтому если граф содержит подграф, гомеоморфный любому из них, он также непланарен. Достаточность примем без доказательства.

Операция включения в ребра графа новых вершин со степенями 2 называется расширением графа. Определим операцию стягивания графа.

Пусть х = (v,u) ребро графа G, не являющееся петлёй. Элементарным стягиванием называется такая процедура: удаляем ребро х, отождествляя вершину v с вершиной u, отбрасываем все петли графа и отождествляем кратные рёбра. В результате получим некоторый граф G*, который считаем полученным элементарным стягиванием ребра х = (v,u). На рис. 5.33

приведены графы G1 и G2, а также графы G* и G* , полученные операцией

1 2

элементарного стягивания из G1 и G2 соответственно.

Граф G называется стягиваемым к графу H, если H можно получить из G с помощью некоторой последовательности элементарных стягиваний.

Примем без доказательства следующую теорему.

Теорема 5.24 (Вагнер, Харари, Татт). Граф планарен тогда и только тогда, когда он не содержит подграфов, стягиваемых к К5 или к К3,3.

Толщиной графа G называется наименьшее число планарных графов, объединение которых даёт G.