
- •Введение
- •Глава 1. Множества, отношения и функции
- •1. Задание множества
- •2. Операции над множествами
- •3. Разбиение множества. Декартово произведение
- •4. Отношения
- •5. Операции над отношениями
- •6. Функция
- •7. Отношение эквивалентности. Фактор-множество
- •8. Отношения порядка
- •9. Вопросы и темы для самопроверки
- •10. Упражнения
- •Глава 2. Алгебраические структуры
- •1. Операции и предикаты
- •2. Алгебраическая система. Алгебра. Модель
- •3. Подалгебры
- •4. Морфизмы алгебр
- •5. Алгебра с одной операцией
- •6. Группы
- •7. Алгебра с двумя операциями. Кольцо
- •8. Кольцо с единицей
- •9. Поле
- •10. Решетки
- •11. Булевы алгебры
- •12. Матроиды
- •13. Вопросы и темы для самопроверки
- •14. Упражнения
- •Глава 3. Булевы функции
- •2. Формулы
- •3. Упрощения в записях формул
- •4. Равносильность формул
- •5. Важнейшие пары равносильных формул
- •6. Зависимости между булевыми функциями
- •7. Свойства операций штрих Шеффера, стрелка Пирса и сложения по модулю два
- •8. Элементарные суммы и произведения. Конституенты нуля и единицы
- •9. Дизъюнктивные и конъюнктивные нормальные формы
- •10. Представление произвольной булевой функции в виде формул
- •11. Совершенные нормальные формы
- •12. Полином Жегалкина
- •13. Сокращенные дизъюнктивные нормальные формы
- •14. Метод Квайна получения сокращенной д.н.ф.
- •15. Тупиковые и минимальные д.н.ф.
- •16. Метод импликантных матриц
- •17. Минимальные конъюнктивные нормальные формы
- •18. Полнота системы функций. Теорема Поста
- •21. Функциональная декомпозиция
- •22. Вопросы и темы для самопроверки
- •23. Упражнения
- •Глава 4. Элементы комбинаторики
- •1. Правило суммы для конечных множеств
- •2. Правило произведения для конечных множеств
- •3. Выборки и упорядочения
- •5. Число всевозможных разбиений конечного множества. Полиномиальная теорема
- •6. Метод включения и исключения
- •7. Задача о беспорядках и встречах
- •8. Системы различных представителей
- •9. Вопросы и темы для самоконтроля
- •10. Упражнения по комбинаторике
- •Глава 5. Теория графов
- •1. Основные типы графов
- •2. Изоморфизм графов
- •3. Число ребер графа
- •4. Цепи, циклы, пути и контуры
- •5. Связность графа. Компоненты связности
- •6. Матрица смежности
- •7. Матрицы смежности и достижимости
- •8. Критерий изоморфизма графов
- •9. Матрица инциденций
- •10. Деревья
- •11. Задача о минимальном соединении
- •12. Центры дерева
- •13. Ориентированные деревья
- •14. Эйлеровы графы
- •15. Гамильтоновы графы
- •16. Планарные графы
- •17. Задача о кратчайшей цепи между произвольными вершинами графа
- •18. Алгоритм Дейкстры нахождения кратчайших путей от заданной вершины орграфа
- •19. Потоки в сетях
- •20. Вопросы и темы для самопроверки
- •21. Упражнения
- •Список литературы
|
|
|
|
|
|
|
|
134 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 1 0 |
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поэтому |
вычисляем |
матрицу A 3 |
= |
0 2 0 1 |
|
× |
|
1 |
0 |
1 |
0 |
= |
||||||
1 0 2 0 |
|
|
0 |
1 |
0 |
1 |
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 1 0 1 |
|
|
|
0 |
|
||||
0 |
2 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
3 |
0 |
|
Для |
полученной |
матрицы (1,4)–й |
элемент |
равен 1, |
|||||||||
|
0 |
3 |
0 |
2 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
следовательно, расстояние между 1-й и 4-й вершинами графа G2 равно трём (минимальной степени матрицы А2 при котором (1,4)-й её элемент отличен от
нуля) и имеется ровно одна цепь длины 3, ибо (1,4)-й элемент матрицы A |
3 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
равен единице. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
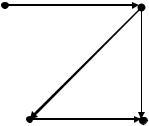
Рассмотрим граф G3, диаграмма которого представлена на рис. 5.13, в). |
||||||||||||||||||||||
Матрица смежности А3 графа G3 равна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
0 1 0 1 |
|
|
|
2 0 2 0 |
|
|
|
0 4 |
0 |
4 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 1 0 |
. Тогда: А |
2 |
0 2 0 2 |
, |
3 |
4 0 |
4 |
0 |
|
|||||||||||||
А = |
0 |
1 |
0 |
1 |
|
|
= |
2 |
0 |
2 |
0 |
|
А |
= |
0 |
4 |
0 |
4 |
. |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0 |
|
|
1 0 1 0 |
|
|
|
0 2 0 2 |
|
|
|
4 0 |
|
|
||||||||||||
По матрице А2 можно определить, что из вершины v1 до вершины v3 имеется две цепи длины 2: v1 - v2 - v3 и v1 - v4 - v3. По матрице А3 можно определить, что из вершины v1 до вершины v2 имеется четыре цепи длины 3: v1 – v4 - v3 –
v2, v1 – v2 - v3 – v2, v1 – v2 – v1 – v2 и v1 – v4 – v1 – v2.
Матрица смежности остовного подграфа G* графа G, очевидно, равна: А(G*)=J - А(G), где J - матрица смежности полного графа, состоящая полностью из единиц, за исключением элементов диагонали.
Логика стала математической, математика логической. Вследствие
этого сегодня совершенно невозможно провести границу между ними. В сущности, это одно и то же.
Б. Рассел
§ 7. Матрицы смежности и достижимости
Матрицу смежности графа (орграфа) с n вершинами вводят и как логическую n× n матрицу L = (lij), такую, что:
для графа:
|
135 |
|
|
|
И, |
если вершины vi |
и vj |
соединены ребром, |
|
lij = |
если вершины vi |
и vj |
не соединены |
|
Л , |
||||
для орграфа: |
|
|
|
|
И, |
если из вершины vi |
идет дуга в вершину vj, |
||
lij = |
если из вершины vi |
нет дуги в вершину vj. |
||
Л, |
||||
Например, для графа, изображенного на рис. 5.13, в), и для орграфа, представленного на рис. 5.12, матрицы смежностей имеют соответственно вид:
|
|
Л И И Л |
|
|
|
|
Л И И И |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И Л Л И |
|
и |
|
|
Л Л И Л |
|||||||||||
|
|
L1 = |
И Л |
Л |
И |
|
|
L2 = |
|
Л |
Л |
Л |
Л |
. |
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Л И И Л |
|
|
|
|
Л Л И Л |
|||||||||||
|
|
При перемножении таких матриц смежностей умножение элементов |
||||||||||||||||
матрицы понимается как конъюнкция, а сложение – как дизъюнкция. |
||||||||||||||||||
|
|
По введенной матрице смежности или её степеням, как и в предыдущем |
||||||||||||||||
v1 |
|
|
|
v2 |
|
|
параграфе, |
можно |
|
|
определять |
наличие или |
||||||
|
|
|
|
|
отсутствие цепей (путей) заданной длины. |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
Например, по матрице Lk |
= L L … L (здесь |
||||||||||
|
|
|
|
|
|
|
содержится k множителей L) можно определить |
|||||||||||
|
|
|
|
|
|
|
наличие или отсутствие цепей (путей) длины k. |
|||||||||||
|
|
|
|
|
|
|
|
Матрица |
|
L* = L L2 L3 … Ln |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
v4 |
|
v3 |
|
|
орграфа G с n вершинами содержит все сведения |
||||||||||||
|
|
|
|
о путях любой длины между вершинами |
||||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
Рис. 5.14 |
|
|
|
заданного |
орграфа |
|
G. |
Матрица |
|
L* считается |
||||||
|
|
|
|
|
матрицей достижимости орграфа G. |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
Вычислим матрицу достижимости орграфа, представленного на рис. |
||||||||||||||||
5.14 (пример взят из [17]). Матрица смежности L и матрицы L2, L3 и L4 равны |
||||||||||||||||||
соответственно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Л И Л Л |
|
|
|
Л И Л Л |
Л И Л Л |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Л Л И И |
|
2 |
Л Л И И Л Л И И |
||||||||||||||
L = |
|
Л Л Л Л |
. |
L |
= |
Л Л Л Л |
& |
Л Л Л Л |
= |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Л Л И Л |
|
|
|
Л Л И Л |
Л Л И Л |
||||||||||||
Л |
Л |
И |
И |
|
||
|
|
|
|
|
|
|
Л |
Л |
И |
Л |
|
||
= |
Л |
Л |
Л |
Л |
|
; |
|
|
|
||||
|
|
|
|
|
||
|
|
Л |
Л |
|
|
|
Л |
Л |
|
||||
|
Л |
Л |
И |
Л |
|
||
|
|
|
|
|
|
|
|
3 |
Л |
Л |
Л |
Л |
; |
||
L = |
Л |
Л |
Л |
Л |
|
||
|
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
Л |
Л |
|
|
|
|
Л |
Л |
|
||||
|
Л |
Л |
Л |
Л |
||
|
|
|
|
|
|
|
4 |
Л |
Л |
Л |
Л |
||
L = |
Л |
Л |
Л |
Л |
. |
|
|
|
|
||||
|
|
|
|
|
||
|
|
|
Л |
Л |
|
|
|
Л |
Л |
||||

136
Следовательно, матрица достижимости равна:
|
|
Л И Л Л |
|
|
Л Л И И |
|
Л Л И Л |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
Л Л И И |
Л Л И Л |
|
Л Л Л Л |
|
|||||||||
L |
|
= |
Л Л Л Л |
|
|
Л Л Л Л |
|
|
|
Л Л Л Л |
|
= |
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Л Л И Л |
|
|
Л Л Л Л |
|
Л Л Л Л |
|
|
||||||
|
|
Л |
И |
И |
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Л |
Л |
И |
И |
|
|
|
|
|
|
|
|
||
|
= |
Л |
Л |
Л |
Л |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Л |
И |
Л |
|
|
|
|
|
|
|
|
|
|
|
Л |
|
|
|
|
|
|
|
|
|
||||
|
|
|
По матрице L* видно, что из вершины v1 достижимы вершины v2, v3 и |
||||||||||||
v4; |
из вершины v2 |
- |
вершины v3 и v4; |
из вершины v3 |
ни одна вершина |
||||||||||
недостижима, а из вершины v4 достижима только вершина v3.
Пусть G = (V,X) – орграф с n вершинами v1, v2,…,vn и его матрица смежности есть некоторая матрица L. При больших значениях числа n вычисление степеней матрицы L лучше осуществлять на ЭВМ. Для этого существует алгоритм Уоршелла. Этот алгоритм генерирует последовательность матриц W0 = L, W1, W2,…,Wn, причём элемент матрицы Wk (k≥ 1), стоящий на пересечении i–й строки и j–го столбца wk(i,j), равен И в том и только в том случае, когда существует путь (произвольной длины) из вершины vi в вершину vj с внутренними вершинами из множества {v1, v2,…,vn}. Матрица Wn является искомой матрицей достижимости исходного графа: L* = Wn.
Алгоритм Уоршелла: begin
W:= L;
for k=1 to n do
for i=1 to n do
for j=1 to n do
w(i,j)= w(i,j) или (w(i,k) и w(k,j));
end
Мы часто ищем сложности вещей, Где истина лежит совсем простая.
С. Щипачев
§ 8. Критерий изоморфизма графов
Теорема 5.8 (критерий изоморфизма графов). Графы G=(V,X) и G′=(V′,X′) с матрицами смежностей (aij) и (aij′) соответственно изоморфны тогда и только тогда, когда: 1) число вершин в V и V′ совпадает (и равны,

137
например, n); 2) существует такое взаимно однозначное соответствие ψ множества {1,2,…,n} на себя, что aij=а′ψ(i) ψ(j).
Доказательство. Необходимость. Пусть ϕ - изоморфизм G и G′. Докажем, что выполняются условия 1) и 2). Если ϕ - изоморфизм, то это означает, что ϕ взаимно однозначное отображение V на V′, следовательно, условие 1) выполняется. Отображение ϕ сохраняет смежность, поэтому если vi было соединено ребром с vj, т.е. aij=1, то ϕ(vi)=v′k будет соединено ребром с ϕ(vj)= v′m, следовательно, а′km=1. Тогда если aij=0, то а′km=0. Таким образом, ϕ порождает взаимно однозначное отображение ψ множества {1,2,…,n} на себя (ψ(i)=k, ψ(j)=m), при котором aij=а′ψ(i) ψ(j), следовательно, условие 2) выполнено.
Достаточность. Пусть выполняются условия 1) и 2). Докажем, что графы G и G′ изоморфны. Определим отображение ϕ: ϕ(vi)=v′ψ(i). Это отображение ϕ взаимно однозначное и сохраняет смежность, следовательно, ϕ - изоморфизм G и G′, что и требовалось доказать.
Доказательство теоремы с незначительными усложнениями переносится на случай мультиграфов и орграфов.
Количество взаимно однозначных отображений множества {1,2,…,n} на себя равно числу перестановок, т.е. равно n! и это число является большим при больших значениях n. Поэтому использовать непосредственно теорему 5.8 при практическом распознавании изоморфизма для графов с большим n нецелесообразно.
В большинстве случаев можно использовать следующий метод распознавания изоморфизма, который сводит перебор к минимуму. Этот метод основан на построении графа соответствия для данных графов G и G′. Рассмотрим построение графа соответствия для орграфов.
Очевидно, что если графы G и G′ изоморфны, то у соответствующих вершин одинаковы локальные степени. Для орграфов одинаковы полустепени исхода и захода соответствующих вершин. В связи с этим строим граф соответствия как граф, множество вершин которого есть V V′, и вершина из V соединена с вершиной из V′ тогда и только тогда, когда у этих вершин совпадают локальные степени (полустепени исхода и захода) в графах G и G′ соответственно. Вершины из V между собой не соединяем, вершины из V′ - тоже.
Из построенного графа соответствия определяем, какие варианты отображений вершин из V на V′ допустимы и какие нет. Эти
оставшиеся допустимые варианты придется перебрать и выяснить существование изоморфизма.
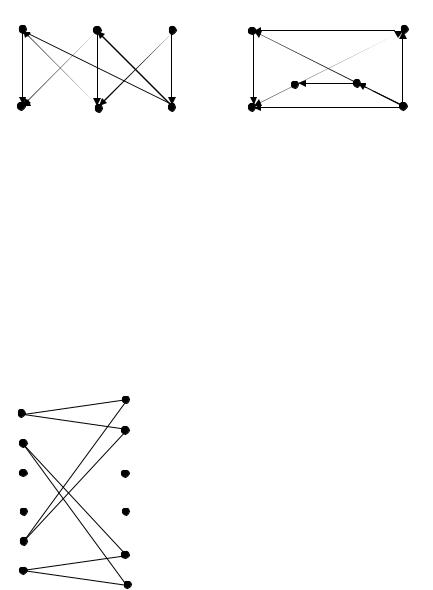
Поясним на примере. Пусть даны орграфы, изображенные на рис 5.15.
138
v1 |
v2 |
v3 |
u1 |
u2 |
|
|
|
u5 |
u6 |
v4 |
v5 |
v6 |
u4 |
u3 |
|
|
|
Рис. 5.15
В каждом графе по 6 вершин, следовательно, возможных взаимно однозначных отображений 6!=720. Перебрать все 720 отображений и выяснить среди них существование изоморфных отображений дело громоздкое.
Построим граф соответствия, см. рис. 5.16. У каждой вершины записываем полустепени исхода и захода в виде (k,l), здесь k - полустепень исхода, l - полустепень захода вершины.
|
|
|
|
|
|
vi |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
u1 |
(1,2) |
|
|||||||
|
|
|
|
↓ |
||||||||
(1,2) |
v1 |
|
1) |
|
|
|
|
|
; |
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
u2 |
(1,2) |
|
ui |
2 |
5 |
3 |
4 |
1 |
6 |
|
|
|
|
|||||||||
(2,1) |
v2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
(3,0) |
v3 |
|
u3 |
(3,0) |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
||||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
2) |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
||
(0,3) |
v4 |
|
u4 |
(0,3) |
|
1 |
6 |
3 |
4 |
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
(1,2) |
v5 |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
u5 |
(2,1) |
|
|
||||||||
|
|
|
3) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
; |
|
|
(2,1) |
v6 |
|
|
|
|
2 |
6 |
3 |
4 |
1 |
5 |
|
|
|
|
|
|
||||||||
|
u6 |
(2,1) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
Рис. 5.16 |
|
|
|
|||||||
|
|
|
4) |
|
|
|
|
|
. |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
5 |
3 |
4 |
2 |
6 |
|
Очевидно, что вершину v3 нужно отобразить на вершину u3 (v3→ u3), а v4→ u4. Вершина v1 может при изоморфных отображениях отображаться на u1
или u2, вершина v2 - на u5 или u6, вершина v5 - на u1 или u2, а v6 - на u5 или u6. Таким образом, из 720 возможных отображений осталось 4
отображения, при которых возможен изоморфизм. Эти отображения представлены справа от Рис. 5.15.
Выясним, есть ли среди них изоморфное отображение рассматриваемых графов. При отображении 1) имеем, что а51=1, а а’12=0, следовательно, не выполнено второе условие теоремы 5.8, поэтому отображение 1) не будет изоморфизмом рассматриваемых графов. При
