
- •Введение
- •Глава 1. Множества, отношения и функции
- •1. Задание множества
- •2. Операции над множествами
- •3. Разбиение множества. Декартово произведение
- •4. Отношения
- •5. Операции над отношениями
- •6. Функция
- •7. Отношение эквивалентности. Фактор-множество
- •8. Отношения порядка
- •9. Вопросы и темы для самопроверки
- •10. Упражнения
- •Глава 2. Алгебраические структуры
- •1. Операции и предикаты
- •2. Алгебраическая система. Алгебра. Модель
- •3. Подалгебры
- •4. Морфизмы алгебр
- •5. Алгебра с одной операцией
- •6. Группы
- •7. Алгебра с двумя операциями. Кольцо
- •8. Кольцо с единицей
- •9. Поле
- •10. Решетки
- •11. Булевы алгебры
- •12. Матроиды
- •13. Вопросы и темы для самопроверки
- •14. Упражнения
- •Глава 3. Булевы функции
- •2. Формулы
- •3. Упрощения в записях формул
- •4. Равносильность формул
- •5. Важнейшие пары равносильных формул
- •6. Зависимости между булевыми функциями
- •7. Свойства операций штрих Шеффера, стрелка Пирса и сложения по модулю два
- •8. Элементарные суммы и произведения. Конституенты нуля и единицы
- •9. Дизъюнктивные и конъюнктивные нормальные формы
- •10. Представление произвольной булевой функции в виде формул
- •11. Совершенные нормальные формы
- •12. Полином Жегалкина
- •13. Сокращенные дизъюнктивные нормальные формы
- •14. Метод Квайна получения сокращенной д.н.ф.
- •15. Тупиковые и минимальные д.н.ф.
- •16. Метод импликантных матриц
- •17. Минимальные конъюнктивные нормальные формы
- •18. Полнота системы функций. Теорема Поста
- •21. Функциональная декомпозиция
- •22. Вопросы и темы для самопроверки
- •23. Упражнения
- •Глава 4. Элементы комбинаторики
- •1. Правило суммы для конечных множеств
- •2. Правило произведения для конечных множеств
- •3. Выборки и упорядочения
- •5. Число всевозможных разбиений конечного множества. Полиномиальная теорема
- •6. Метод включения и исключения
- •7. Задача о беспорядках и встречах
- •8. Системы различных представителей
- •9. Вопросы и темы для самоконтроля
- •10. Упражнения по комбинаторике
- •Глава 5. Теория графов
- •1. Основные типы графов
- •2. Изоморфизм графов
- •3. Число ребер графа
- •4. Цепи, циклы, пути и контуры
- •5. Связность графа. Компоненты связности
- •6. Матрица смежности
- •7. Матрицы смежности и достижимости
- •8. Критерий изоморфизма графов
- •9. Матрица инциденций
- •10. Деревья
- •11. Задача о минимальном соединении
- •12. Центры дерева
- •13. Ориентированные деревья
- •14. Эйлеровы графы
- •15. Гамильтоновы графы
- •16. Планарные графы
- •17. Задача о кратчайшей цепи между произвольными вершинами графа
- •18. Алгоритм Дейкстры нахождения кратчайших путей от заданной вершины орграфа
- •19. Потоки в сетях
- •20. Вопросы и темы для самопроверки
- •21. Упражнения
- •Список литературы
119
Глава 5. ТЕОРИЯ ГРАФОВ
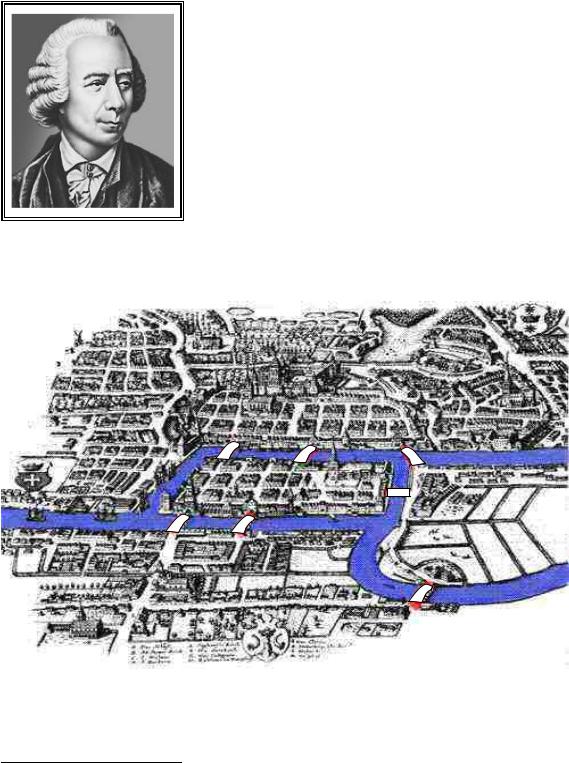
Основоположником теории графов является Эйлер (1707-1782), решивший в 1736 г. известную в то время задачу, называвшуюся проблемой кёнигсбергских мостов. Кёнигсберг (ныне Калининград) располагается на берегах реки Преголя и на двух островах, соединенных семью мостами с берегами и друг с другом, как показано на рис. 5.1. Рисунок (карта-план Мериана 1664 года) взят из [20]*, см. также [21]).
Л. Эйлер
Рис. 5.1
* Мосты выделены автором пособия белым цветом, ибо их (великолепные) изображения плохо передается при данном здесь масштабе карты.

120
Нужно выяснить, существует ли маршрут прогулки, проходящий через каждый мост один и только один раз и такой, что позволял бы, выйдя из произвольной точки города, вновь вернуться в эту же точку. Эйлер доказал, что эта задача не разрешима. Но Эйлер не стал бы Эйлером в том смысле, как мы его воспринимаем, если бы он не обобщил принципы решения этой задачи и не создал основы теории подобных задач - теории графов.
К теории графов сводятся задачи анализа электрических цепей, задачи перечисления изомеров предельных углеводородов некоторых веществ и ряд других задач.
§ 1. Основные типы графов
Графом называется совокупность, состоящая из конечного множества V точек, называемых вершинами, и множества неупорядоченных пар различных вершин из V, называемых ребрами. Множество вершин графа можно, например, положить равным: V={v1,v2,…, vn}. Множество ребер графа обозначим через X, а ребра через (vi,vj) или через xij (i,j=1,2,…,n) или через xk (k=1,2,…,m). Граф G с множеством вершин V и с множеством рёбер Х записывается как G(V,X) или G, G =(V,X).
Вершину графа изображают на рисунке (диаграмме графа) точкой, а ребро (vi,vj) графа изображают линией, соединяющей вершины vi и vj.
Пример. Пусть v1, v2, v3, v4 – вершины графа, а (v1,v2), (v1,v4), (v2,v3), (v2,v4) – рёбра, тогда диаграмма этого графа представлена на рис. 5.2. а). На рис. 5.2 б) приведены всевозможные графы с тремя вершинами, причем их вершины не помечены никакими символами и поэтому вершины не отличаются одна от другой какими-либо пометками.
v2 v3
v1 |
v4 |
а) |
б) |
Рис. 5.2
Граф называется помеченным, если его вершины отличаются одна от другой какими-либо пометками, например v1, v2,…, vn , и непомеченным, если вершины графа не различаются (не отмечены).
Каждая заданная неупорядоченная пара вершин x = (vi,vj) является ребром графа G. Считают, что x соединяет вершины vi и vj. Мы будем писать x = (vi,vj) и считать, что vi и vj – смежные вершины; вершины vi и vj
121
называются инцидентными ребру x, ребро х считается инцидентным
вершинам vi и vj.
Если два различных ребра x и y инцидентны одной и той же вершине, то они называются смежными.
Граф с n вершинами и m ребрами называется (n,m)-графом. На рис. 5.2,
б) приведены (3,0), (3,1), (3,2) и (3,3) графы. (1,0) граф называется тривиальным.
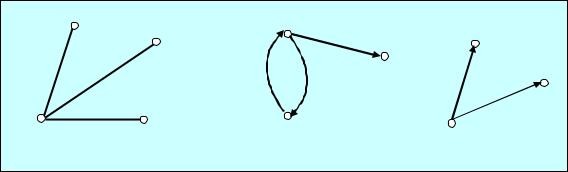
Рассмотрим (4,3) граф, изображенный на рис. 5.3, а). В этом графе вершина v1 инцидентна ребру x1, а рёбра x1 и x2 смежные ребра.
Граф, в котором вершины могут соединяться более чем одним ребром,
называется мультиграфом.
v1 |
v3 |
|
x1
x3
v4
v2 x2
а) |
б) |
в) |
|
Рис.5.3 |
|
Из определения следует, что в графе не может быть ребер, начинающихся и оканчивающихся в одной вершине, – так называемых петель. Граф, в котором есть дополнительные кратные ребра и петли,
называется псевдографом.
Орграфом или ориентированным графом называется совокупность,
состоящая из конечного множества V точек, называемых вершинами, и множества упорядоченных пар различных вершин из V, называемых дугами. Множество дуг орграфа обозначим тоже через X, а дуги как упорядоченную пару vi,vj или xij (i,j=1,2,…,n). В орграфе две вершины v и u могут быть соединены одной или двумя дугами. Дуги v,u и u,v считаются симметричными дугами. На рис. 5.3, б) приведён орграф с симметричными дугами.
Направленным орграфом считается орграф, не имеющий симметричных дуг. На Рис. 5.3, в) приведён направленный орграф.
Граф, в котором имеются и дуги, и рёбра, называется смешанным графом.
Граф G=(V,X), состоящий только из вершин, называется нуль - графом. Граф G=(V,X), в котором любые две вершины соединены ребром, называется полным. Полный граф с n вершинами обозначают через Кn.
На рис 5.4: а) - нуль – граф, б) – ориентированный граф (орграф); в) – смешанный граф, г) – полный (неориентированный) граф – граф К3.

122
Физическое содержание информации, содержащейся в графах, может быть самым разнообразным. Если вершины обозначают города, то ребра (дуги) могут представлять собой дорожную сеть между ними или линии газопроводов, или линии электропередачи, если вершины – спортивные команды, ребра (дуги) могут свидетельствовать о недельном плане игр между командами и т. д.
|
|
|
|
а) |
б) |
в) |
г) |
|
|
Рис. 5.4. |
|
Подграфом графа (орграфа) G=(V,X) называется граф (орграф) G = (V′,X′ ), множество вершин V′ которого является подмножеством вершин V графа G, а ребрами (дугами) - часть ребер (дуг) графа G, оба конца которых лежат в множестве V′.
Остовным подграфом графа G=(V,X) называется граф G=(V,X*), X* X, содержащий все вершины графа G=(V,X), но возможно не содержащий
некоторых ребер из X. |
|
|
|
|
||||
|
|
Дополнением графа (орграфа) G=(V,X) |
называется граф (орграф) |
|||||
|
|
= ( V , |
|
|
|
|
|
|
|
G |
X |
) с тем же |
множеством вершин V, а |
X является дополнением |
|||
множества Х до множества всех неупорядоченных (упорядоченных) пар вершин из V. Таким образом, в дополнении графа G вершины смежны тогда и только тогда, когда они не смежны в G.
Удаление вершины vi из графа G приводит к подграфу G\vi, содержащему все вершины графа G, за исключением vi , и все ребра графа G, не инцидентные vi. Другими словами, G\vi есть максимальный подграф графа G, не содержащий vi. Удаление ребра xj из G приводит к остовному подграфу, содержащему все ребра графа G, за исключением xj, т.е. G\xj есть максимальный подграф графа G, не содержащий xj, см рис. 5.5.
|
vi |
G\vi |
|
xj |
G\ xj |
G |
|
G |
|||
|
|
||||
|
|
|
|
Рис. 5.5. Графы, содержащие и не содержащие вершину или ребро
123
Объединением графов G1=(V1,X1) и G2=(V2,X2) называется граф,
множеством вершин которого является V=V1 V2, а множеством рёбер является X=X1 X2. Граф G=(V,X) называется двудольным, если существует разбиение множества его вершин на два непересекающихся подмножества V1 и V2 так, что V=V1 V2 и каждое ребро графа G соединяет вершины из разных множеств.
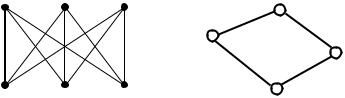
Двудольный граф называется полным двудольным графом, если любая вершина из V1 соединена ребром с каждой вершиной из V2, следовательно, каждая вершина из V2 соединена ребром с каждой вершиной из V1. Если |V1|=m и |V2|=n, то полный двудольный граф обозначается через Km,n. На рис. 5.6, а) приведён пример полного двудольного графа K3,3.
|
v2 |
S(v1)={v2, v4}; |
|
v3 |
|
v1 |
S(v2)={v1, v3, v4}; |
|
|
S(v3)={v2, v4}; |
|
|
|
|
|
v4 |
S(v4)={v1, v2, v3}. |
|
а) |
б) |
|
Рис. 5.6 |
Многие графы являются разреженными, т.е. число их ребер много меньше максимально возможного числа рёбер. В этом случае лучше задать граф с помощью списков смежностей вершин. При задании списков смежностей вершин для каждой вершины v V графа G=(V,X) выписывается множество S(v) (S(v) V) вершин, смежных с v, см. рис. 5.6, б). Размер этого представления зависит от суммы длин списков. Каждое ребро вносит вершину в два списка, поэтому сумма длин списков содержит 2 X элементов. Недостатком задания графов с помощью списков смежностей вершин является выяснение, соединены ли заданные вершины v и u ребром, ибо приходится просматривать весь список S(v) в поисках u. В случае, когда число ребер графа сравнимо с n2 (n = V ) удобнее задавать граф матрицей смежности, которая будет введена в дальнейшем.
Обобщением понятия графа является гиперграф Н(V,X), когда задается множество V вершин и множество X «ребер», которые являются некоторыми подмножествами множества V, эти подмножества могут содержать произвольное число элементов из V. Для графа ребра задаются двумя и только двумя вершинами, а в гиперграфе – произвольным числом элементов из V. Пусть, например, задано множество, состоящее из девяти вершин
V={v1, v2,…, v9} и шести «ребер»: Х = {х1, х2,…, х6}, где х1 = {v1, v4, v6}, х2 = {v1, v2, v3, v5}, х3 = {v2, v5}, х4 = {v6, v8}, х5 = {v5, v7, v8}, х6 = {v9}. В результате получили гиперграф Н(V,X), изображенный на рис. 5.7, а).
