
- •Следящая система (схема д 1111).
- •1. Введение.
- •Расчет сау в линейном приближении.
- •2.1 Вывод уравнений и определение передаточных функций функциональных элементов.
- •2.1.1 Генератор постоянного тока.
- •2.1.2 Определение параметров электромашинного усилителя
- •2.1.3 Определение параметров двигателя постоянного тока
- •2.1.4 Определение параметров делителя напряжения.
- •2.2 Структурная схема сау.
- •2.3 Передаточные функции разомкнутой и замкнутой системы.
- •2.4 Определение коэффициента усиления по заданным условиям точности в установившемся режиме.
- •2.5 Исследование статических свойств замкнутой системы.
- •2.6 Исследование динамических свойств замкнутой системы с найденным коэффициентом усиления электронного усилителя.
- •2.6.1 Построение области устойчивости по коэффициенту усиления электронного усилителя.
- •2.7 Синтез непрерывного корректирующего устройства.
- •2.8 Приближенный синтез дискретного корректирующего устройства
2.7 Синтез непрерывного корректирующего устройства.
а) Построение ЛАХ в области средних частот:
Определяется
желаемая частота среза
 по заданным значениям показателей
качества переходного процесса
по заданным значениям показателей
качества переходного процесса ,
, :
:
Для
заданных показателей качества
 %,
%, с
из номограммы по стрелкам находим
с
из номограммы по стрелкам находим и, следовательно,
и, следовательно, или
или .
При этом минимально допустимые запасы
устойчивости
.
При этом минимально допустимые запасы
устойчивости дб,
дб, град; границы среднечастотного диапазона
град; границы среднечастотного диапазона ,
, или
или ,
, .
.
Полагая
 ,
, рад/с
строим асимптотическую желаемую ЛАХ в
области низких частот
рад/с
строим асимптотическую желаемую ЛАХ в
области низких частот с наклоном –40дб/дек при частоте сопряжения
с наклоном –40дб/дек при частоте сопряжения рад/с.
В области высоких частот вправо от
частоты
рад/с.
В области высоких частот вправо от
частоты желаемую ЛАХ проводим с наклоном
–60дб/дек. В результате построения
получим желаемую ЛАХ, которой соответствует
передаточная функция
желаемую ЛАХ проводим с наклоном
–60дб/дек. В результате построения
получим желаемую ЛАХ, которой соответствует
передаточная функция
 ,
,
где
 ,
, ,
, .
.
Для
проверки выполнения условий
 ,
, ,
, и
и ,
, воспользуемся вспомогательной программой,
составленной вScript-файле:
воспользуемся вспомогательной программой,
составленной вScript-файле:
Wpas=tf([123.96],[1 0])*tf([1],[0.1182 0.6455 1]);
omega=[0.01 1 1/0.3438 1/0.0001];
L1=20*log10(123.96)+20*log10(100);L2=20*log10(123.96);L3=L2-20*log10(1/0.3438);
L4=L3-60*log10(0.3438/0.0001)
L=[L1 L2 L3 L4];
semilogx(omega,L); hold on
omega1=[0.01 0.398 2.553 37.757 1/0.0001];
M1=20*log10(123.96)+20*log10(100);M2=20*log10(123.96)+20*log10(2.553);
M3=M2-40*log10(2.553/0.224);M4=M3-20*log10(37.757/2.553);
M5=M4-60*log10(10000/37.757);
M=[M1 M2 M3 M4 M5];
semilogx(omega1,M); grid on
Wgpas=tf([123.96],[1 0])*tf([0.392 1],[4.467 1])*tf([1],[1/37.757 1])*tf([1],[1/37.757 1]);
figure; margin(Wgpas); grid on
Wgs=feedback(Wgpas,1); figure; step(Wgs);grid on
Wk=Wgpas/Wpas; zpk(Wk)
Wk2=zpk([-2.551,-2.73,-2.73],[-37.78,-37.78,-0.224],14.787);
Wgpas2=Wpas*Wk2;Wgs2=feedback(Wgpas2,1); hold on; step(Wgs2,'r--');
В результате выполнения программы строятся:
асимптотические ЛАХ нескорректированной и желаемой системы (рис. 9);

точные ЛАХ и ЛФХ желаемой системы (рис. 10) с указанием запасов устойчивости
 дб/дек,
дб/дек, ;
;переходная характеристика замкнутой системы (рис. 11), у которой
 с,
с, %;
%;
На печать выводится
выражение передаточной функции
 :
:
Zero/pole/gain:
14.7871 s (s+2.551) (s^2 + 5.461s + 8.46)
------------------------------------------
s (s+37.76)^2 (s+0.2239)
а так же выражение скорректированной передаточной функции разомкнутой системы:
Zero/pole/gain:
15507.5848 (s+2.551) (s+2.73)^2
----------------------------------------------
s (s+0.224) (s+37.78)^2 (s^2 + 5.461s + 8.46)


Таким образом, получили передаточную функцию корректирующего устройства:


Данная передаточная
функция может быть упрощена путем замены
выражения
 на выражение
на выражение .
Для сравнения на рис.11 пунктирной линией
приведена переходная характеристика
системы с уже скорректированной
передаточной функцией
.
Для сравнения на рис.11 пунктирной линией
приведена переходная характеристика
системы с уже скорректированной
передаточной функцией ,
,
 ;
;
Как видим, переходные характеристики не сильно отличаются.
Для анализа свойств
замкнутой системы с передаточной
функцией коррекции
 найдем корни характеристического
уравнения замкнутой системы, построим
переходной процесс системы при начальных
отклонениях и отсутствии входного
сигнала с помощьюScript-файла:
найдем корни характеристического
уравнения замкнутой системы, построим
переходной процесс системы при начальных
отклонениях и отсутствии входного
сигнала с помощьюScript-файла:
Wspas=tf([123.96],[1 0])*tf([1],[0.1182 0.6455 1]);
% Модель разомкнутой системы в пространстве состояний
sys=ss(Wspas);
[a,b,c,d]=ssdata(sys);
% Корректирующее устройство
% Передаточная функция
Wsk2=zpk([-2.551,-2.91,-2.91],[-37.78,-37.78,-0.224],14.8);
% Модель корректирующего устройства в пространстве состояний
sysk=ss(Wsk2);
[ak,bk,ck,dk]=ssdata(sysk);
% Модель замкнутой системы
az=[a-b*dk*c b*ck;-bk*c ak];bz=[b*dk;bk];cz=[c ck*0];dz=0;
sysz=ss(az,bz,cz,dz);
eig(az)% определение корней замкнутой системы
% Построение переходного процесса по начальным условиям
initial(sysz,[0 0 1 0 0 1])
Врезультате выполнения программы вычисляются корни:
ans =
-54.2637
-8.6532 +11.4249i
-8.6532 -11.4249i
-2.4189 + 0.6063i
-2.4189 - 0.6063i
-4.8373
и строится переходной процесс по выходу системы, приведенный на рис. 12.

Время переходного
процесса можно оценить по формуле
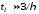 ,
где
,
где – наименьшее значение модуля вещественной
части устойчивых корней характеристического
уравнения системы. Для данного случая
– наименьшее значение модуля вещественной
части устойчивых корней характеристического
уравнения системы. Для данного случая .
При этом
.
При этом с.
с.
По передаточной
функции
 составим электрическую схему
корректирующего устройства. Для
этого сначала перепишем ее в стандартном
виде с учетом новых обозначений постоянных
времени
составим электрическую схему
корректирующего устройства. Для
этого сначала перепишем ее в стандартном
виде с учетом новых обозначений постоянных
времени :
:
 ,
,
где
 ,
, ,
,
 ,
,
 ,
,

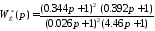

Тем самым для
реализации корректирующего устройства
необходимо использовать
интегро-дифференцирующую и дифференцирующую
цепь, разделенные усилителем с
коэффициентом усиления
 (рис. 13).
(рис. 13).

По известным
значениям постоянных времени, задаваясь
величиной электроемкостей
 мкФ,
мкФ, мкФ найдем величины:
мкФ найдем величины:
первый каскад:

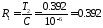 Мом,
Мом,
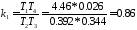 ,
,
 Мом,
Мом,
 Мом,
Мом,
 мкФ;
мкФ;
второй каскад
 Мом,
Мом,
 Мом,
Мом,
неинвертирующий операционный усилитель
Полагая
 Мом, найдем
Мом, найдем
 ,
,
 Мом.
Мом.
Учитывая, что
сопротивления
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, имеют значения порядка Мом, для
операционного усилителя будет выполнено
ограничение по току
имеют значения порядка Мом, для
операционного усилителя будет выполнено
ограничение по току
Таким образом, получившееся корректирующее звено, при включении его в систему, будет повышать качество переходного процесса.
Спроектированное звено предлагается включать в цепь усиления, то есть либо перед электронным усилителем, либо после него, либо непосредственно в электронную схему усилителя.
