2.4. Линейные однородные дифференциальные уравнения с постоянными коэффициентами

Решением дифференциального уравнения вида является фундаментальная система решений , представляемая в виде общего решения .

Решения фундаментальной системы определяется по методу Эйлера, в котором частное решение уравнения ищется в виде , гдеk = const. Тогда то

При этом многочлен называетсяхарактеристическим многочленом дифференциального уравнения, а характеристическим уравнением.

Структура фундаментальной системы уравнения зависит от вида корней характеристического уравнения. Различают три случая:

1. Все корни характеристического уравнения различны:

   1. вещественны - , тогда .

   2. имеются комплексные - ,тогда .

2. Среди корней характеристического уравнения имеются кратные:

1) - вещественный корень кратностиs, тогда

.

2) - комплексный корень кратностиs, тогда

,

где C_i –постоянные коэффициенты.

В частности для линейных однородных дифференциальных уравнений второго порядка . Еслии– корни характеристического уравнения, то общее решение записывается в одном из следующих трех видов (см. табл. 1): Таблица 1

	Корни и	Общее решение ЛОДУ
1)	действительные и различные ()
2)	действительные и равные ()
3)	комплексные (а и b – действительные числа)

Пример. Найти общее решение уравнения .

Составим характеристическое уравнение и найдем его корни: ; ; . Так как и – действительные и различные числа, то общее решение записывается в виде: .

Пример. Найти общее решение уравнения .

Характеристическое уравнение имеет вид: , , – комплексно-сопряженные корни, , . Общее решение имеет вид , отсюда .

2.5. Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами

Рассмотрим линейное неоднородное дифференциальное уравнение с произвольными коэффициентами:

Теорема. Общее решение линейного неоднородного дифференциального уравнения в некоторой области есть сумма любого его решения и общего решения соответствующего линейного однородного дифференциального уравнения.

Для решения линейного неоднородного дифференциального уравнения применяют метод вариации произвольных постоянных. Суть метода заключается в следующем: находят общее решение соответствующего однородного уравнения в виде: ; затем, полагая коэффициентыC_i функциями от х, ищется решение неоднородного уравнения: , где функции C_i(x) находятся из системы уравнений:

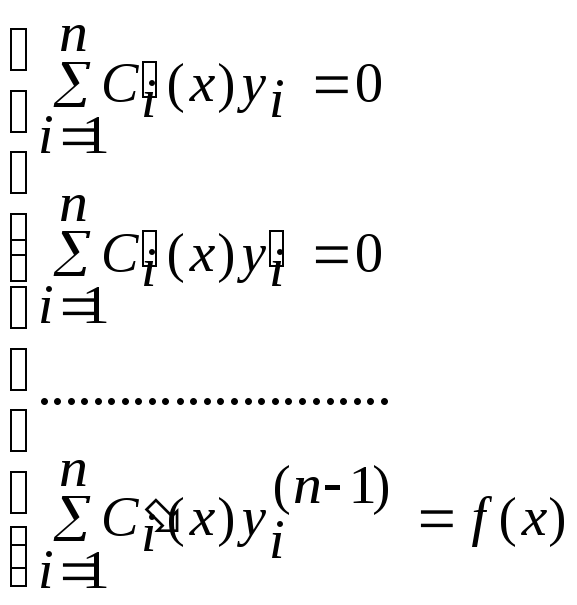
Пример. Решить уравнение

Решаем линейное однородное уравнение

.

Решение неоднородного уравнения будет иметь вид: .

Составляем систему уравнений:

Решим эту систему:

Из соотношения найдем функцию А(х).

Теперь находим В(х).

Подставляем полученные значения в формулу общего решения неоднородного уравнения:

Окончательный ответ: .

2.6. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и с правой частью специального вида

Теорема. Общее решение линейного неоднородного дифференциального уравнения равно сумме общего решения соответствующего однородного и частного решения данного неоднородного дифференциального уравнения.

Частное решение определяется методом неопределенных коэффициентов, который представлен в виде таблицы 2.

Таблица 2.

Правая часть дифференциального уравнения	Корни характеристического уравнения	Вид частного решения
	Число 0 не является корнем характеристического уравнения
	Число 0 – корень кратности r характеристического уравнения
	Число 0 не является корнем характеристического уравнения

Приложение таблицы 2.

	Число 0 – корень кратности r характеристического уравнения
	Число не является корнем характеристического уравнения
	Число – корень кратностиr характеристического уравнения
	Число не является корнем характеристического уравнения

Приложение таблицы 2.

	Число – корень кратностиr характеристического уравнения
	Число не является корнем характеристического уравнения
	Число – корень кратностиr характеристического уравнения

Пример. Решить уравнение .

Решим соответствующее однородное уравнение:

Теперь найдем частное решение исходного неоднородного уравнения.

Сопоставим правую часть уравнения с видом правой части уравнения, рассмотренного выше: Частное решение ищем в виде: , где То естьТеперь определим неизвестные коэффициенты А и В.

Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.

Итого, частное решение:

Тогда общее решение линейного неоднородного дифференциального уравнения:

Пример. Решить уравнение

Правую часть дифференциального уравнения представим в виде суммы двух функций f₁(x) + f₂(x) = x + (-sin(2x)).

Составим и решим характеристическое уравнение: .

1. Для функции f₁(x) решение ищем в виде .

Получаем: . То есть .. Итого: .

2. Для функции f₂(x) решение ищем в виде: .

Анализируя функцию f₂(x), получаем:

.

Таким образом,

. Подставляем и упрощаем:

;

Итого: то есть искомое частное решение имеет вид: . Общее решение неоднородного дифференциального уравнения: .