
Дискретизация сигналов
.pdf
Министерство образования и науки Федеральное агентство по образованию
Казанский Государственный Технический Университет им. А. Н. Туполева
Институт радиоэлектроники и телекоммуникаций
Кафедра радиоэлектронных и телекоммуникационных систем
А. А. Коробков, С. С. Седов
Методические указания к лабораторным работам по курсу «Цифровая обработка сигналов и сигнальные процессоры в системах связи
с подвижными объектами»
Казань, 2005

Дискретизация непрерывных сигналов во времени
Цель работы: исследование процессов дискретизации и восстановления непрерывных сигналов
Основные типы сигналов. Математическое описание сигналов.
Под сигналом понимают физический процесс (например, изменяющееся во времени напряжение), отображающий некоторую информацию или сообщение. Математически сигнал описывается функцией определённого типа. Используют следующие основные типы сигналов.
Одномерные сигналы описываются вещественной или комплексной функцией xa (t),
определённой на интервале вещественной оси времени t′ ≤ t ≤ t′′. |
|
Аналоговые сигналы описываются непрерывной или кусочно-непрерывной функцией xa (t), |
|
′ |
′′ |
значения и аргумент которой могут принимать любые значения на некоторых интервалах xa ≤ t ≤ xa |
|
и t′ ≤ t ≤ t′′. На рис. 1 представлен график аналогового сигнала xa (t)= Ae−αt при условиях: |
A =1, |
α > 0 , t ≥ 0 . |
|
xa(t) |
|
1 |
|
0 t
Рис. 1.
Дискретные сигналы описываются решётчатыми функциями – последовательностями x(nT ) (решётчатые функции также обозначают x(n) или xn ), где T = const - интервал дискретизации, n – целое число, n = 0,1,2,K. Функция x(nT ) может в дискретные моменты nT принимать
произвольные значения на некотором интервале. Эти значения называются отсчётами. Конечную |
||||
последовательность |
x(nT ) можно записать в следующем виде: x(nT )={x1, x2 ,..., xn }. На |
рис. 2 |
||
представлен график |
дискретной последовательности x(nT )= Ae−αnT при условиях: A =1, |
α > 0 , |
||
n = 0,1,2,.... |
|
|
x(nt) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 T |
t |
Рис. 2.
Цифровые сигналы представляют собой квантованные по уровню дискретные сигналы и могут описываться квантованными решётчатыми функциями xц (nT ), принимающие в дискретные
моменты nT лишь конечный ряд дискретных значений – уровней квантования h1, h2 ,..., hM , где М – количество уровней квантования. Решётчатая функция x(nT ) и квантованная решётчатая функция xц (nT ) связаны между собой нелинейной функцией квантования xц (nT )= Fк[x(nT )]. В радиотехнике
использую несколько видов функций квантования. В простейшем случае принимают равномерный шаг квантования ∆h = hm −hm−1 = const (рис. 3).
2

xц(nt) |
|
hN |
|
h2 |
|
h1 |
|
0 T |
t |
Рис. 3 Тогда функция квантования будет иметь вид:
h , |
x(nT )≤ |
h2 + h1 |
; |
|
|
|
|
|||||
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
hm + hm−1 |
|
hm+1 |
+ hm |
|
|
||||
xц (nT )= Fк[x(nT )]= hm , |
|
< x(nT )≤ |
; |
Каждый из уровней квантования |
||||||||
|
|
|
|
2 |
||||||||
|
|
2 |
|
|
|
|
|
|
|
|||
h , |
|
|
hM + hM −1 |
< x(nT ); |
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
M |
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
кодируется определённым числом, при этом количество уровней квантования зависит от разрядности числа. В случае использования двоичной системы исчисления количество уровней
квантования определяется как M = 2 p , где р – количество разрядов.
Дискретная дельта-функция – единичный импульс, описываемый соотношением
|
n ≠ k . |
δ(nT −kT )= 0, |
|
1, |
n = k |
|
|
Из определения дельта-функции следует, что любую последовательность x(nT ) можно записать в следующем виде:
∞
x(nT )= ∑x(kT )δ(nT −kT ).
k =−∞
Единичная последовательность описывается соотношением
|
|
n < k . |
U0 |
(nT −kT )= 0, |
|
|
1, |
n ≥ k |
|
|
|
Дельта-функции и единичная последовательность связаны между собой соотношениями:
δ(nT )=U0 (nT )−U0 (nT −T ),
∞
U0 (nT )= ∑δ(nT −kT ).
k =0
Теорема Кательникова.
Для гарантированного восстановления аналогового сигнала из дискретного, при дискретизации необходимо выполнять условие теоремы Кательникова. Согласно этой теореме, если
аналоговый сигнал xa (t) имеет ограниченный спектр, такой, что Xa (jω)= 0 при ω > ωв , то такой
сигнал можно однозначно представить последовательностью отсчётов, n = 0,1,2,.... при T = |
2π |
, где |
||
|
||||
|
|
|
ωд |
|
ωд = 2πfд > 2ωв . В этом случае аналоговый сигнал можно записать в следующем виде: |
|
|
||
xa (t)= ∑x(nT )sin[ωв(t −nT )] |
|
|
||
∞ |
|
|
|
|
n=−∞ |
ωв(t −nT ) |
. |
|
|
3
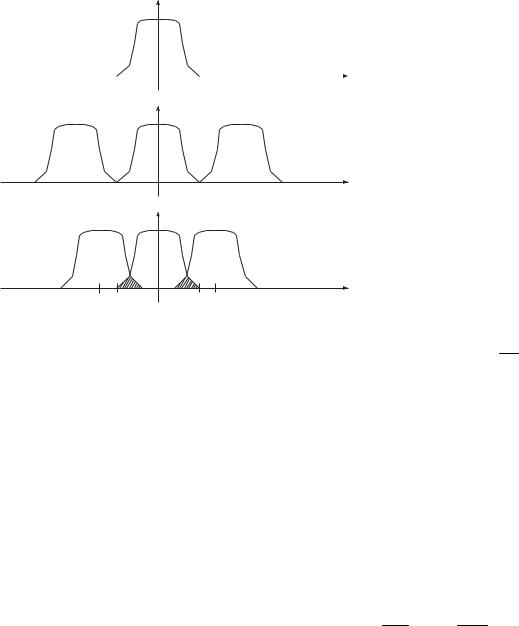
На рис. 4 представлены графики спектров сигналов при дискретизации. В случае, если не выполняется условие теоремы Кательникова, происходит наложение спектров, следствием чего
является искажения сигнала и невозможность его восстановления.
|Xа(jω)|
|
|
|
|
-ωв |
|
ω |
|
ωв |
|||
|X(ejωT)| |
ωд=2ωв |
|
|
|
|
|
|
|
|
|
ω |
-ωд |
-ωв |
ωв |
|
|||||
ωд |
||||||||
|
|
|
|
|X(ejωT)| |
|
|
ωд<2ωв |
|
|
|
|
|
|
|
|
|
|
-ωд -ωв |
ω |
ωв ωд |
Рис. 4.
Спектр дискретного сигнала и спектр аналогового сигнала при частоте дискретизации ωд = 2Tπ
связаны следующим соотношением:
|
|
X (e jωT )= |
|
1 |
∑∞ |
X a (j(ω +kωд )). |
(3) |
|
|
|
|
|
|||||
|
|
|
|
T k =−∞ |
|
|
||
Из выражения (3) следует, что спектр последовательности x(nT ) равен с точностью |
до |
|||||||
сомножителя |
1 |
сумме спектров соответствующего сигнала xa (t) |
, смещённых по оси частот на все |
|||||
T |
||||||||
|
|
|
|
|
|
|
||
возможные значения частоты, кратные частоте дискретизации.
Во многих системах связи спектр аналогового сигнала X a (jω) не содержит нулевую частоту и сосредоточен в некоторой области от ωн ≠ 0 до ωв . При выполнении теоремы Кательникова в этом
случае частота дискретизации оказывается завышенной, что приводит к увеличению избыточности, объёма информации и, соответственно, к увеличению времени передачи. В этом случае частоту
дискретизации целесообразно выбирать исходя из следующего соотношения: 2ωq в ≤ωд ≤ q2ω−н1 , где
|
ω |
в |
|
q =1,2,...int |
|
. |
ωв −ωн
Описание лабораторной установки
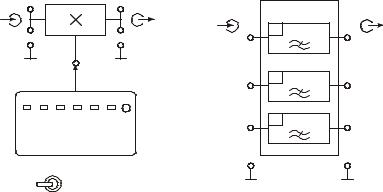
Исследуемое устройство размещено на сменном блоке «ТЕОРЕМА КОТЕЛЬНИКОВА» (рис. 4). Оно представляет собой дискретизатор, обозначенный на макете как перемножитель сигналов «Х» и набор из трех фильтров нижних частот - восстановителей сигнала с разными частотами среза Fср (3 кГц, 6 кГц и 12 кГц). Источники исследуемых сигналов - s1, s2, s3 находятся в блоке «ИСТОЧНИКИ СИГНАЛОВ», а сами сигналы представляют собой сумму гармоник с частотами 2 кГц, 4 кГц и 6 кГц.
4
ДИСКРЕТИЗАЦИЯ СИГНАЛОВ Теорема Котельникова
Uвх |
|
|
|
Uвых |
|
ФНЧ |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Fср=3кГц |
|
|
|
Uд |
|
2 |
Fср=6кГц |
|
|
|
|
|
||
3 |
6 |
12 |
16 24 |
48 |
|
|
|
|
Fд (кГц) |
|
3 |
Fср=12 |
|
Генератор импульсов |
|
|
||||
|
дискретизации |
|
|
|||
Рис. 4. Лицевая панель лабораторной установки
Дискретизатор формирует отсчеты s(k∆t) непрерывного сигнала s(t) путем перемножения этого сигнала на короткие импульсы дискретизации (Uд). Временной интервал между соседними отсчетами дискретизированного сигнала s(k∆t) зависит от выбора частоты дискретизации fд: ∆t=1/fд Эта частота меняется дискретно нажатием кнопки «fд», при этом выбранное значение частоты fд индицируется светодиодом (fд 3; 6; 12; 16; 24; и 48 кГц). Частоты дискретизации жестко
синхронизированы с частотами гармоник исследуемых сигналов, что упрощает наблюдение процессов на осциллографе.
В качестве фильтров используются три активных ФНЧ 4 порядка. Для снятия импульсных характеристик фильтров используется генератор коротких импульсов «дельта-функции» - гнездо «δ(t)» в блоке «ИСТОЧНИКИ СИГНАЛОВ».
Согласно т. Котельникова, отсчеты, следующие через интервал времени ∆t<=1/2Fв, где Fв - верхняя частота спектра сигнала, могут быть преобразованы в исходный сигнал s(t) после прохождения через идеальный ФНЧ с частотой среза Fср=Fв. В работе используются реальные ФНЧ с достаточно крутыми спадами АЧХ после частоты среза, но, тем не менее, не вертикальными. Поэтому на практике ∆t следует выбирать несколько меньше, чем по т. Котельникова.
В качестве измерительных приборов в работе используются двухлучевой осциллограф и компьютер в режиме анализатора спектра.
Порядок выполнения лабораторной работы
1. Дискретизация сигнала.
1.1.Выбрать один из трех сигналов (например s1) и подать его на вход «А» компьютера, работающего в режиме спектроанализатора. Входы компьютера находятся в нижней части стенда справа.
1.2.С помощью спектроанализатора получить спектр сигнала, нарисовать его график и определить верхнюю частоту Fв.
1.3.Рассчитать требуемую частоту дискретизации fд и установить ее на макете кнопкой «fд».
1.4.Соединить входы двухлучевого осциллографа со входом и выходом дискретизатора, установить режим внешней синхронизации осциллографа (от гнезда С2 блока «ИСТОЧНИКИ СИГНАЛОВ»). Вход спектроанализатора подключить к выходу дискретизатора.
1.5.Нарисовать графики следующих сигналов (с сохранением масштаба по времени !).
-исследуемый входной сигнал s(t);
-импульсы дискретизации (гнездо нижнего входа перемножителя);
-выходной дискретизированный сигнал s(k∆t).
1.6.Переключая кнопкой частоту fд на 1-2 шага выше и ниже выбранного значения в п. 1.3, наблюдать изменения в осциллограмме и спектре на выходе дискретизатора. Наиболее характерные случаи зафиксировать в отчете!
2. Исследование фильтров.
5
2.1.Из трех ФНЧ выбрать наиболее подходящий для восстановления исходного сигнала. Для
этого определить частоту среза Fср по АЧХ либо по импульсной характеристике g(t). Кроме того, АЧХ нужна для для последующей коррекции fд, а импульсная характеристика g(t) - для объяснения процесса восстановления сигнала.
2.2.Для снятия АЧХ фильтра подать на его вход гармонический сигнал напряжением 1 В и частотой 1 кГц от генератора в блоке «ИСТОЧНИКИ СИГНАЛОВ». К выходу фильтра подключить встроенный цифровой вольтметр. Плавно увеличивая частоту генератора, снять частотную
характеристику Uвых=ϕ(f) с шагом 0.5-1 кГц и зафиксировать частоту среза Fср, на которой Uвых |
||
окажется в |
2 раз меньше, чем на частоте 1 кГц., |
а также зафиксировать частоты, где Uвых |
уменьшится до 0.1 и 0.05 от Uвых(1 кГц). |
|
|
Построить на одном графике АЧХ трех фильтров и отметить на них уточненные значения |
||
частот среза Fср. Выбрать лучший фильтр - восстановитель исходного сигнала. |
||
2.3 Снятие импульсной характеристики фильтра g(t) производится путем подачи на его вход |
||
коротких импульсов от гнезда «δ(t)» в блоке «ИСТОЧНИКИ СИГНАЛОВ». Осциллограмма сигнала |
||
с выхода фильтра будет соответствовать при этом g(t). Построить графики g(t) для трех фильтров, |
||
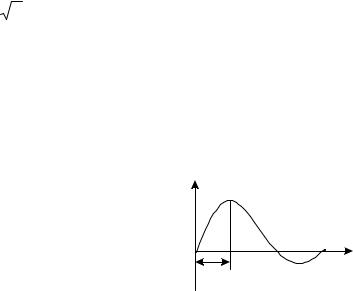
фиксируя на них значения «нулей» (когда g(t)=0). Найти интервал времени ∆t’, как показано на |
||
рисунке 5, и записать его для трех фильтров. По ∆t’ найти частоты среза фильтров: Fср=1/2∆t’. |
||
|
g(t) |
|
|
0 |
t |
|
∆t’ |
|
|
|
|
|
Рис.5 Импульсная характеристика ФНЧ |
|
2.4. По пунктам 2.2 и 2.3 выбрать фильтр, наиболее пригодный для восстановления |
||
дискретизированного сигнала. |
|
|
3. Восстановление дискретизированного сигнала. |
|
|
3.1.Сопоставляя спектры, снятые по п. 1.2 и 1.6. с АЧХ выбранного фильтра, скорректировать частоту дискретизации, увеличив ее на 1-2 шага от расчетного значения.
3.2.Соединить выход дискретизатора с входом выбранного ФНЧ, установить на макете
выбранное в п. 3.1. значение fд. Подключить один из входов осциллографа к входу дискретизатора, а второй - к выходу ФНЧ, зафиксировать в отчете осциллограммы исходного и восстановленного сигнала.
3.3.Изменяя кнопкой частоту fд, на 1-2 шага выше и ниже скорректированного значения, зафиксировать наиболее характерные осциллограммы восстановленных сигналов. В отчете сделать
заключение о том, допустимо ли изменять интервал ∆t между отсчетами дискретизированного сигнала.
Отчет должен содержать:
Функциональную схему установки. Осциллограммы, спектры и характеристики фильтров по всем пунктам задания. Вывод по пункту 3.3.
Контрольные вопросы
1.Каков практический смысл в дискретизации сигналов?
2.В чем заключается теорема Котельникова?
3.Каким нужно выбрать интервал дискретизации, чтобы сигнал был восстановлен после дискретизации без искажений?
4.Какую функцию выполняет ФНЧ?
5.В чем отличие реального и идеального ФНЧ?
6.С какой целью в работе исследовались спектры входного и дискретизированного сигналов?
7.Почему при восстановлении дискретизированных сигналов могут возникнуть искажения?
Литература 1. Гольденберг Л. М. и др. Цифровая обработка сигналов: Учеб. Пособие для вузов. - М.:
Радио и связь, 1990.
6
