
- •§1. Обыкновенные дифференциальные уравнения
- •1. 1. Основные понятия дифференциальных уравнений
- •1.2. Геометрическая интерпретация решений дифференциальных уравнений
- •1.3. Уравнения с разделяющимися переменными
- •1.4. Однородные уравнения
- •1.5. Уравнения, приводящиеся к однородным
- •Разделяем переменные:
- •1.6. Линейные неоднородные дифференциальные уравнения
- •Подставляем полученное равенство в исходное уравнение:
- •1.7. Уравнение Бернулли
- •1.8. Уравнения в полных дифференциалах
- •1.9. Уравнения первого порядка не разрешенные относительно производной
- •2. Уравнения Лагранжа и Клеро.
- •§2. Дифференциальные уравнения высших порядков
- •2.1 Основные понятия
- •2.2. Уравнения, допускающие понижение порядка
- •2) Уравнения, не содержащие явно искомой функции и ее производных до порядка k – 1 включительно.
- •3) Уравнения, не содержащие явно независимой переменной.
- •2.3. Линейные дифференциальные уравнения высших порядков
- •2.4. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •2.5. Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами
- •2.6. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и с правой частью специального вида
- •§3. Нормальные системы линейных однородных дифференциальных уравнений с постоянными коэффициентами
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Уравнения не разрешенные относительно производной
1.3. Уравнения с разделяющимися переменными
Дифференциальное
уравнение
![]() называетсяуравнением
с разделяющимися переменными,
если его можно записать в виде:
называетсяуравнением
с разделяющимися переменными,
если его можно записать в виде:
![]() .
.
Общее
решение дифференциального уравнения
с разделяющимися переменными
получается после нахождения соответствующих
интегралов, то есть
![]() .
.
Если
уравнение с разделяющимися переменными
имеет вид:
![]() ,
то путем почленного деления его на
,
то путем почленного деления его на![]() они сводится к уравнению
они сводится к уравнению![]() .
.
Замечания.
При проведении почленного деления ДУ на
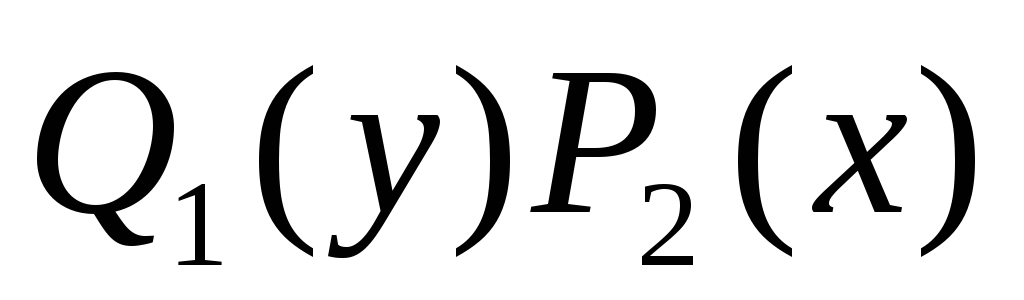 могут быть потеряны некоторые решения.
Поэтому следует отдельно решить
уравнение
могут быть потеряны некоторые решения.
Поэтому следует отдельно решить
уравнение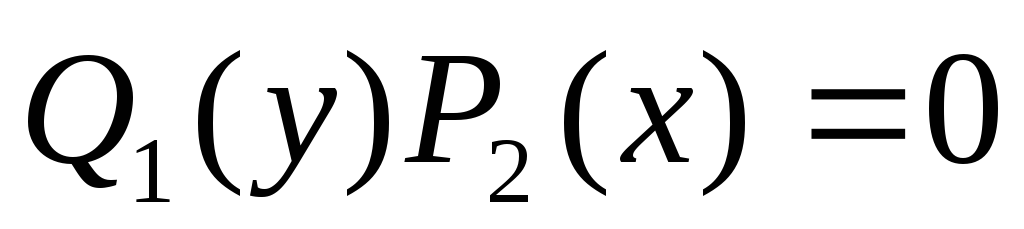 и установить те решения ДУ, которые не
могут быть получены из общего решения,
-особые
решения.
и установить те решения ДУ, которые не
могут быть получены из общего решения,
-особые
решения.Уравнение
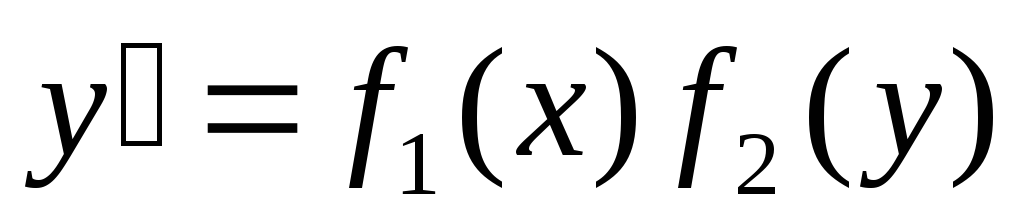 также сводится к уравнению с разделенными
переменными. Для этого достаточно
положить
также сводится к уравнению с разделенными
переменными. Для этого достаточно
положить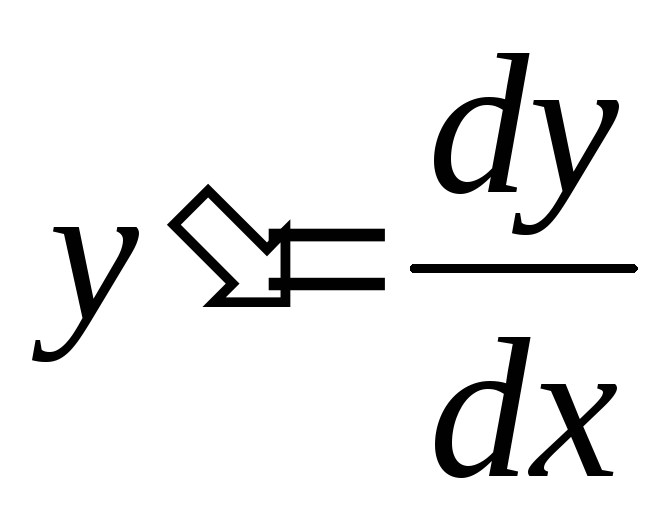 и разделить переменные:
и разделить переменные: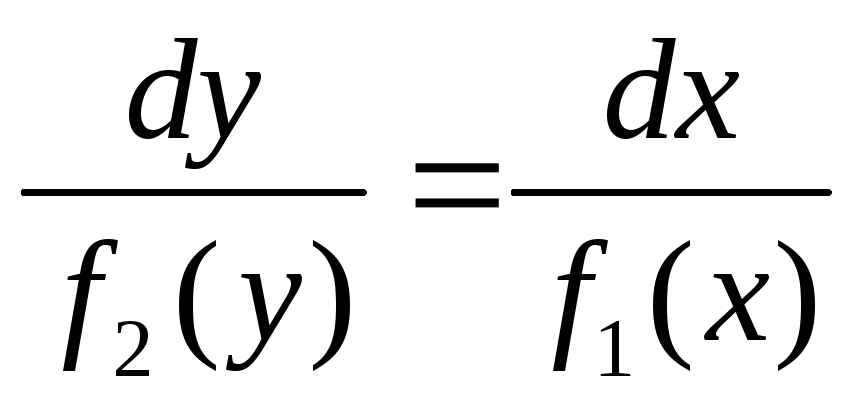 .
.Уравнение
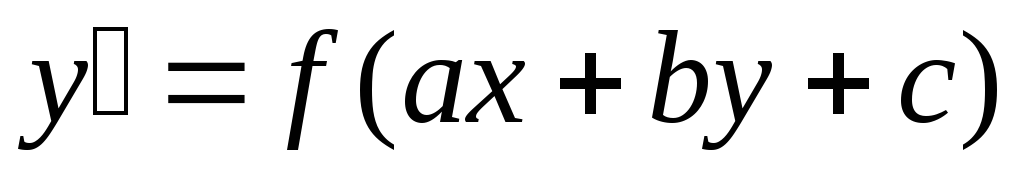 ,
гдеa,b,c
– числа, сводится к уравнению с
разделенными переменными путем замены
,
гдеa,b,c
– числа, сводится к уравнению с
разделенными переменными путем замены
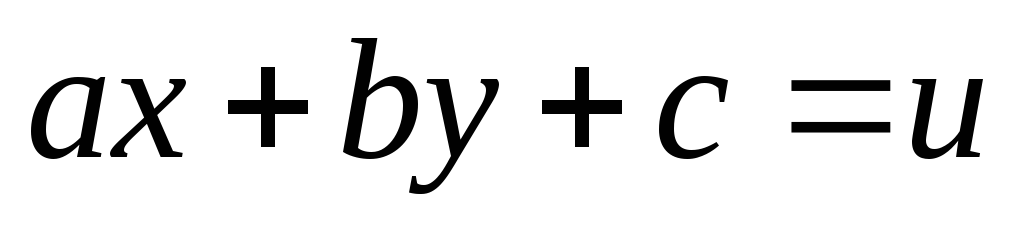 .
Дифференцируя
.
Дифференцируя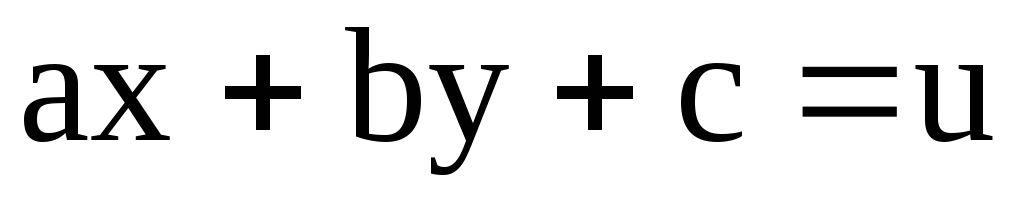 пох
получаем:
пох
получаем:
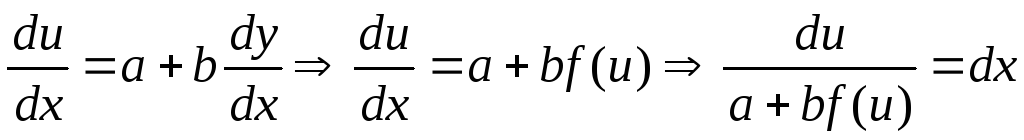 .
Интегрируя это уравнение и заменяяu=
.
Интегрируя это уравнение и заменяяu=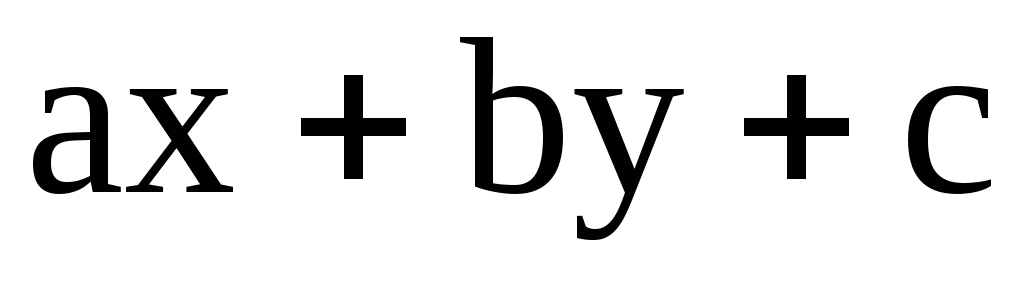 ,
получим общий интеграл исходного
уравнения.
,
получим общий интеграл исходного
уравнения.
Пример.
Найти все решения уравнения
![]() .
.
Разделяем
переменные:
![]() .Интегрируем:
.Интегрируем:
![]() .
.
Получаем:
![]() или
или
![]() .
.
В полученном выражении содержатся не все
решения данного уравнения. При делении
на
полученном выражении содержатся не все
решения данного уравнения. При делении
на![]() потеряны решения
потеряны решения![]() - это особые решения, которые невозможно
включить в решение. Множество интегральных
кривых данного уравнения состоит из
семейства окружностей радиусом 1 с
центром в точке (С; 0) и прямых
- это особые решения, которые невозможно
включить в решение. Множество интегральных
кривых данного уравнения состоит из
семейства окружностей радиусом 1 с
центром в точке (С; 0) и прямых![]() .
.
Рис. 2
1.4. Однородные уравнения
Однородной
функцией f(x,
y)
нулевого измерения, или, просто, однородной
функцией, называется функция только от
отношения
![]() .
Однородным
дифференциальным уравнением называется
уравнение вида:
.
Однородным
дифференциальным уравнением называется
уравнение вида:
![]() .
.
При
решении однородных дифференциальных
уравнений сохраняя прежнюю независимую
переменную х,
вводят вспомогательную неизвестную
функцию t
по формуле:
![]() .
Откуда
.
Откуда![]() .
Преобразуя уравнение
.
Преобразуя уравнение![]() ,
получаем:
,
получаем:![]() .
Найдя отсюда выражение дляt
как функции от x
возвращаются к переменной
.
Найдя отсюда выражение дляt
как функции от x
возвращаются к переменной
![]() ,
получая при этом решение однородного
дифференциального уравнения.
,
получая при этом решение однородного
дифференциального уравнения.
Замечание:
Иногда
целесообразно вместо постановки
![]() использовать подстановку
использовать подстановку![]() .
.
Пример.
Решить уравнение
![]() .
.
Делаем
замену:
![]() .
.
Подставляем
в исходное уравнение:
![]()
Разделяем
переменные:
![]() .
.
Интегрируя:
![]() ,
получаем:
,
получаем:
![]()
Переходя
от вспомогательной функции обратно к
функции у, получаем общее решение:
![]()
1.5. Уравнения, приводящиеся к однородным
Дифференциальное
уравнение вида:
![]() приводится к однородному дифференциальному
уравнению или к дифференциальному
уравнению с разделяющимися переменными.
приводится к однородному дифференциальному
уравнению или к дифференциальному
уравнению с разделяющимися переменными.
1 случай. Уравнение, приводящиеся к однородному дифференциальному уравнению.
Если
определитель
![]() то совершается замена:
то совершается замена:![]() где
и
- решения системы уравнений
где
и
- решения системы уравнений
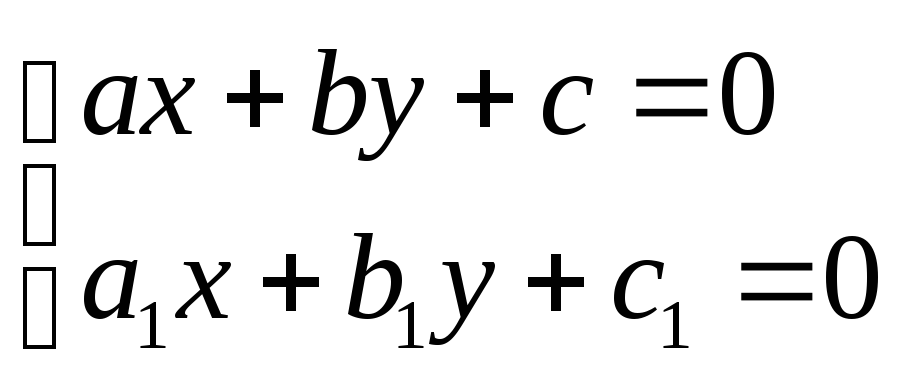 .
Подставляя замену, получим однородное
дифференциальное уравнение вида:
.
Подставляя замену, получим однородное
дифференциальное уравнение вида: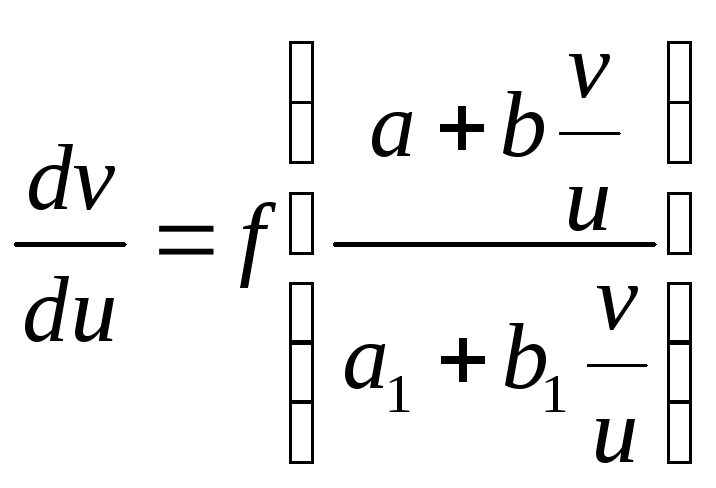 .
.
Пример.
Решить уравнение
![]()
Получаем
![]()
Находим
значение определителя
![]() .
.
Решаем
систему уравнений
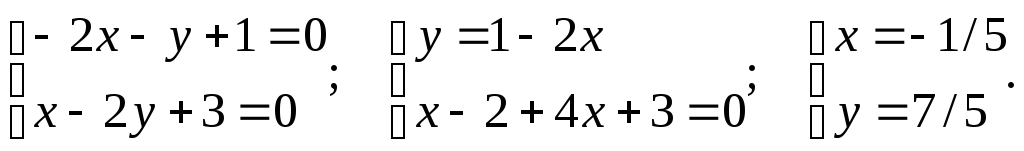
Применяем
подстановку
![]() в исходное уравнение:
в исходное уравнение:
![]()
![]()
![]()
Получили
однородное уравнение и осуществляем
замену переменных
![]() при подстановке в выражение имеем:
при подстановке в выражение имеем:
![]() .
.
Разделяем переменные:
![]()
![]() ;
;
![]() ;
;
![]() .
.
Вернемся к первоначальной функции у и переменной х.
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Получаем
выражение
![]() ,
которое является общим интегралом
исходного дифференциального уравнения.
,
которое является общим интегралом
исходного дифференциального уравнения.
2 случай. Уравнение, приводящиеся к дифференциальному уравнению с разделяющимися переменными.
Если
определитель
![]() то совершается замена:
то совершается замена:![]() ,
где
,
где![]() .
Отсюда,
.
Отсюда,![]() .
Подставляя замену, получим дифференциальное
уравнение вида:
.
Подставляя замену, получим дифференциальное
уравнение вида:![]() .
.
Пример.
Решить
уравнение
![]()
Получаем
![]()
Находим
значение определителя
![]() .
.
Применяем
подстановку
![]() ,
тогда
,
тогда
![]() .
.
Подставляем это выражение в исходное уравнение:
![]() .
.
Разделяем
переменные:
![]()
![]()
![]() .
.
Далее возвращаемся к первоначальной функции у и переменной х.
![]()
![]()
![]() –получили
общий интеграл исходного дифференциального
уравнения.
–получили
общий интеграл исходного дифференциального
уравнения.
