Тема 9 Излучение электромагнитных волн

1. Введение

Рис 27

Практически в качестве излучателей электромагнитных волн (антенн) применяют схемы, удовлетворяющие определенным требованиям. Обычно стремятся уменьшить реактивную мощность, непосредственно связанную с антенной и не излучаемую в пространство.

Один из вариантов схемы, обеспечивающей интенсивное излучение, показан на рис. 27. Эта схема, в которой пластины заменены проводами с шарами на концах, была впервые осуществлена Генрихом Герцем и известна под названием диполя Герца.

Инициатива и практическое решение вопроса применения радиоволн в качестве средства связи принадлежит А.С. Попову, который впервые в мире осуществил сеанс радиосвязи. Им же были предложены и осуществлены передающие и приемные антенны в виде несимметричных вибраторов.

2. Элементарный электрический вибратор

Элементарным электрическим вибратором (ЭЭВ) называют короткий по сравнению с длиной волны провод, обтекаемый электрическим током, амплитуда и фаза которого не изменяются вдоль провода. Этот вибратор является по существу идеализированной, удобной для анализа излучающей системой, так как практически создание вибратора с неизменными по всей длине амплитудой и фазой тока невозможно. Однако вибратор Герца (рис.27) оказывается весьма близким по своим свойствам к ЭЭВ.

Изучение поля ЭЭВ крайне важно для понимания процесса излучения электромагнитных волн антеннами. Любое проводящее тело, обтекаемое токами, можно считать как бы состоящим из множества элементарных электрических вибраторов, а при определении поля, создаваемого этими токами, можно воспользоваться принципом суперпозиции, т.е. рассматривать его как сумму полей элементарных вибраторов.

Перейдем к анализу поля ЭЭВ, расположенного в безграничной однородной изотропной среде, характеризуемой параметрами. Ток в вибраторе будем считать известным, т.е. сторонним током, изменяющимся по закону где -его амплитуда, а -начальная фаза (фаза в момент времениt = 0). Так как поле, создаваемое вибратором, в рассматриваемом случае является монохроматическим, удобно воспользоваться методом комплексных амплитуд. Вместо тока введем комплексную величину , где комплексная амплитуда стороннего тока. Токсвязан с обычным соотношением Таким образом, задача сводится к нахождению поля по заданному распределению тока. Сначала найдем векторный потенциал А. Введем сферическую систему координатполярная ось которой (осьZ) совпадает с осью вибратора, а начало координат находится в его центре (рис. 28).

Комплексная амплитуда векторного потенциала в случае мо­нохроматического поля при произвольном распределении токов в объеме V определяется формулой (2.58). Разобьем интегрирова­ние по объему, занимаемому ЭЭВ, на интегрирование по площади

Рис 28

Рис 29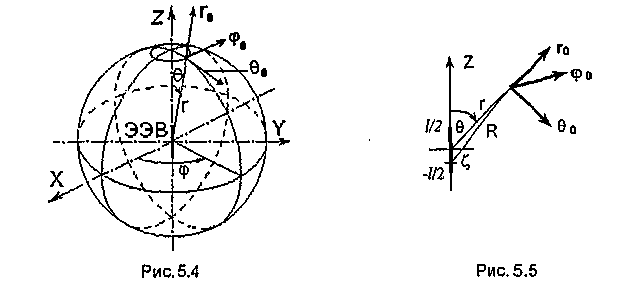

его поперечного сеченияи по длине вибратораДля упрощения преобразований будем считать поперечный размер вибратора (диаметр) малым по сравнению с его длинойУчитывая, что , запишем:

(1)

- значение координаты точки интегрирования (рис.29). При вычислении интеграла (1) ограничимся случаем, когда расстояние от вибратора до точек, в которых определяется поле, велико по сравнению с длиной вибратора Тогда в знаменателе подынтегрального выражения величину R можно считать равнойи вынести за знак интеграла. Так как то наибольшая относительная погрешность, возникающая при замене R на r, имеет порядокКроме того, по предположениюКак известно из курса физики, отношениеравно длине волныв среде без потерь с параметрамиПоэтому и в (1) можно заменитьПри такой замене погрешность определения фазы подынтегрального выражения равнаС учетом изложенного формула (1) принимает вид

Отметим, что сделанное предположение о малости диаметра вибратора d no сравнению с его длиной не является необходимым. Достаточно считать, что Векторсвязан с соотношениемОпределимиз первого уравнения Максвелла:

(2)

Так как орт лежит в плоскости, перпендикулярной оси Z, а углы между осью Z и ортами и учитывая, что все составляющие векторане зависят от переменнойполучаем, что вектор имеет только азимутальную составляющую:

Произведя дифференцирование, получим

(3)

Для определения вектора подставим найденный вектор в (2). Учитывая, чтоприходим к выражению

После дифференцирования имеем

(4)

(5)

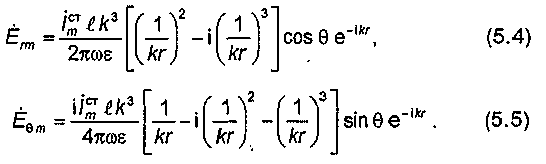
Полученные формулы определяют составляющие комплексных амплитуд векторов Е и Н.