Задачи для самостоятельного решения
1.Составить
уравнения плоскостей, параллельных
координатным плоскостям и проходящим
через точку
![]() .
.
Ответ:
![]() .
.
2.
Составить уравнение плоскости, проходящей
через линию пересечения плоскостей
![]() и
и![]() и параллельной вектору
и параллельной вектору![]() .
.
Ответ:
![]() .
.
3.
Вычислить расстояние от точки
![]() до плоскости, проходящей через точки
до плоскости, проходящей через точки![]() .
.
Ответ: d=9.
4.
Даны плоскости
![]() и
и![]() .
Какая из них ближе к началу координат?
.
Какая из них ближе к началу координат?
Ответ:
![]() .
.
5.
Две грани куба лежат соответственно
на плоскостях
![]() и
и![]() .
Вычислить объем данного куба.
.
Вычислить объем данного куба.
Ответ: 8 куб.ед.
6. Доказать, что параллелепипед, три непараллельные грани которого лежат в плоскостях
![]() ,
,
![]() ,
,
![]()
является прямоугольным.
7.
На оси ординат найти точку, отстоящую
от плоскости
![]() на расстоянии трёх единиц.
на расстоянии трёх единиц.
Ответ:
![]() ,
,![]() .
.
8.
Составить уравнение плоскости, проходящей
через точку
![]() и отсекающей равные отрезки на осях
координат.
и отсекающей равные отрезки на осях
координат.
Ответ:
![]() .
.
9.
Из точки
![]() на координатные плоскости опущены
перпендикуляры. Найти уравнение
плоскости, проходящей через их основания.
на координатные плоскости опущены
перпендикуляры. Найти уравнение
плоскости, проходящей через их основания.
Ответ:
![]() .
.
10.
Найти уравнение плоскости, точки которой
одинаково удалены от точек
![]() и
и![]() .
.
Ответ:
![]() .
.
§ 3. Прямая в пространстве
Основные теоретические сведения
1. Общее уравнение прямой:
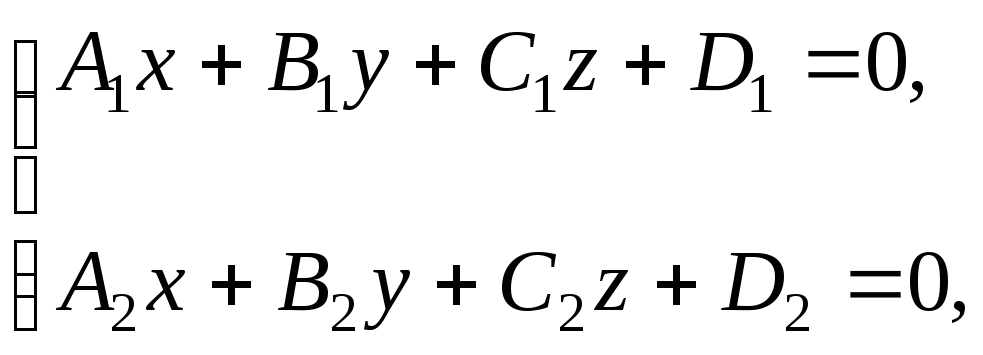 (3.1)
(3.1)
определяется как линия пересечения двух плоскостей, при условии, что они не параллельны.
Каждый не равный
нулю вектор, лежащий на данной прямой
или параллельный ей, называется
направляющим этой прямой
![]() .
Если известна одна точка
.
Если известна одна точка![]() ,
принадлежащая прямой, то прямая может
быть задана каноническими уравнениями:
,
принадлежащая прямой, то прямая может
быть задана каноническими уравнениями:![]() .
.
2. ![]() . (3.2)
. (3.2)
|
Рис. 2.19 |
3.
Параметрическими
уравнениями прямой, проходящей через
точку
|
Здесь
![]() произвольно изменяющийся параметр.
При изменении
произвольно изменяющийся параметр.
При изменении![]() величины
величины![]() меняются так, что точка
меняются так, что точка![]() движется по данной прямой.
движется по данной прямой.
4.
Канонические уравнения прямой, проходящей
через две данные точки
![]() и
и![]() имеет вид
имеет вид
![]() . (3.4)
. (3.4)
Параметрические уравнения прямой, проходящей через две данные точки
 (3.5)
(3.5)
Если
в системе (3.5) t
меняется на отрезке
![]() ,
то (3.5)определяет
отрезок прямой
,
то (3.5)определяет
отрезок прямой
![]() причем параметру
причем параметру![]() соответствует точка
соответствует точка
![]() ,
параметру
,
параметру![]() –
точка
–
точка![]() .
.
5.
Угол
![]() между двумя прямыми, заданными своими
каноническими или параметрическими
уравнениями, вычисляются по формуле
между двумя прямыми, заданными своими
каноническими или параметрическими
уравнениями, вычисляются по формуле
![]() . (3.6)
. (3.6)
6. Условие параллельности прямых
![]() (3.7)
(3.7)
Условие перпендикулярности прямых
![]() (3.8)
(3.8)
следует из условия перпендикулярности направляющих векторов.
7. Условие пересечения прямых (условие компланарности):
|
Рис. 2.20 |
Это условие (3.9) – условие компланарности прямых (рис. 2.20). Если оно не выполняется и прямые не параллельны, то данные прямые называются скрещивающимися (лежат в параллельных плоскостях). |
Примеры решения задач
Задача
3.1. Составить
уравнение прямой, образованной
пересечением плоскости
![]() с плоскостью, проходящей через осьОх
и точку
с плоскостью, проходящей через осьОх
и точку
![]() .
.
Решение.
Составим
уравнение плоскости, проходящей через
ось Ох
и точку
![]() .
Нормальный вектор этой плоскости имеет
вид
.
Нормальный вектор этой плоскости имеет
вид![]() .
Используем уравнение (3.1), получим
.
Используем уравнение (3.1), получим![]() или
или![]() .
Но так как плоскость проходит через
начало координат, то
.
Но так как плоскость проходит через
начало координат, то![]() ,
следовательно,
,
следовательно,![]() .
Тогда
.
Тогда![]() или
или![]() уравнение искомой плоскости. Прямую
запишем в общем виде (3.2)
уравнение искомой плоскости. Прямую
запишем в общем виде (3.2)
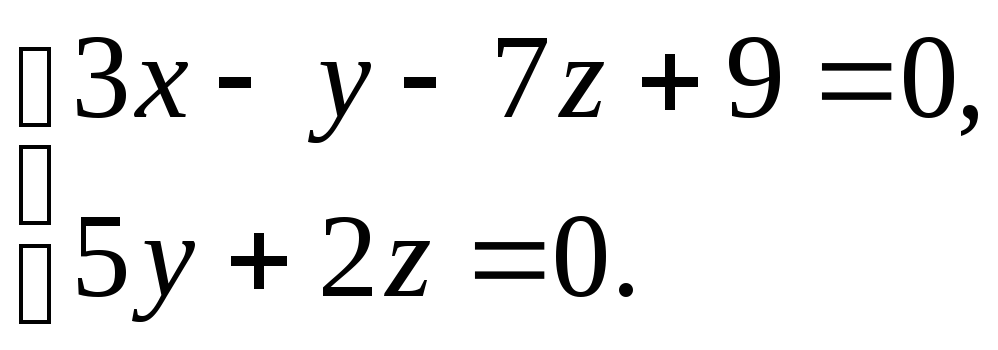
Ответ.
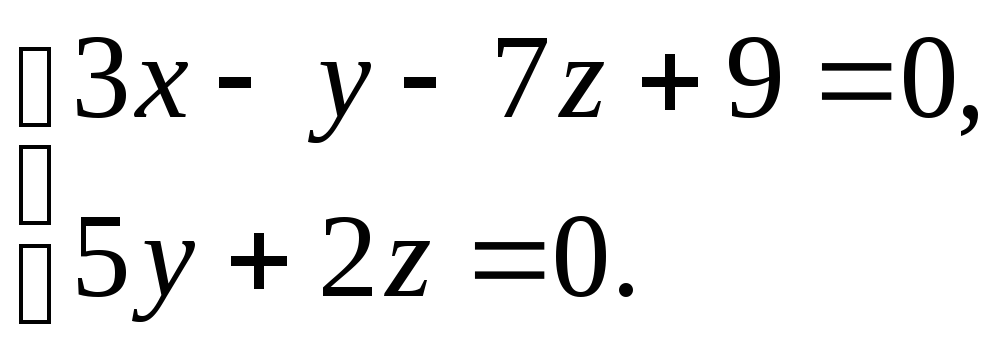
Задача
3.2. Через
точки
![]() и
и![]() проведена прямая. Определить точки
пересечения этой прямой с координатными
плоскостями.
проведена прямая. Определить точки
пересечения этой прямой с координатными
плоскостями.
Решение. Запишем уравнение прямой, проходящей через две точки в параметрической форме (3.5), получим

Найдём
пересечение этой прямой с координатной
плоскостью xOy,
которая имеет уравнение
![]() для этого решим совместно уравнения
прямой и плоскости
для этого решим совместно уравнения
прямой и плоскости

Отсюда
![]() ,
следовательно,
,
следовательно,![]() ,
тогда
,
тогда
![]() ,
,
т.е. точка (9;-4;0) является точкой пересечения прямой и плоскости xОy.
Решая две системы
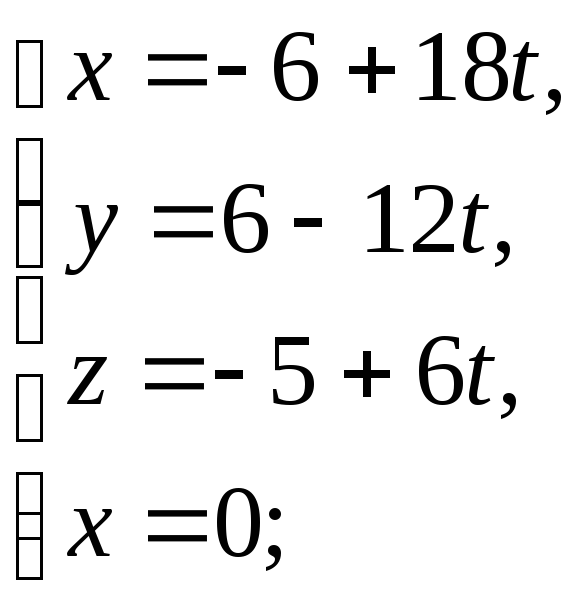 и
и 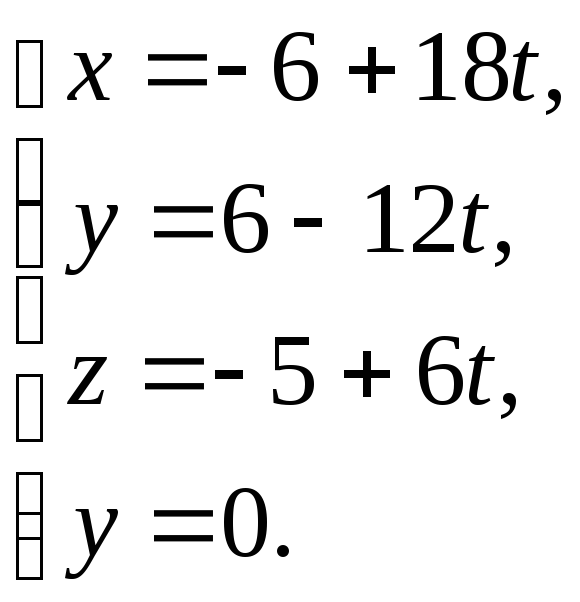
Найдём точки пересечения прямой с плоскостями yОz и zОy –точки (0,2,-3) и (3,0,–2) соответственно.
Ответ: (9;–4;0); (0;2;–3); (3;0;–2).
Задача 3.3. Составить канонические и параметрические уравнения прямой
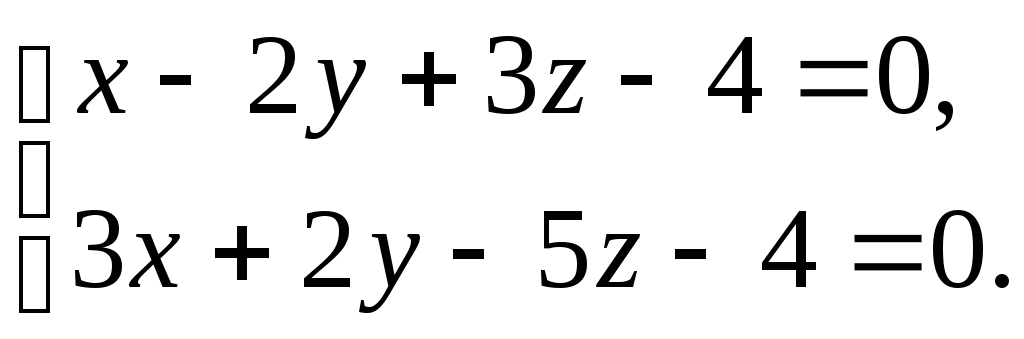
Решение.
Найдём
направляющий вектор данной прямой. Его
можно считать параллельным векторному
произведению нормальных векторов
![]() ,
где
,
где![]() и
и![]() составляющих плоскостей. Итак,
составляющих плоскостей. Итак,
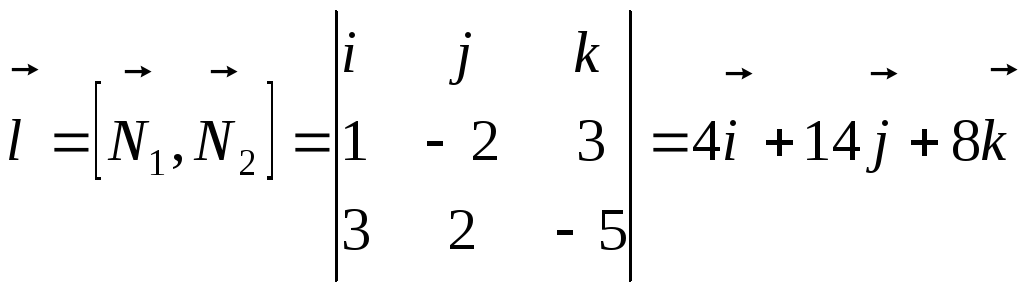 .
.
За
направляющий вектор прямой возьмём
![]() ,
,![]()
Выберем
точку
![]() ,
принадлежащую прямой, так как прямая
не параллельна ни одной из координатных
плоскостей, то в системе
,
принадлежащую прямой, так как прямая
не параллельна ни одной из координатных
плоскостей, то в системе
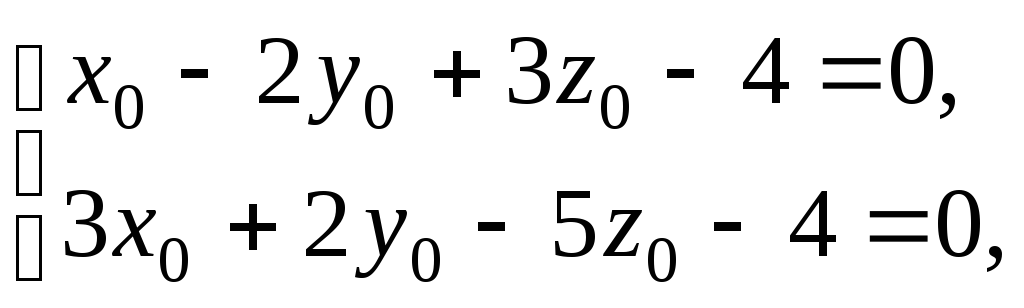
можно
одну из координат
![]() задать произвольно, например, положить
задать произвольно, например, положить![]() ,
что соответствует пересечению прямой
с плоскостьюxОy.
Тогда система примет вид:
,
что соответствует пересечению прямой
с плоскостьюxОy.
Тогда система примет вид:
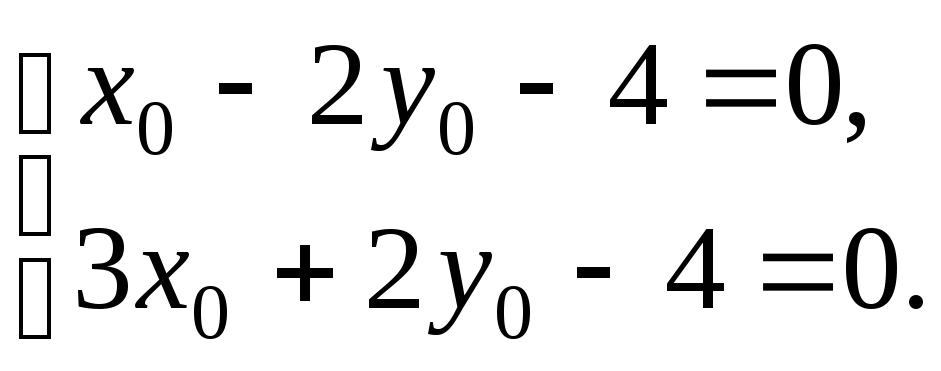
Сложив
оба уравнения, получим
![]() ,
затем найдём
,
затем найдём![]() .
Таким образом, одна из точек прямой
.
Таким образом, одна из точек прямой![]() имеет координаты (2,–1,0). Составим
канонические уравнения прямой:
имеет координаты (2,–1,0). Составим
канонические уравнения прямой:![]() .
Для записи прямой в параметрической
форме приравняем каждую дробь параметруt
и разрешим
относительно переменных x,
y,
z
.
Для записи прямой в параметрической
форме приравняем каждую дробь параметруt
и разрешим
относительно переменных x,
y,
z
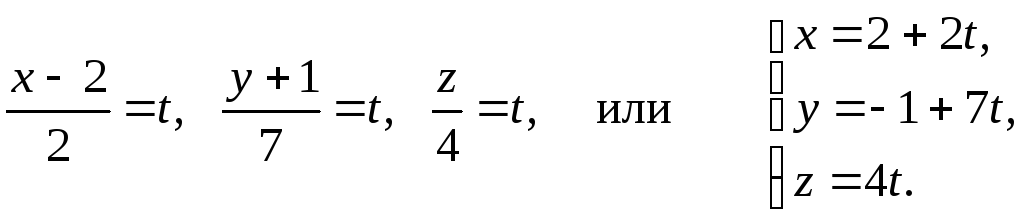
Ответ:
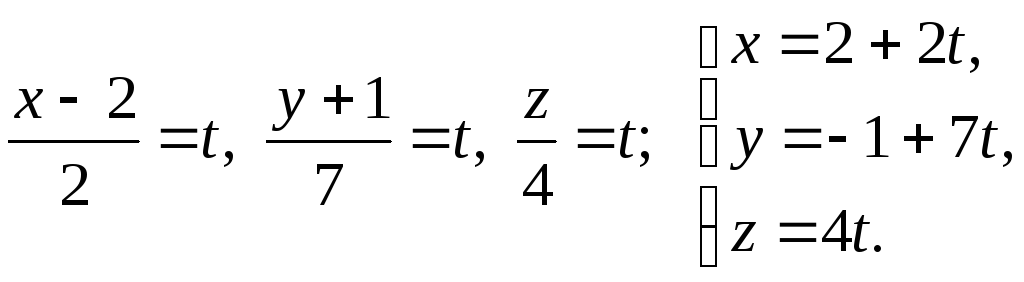
Задача 3.4. Найти угол между прямыми; лежащими в одной плоскости:
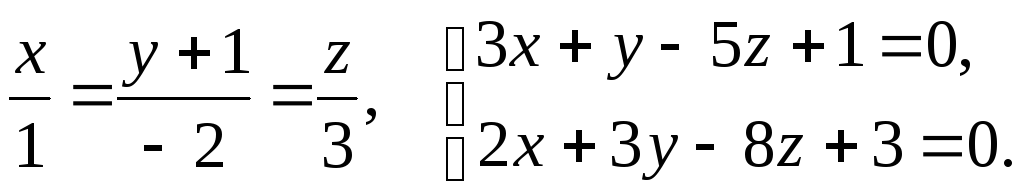
Решение.
Направляющий
вектор первой прямой имеет вид
![]() .
Найдём направляющий вектор второй
прямой
.
Найдём направляющий вектор второй
прямой![]() .
Сначала вычислим векторное произведение
нормальных векторов плоскостей:
.
Сначала вычислим векторное произведение
нормальных векторов плоскостей:
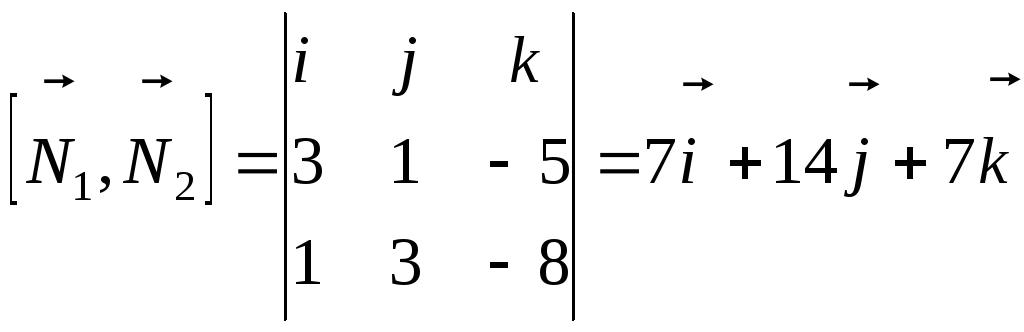 .
.
За
![]() примем вектор
примем вектор![]()
![]() ,
,![]() .
Найдём угол между прямыми по формуле
(3.6)
.
Найдём угол между прямыми по формуле
(3.6)
![]() ,
,
то
есть
![]() ,
прямые перпендикулярны.
,
прямые перпендикулярны.
Ответ:
![]() .
.
Задача 3.5. Доказать, что прямые
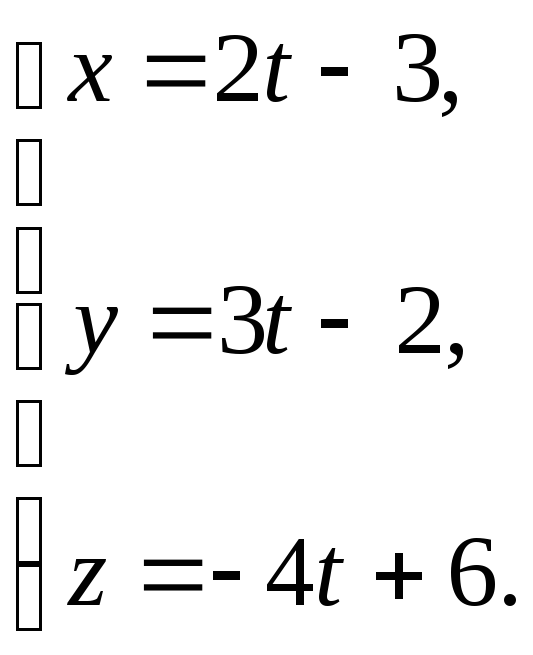 и
и 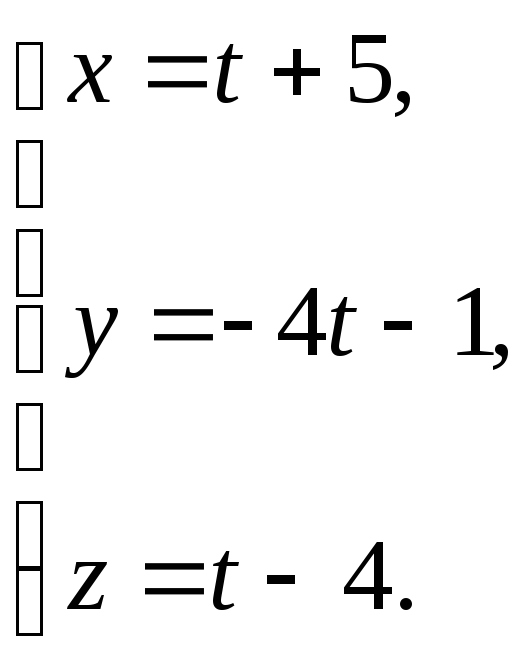
пересекаются.
Решение.
Условие пересечения двух прямых имеет
вид (3.9). В нашем случае
![]() ,
,![]() ,
,![]() ,
,![]() .
Зная точкиМ1
и М2
найдем вектор
.
Зная точкиМ1
и М2
найдем вектор
![]() .
.
Составим определитель по формуле (3.9) и убедимся, что он равен нулю, т.е. вектора пересекаются
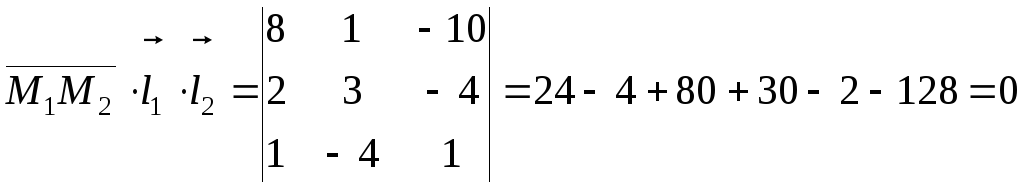 .
.
Ответ. Прямые пересекаются.
Задача
3.6. Составить
уравнение прямой, которая проходит
через точку
![]() перпендикулярно к вектору
перпендикулярно к вектору![]() и пересекает прямую
и пересекает прямую
![]() .
.
Решение.
Для того, чтобы составить канонические
уравнения прямой, надо найти направляющий
вектор
![]() .
Предположим, что координата
.
Предположим, что координата
![]() .
Тогда найдем вектор
.
Тогда найдем вектор![]() ,
удовлетворяющий двум условиям: во-первых,
,
удовлетворяющий двум условиям: во-первых,![]() и
и![]() перпендикулярны, т.е. скалярное
произведение
перпендикулярны, т.е. скалярное
произведение![]() ;
во-вторых, должно выполняться условие
пересечения двух прямых (3.9), причём
;
во-вторых, должно выполняться условие
пересечения двух прямых (3.9), причём![]() ,
,![]() ,
,![]() ,
,
![]() .
.
Запишем эти два условия:
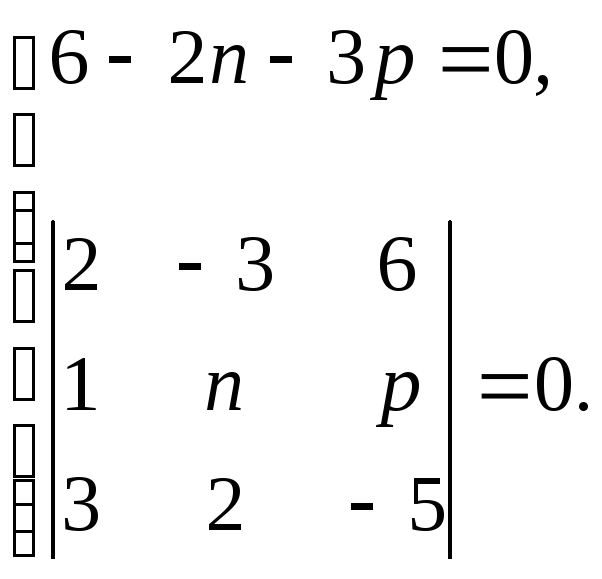 или
или
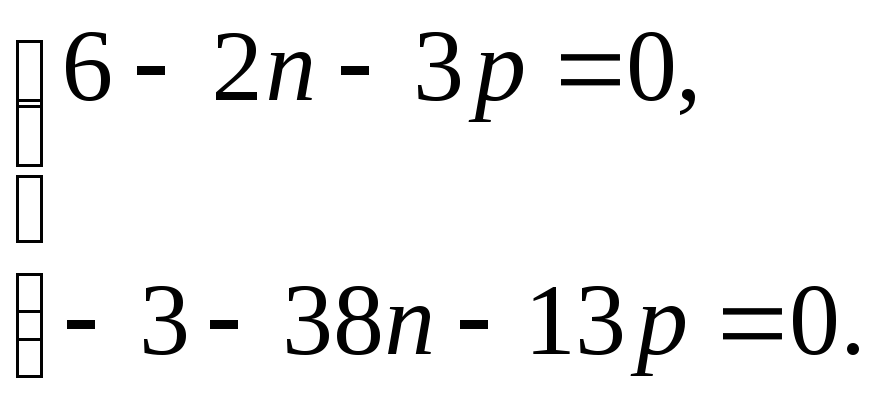
Решаем
последнюю систему, получим
![]() ,
,![]() таким образом,
таким образом,![]() .
За направляющий вектор примем
.
За направляющий вектор примем
![]() .
Искомое уравнение примет вид:
.
Искомое уравнение примет вид:
![]() .
.
Ответ.
![]() .
.
Задача 3.7. Из начала координат опустить перпендикуляр на прямую
![]() .
.
Решение.
Составим уравнение вспомогательной
плоскости, проходящей через начало
координат и перпендикулярной данной
прямой. Направляющий вектор прямой
![]() служит нормальным вектором этой
плоскости, получим
служит нормальным вектором этой
плоскости, получим![]() .
Найдём точку пересечения данной прямой
и плоскости
.
Найдём точку пересечения данной прямой
и плоскости![]() .
Для этого удобно уравнения прямой
записать в параметрической форме и
решить уравнения прямой и плоскости
совместно
.
Для этого удобно уравнения прямой
записать в параметрической форме и
решить уравнения прямой и плоскости
совместно
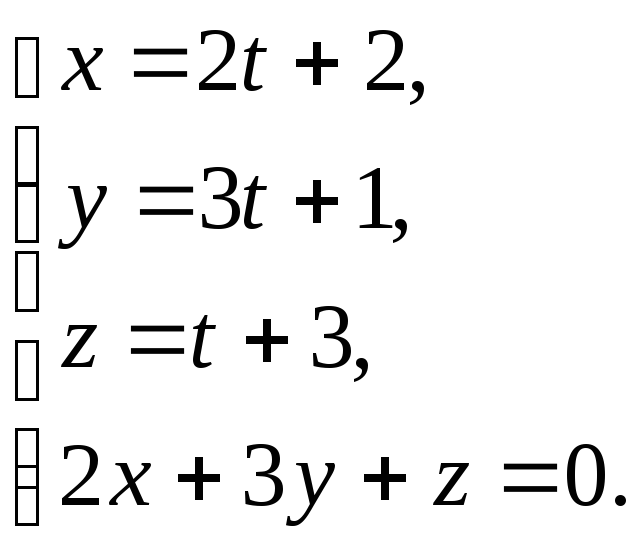
Отсюда
![]() ,
,![]() ,
т.е.
,
т.е.![]() .
Тогда точка пересеченияM
имеет координаты
.
Тогда точка пересеченияM
имеет координаты
![]() (
(![]() подставили в параметрическое уравнение
прямой).
подставили в параметрическое уравнение
прямой).
|
Направляющий
вектор искомой прямой параллелен
радиус-вектору точки M,
т.е. вектору с координатами
Ответ.
|
Рис. 2.21 |
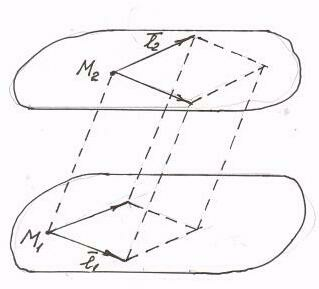
Задача 3.8. Определить кратчайшее расстояние между скрещивающимися прямыми:
![]() ,
, ![]() .
.
Решение.
На скрещивающихся прямых можно построить
параллелепипед с рёбрами
![]() .
Кратчайшее расстояние между прямыми
совпадает с высотой этого параллелепипеда,
площадь основания которого равна
.
Кратчайшее расстояние между прямыми
совпадает с высотой этого параллелепипеда,
площадь основания которого равна![]() .
Поскольку объём параллелепипеда, с
одной стороны, равен
.
Поскольку объём параллелепипеда, с
одной стороны, равен![]() ,
а с другой стороны,
,
а с другой стороны,![]() ,
т.е.
,
т.е.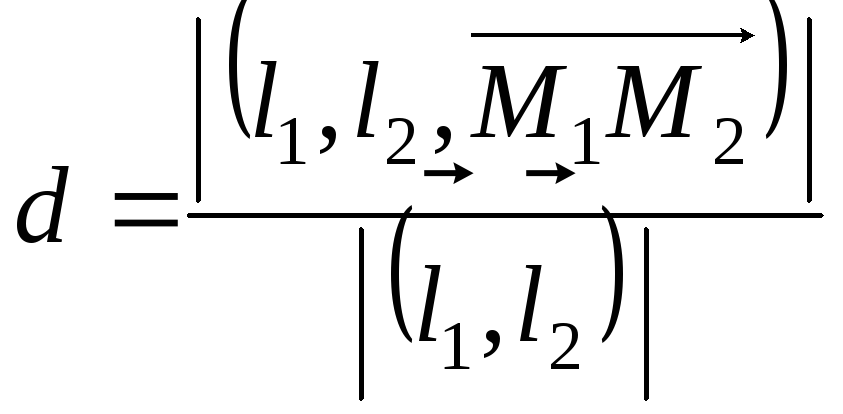 .
.
В
нашем случае
![]() ,
,![]() ,
,![]() ,
,![]() ,
следовательно,
,
следовательно,![]() .
Тогда
.
Тогда
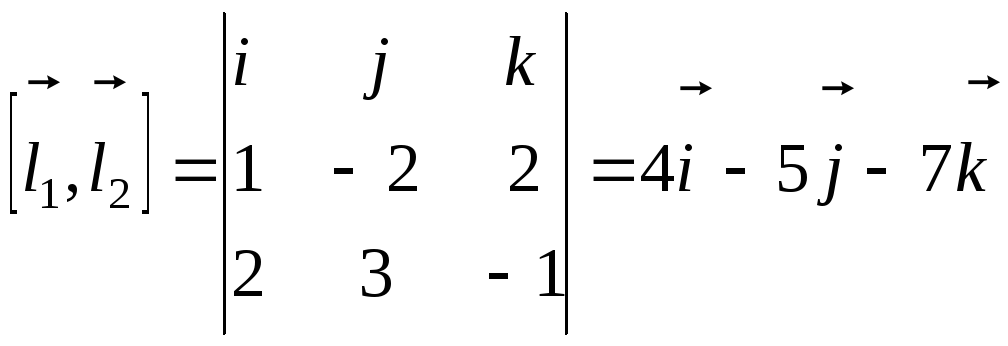 ,
,
![]() .
.
Смешанное произведение
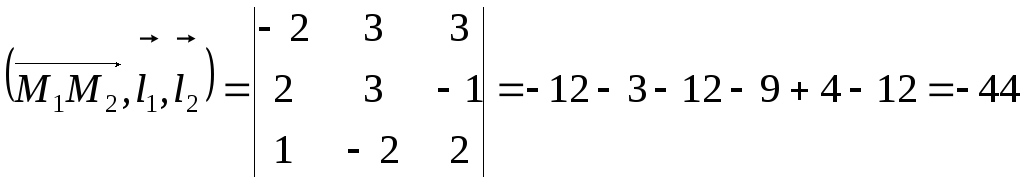 ,
,
т.е.
![]() .
Таким образом, расстояние
.
Таким образом, расстояние![]() .
.
Ответ.
![]() .
.


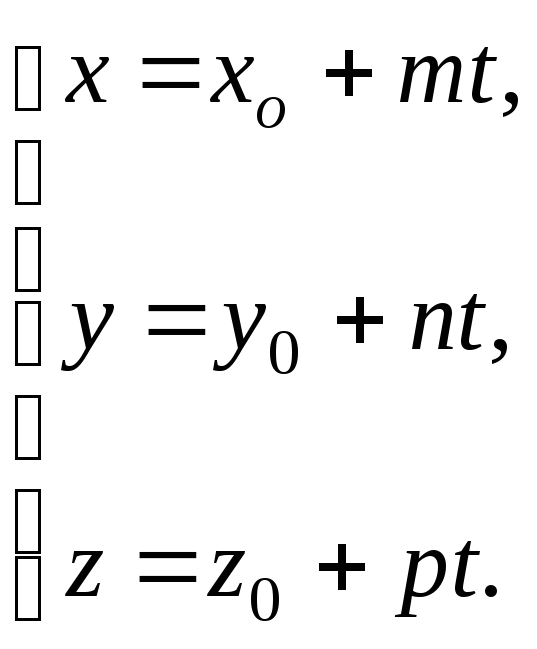 (3.3)
(3.3)
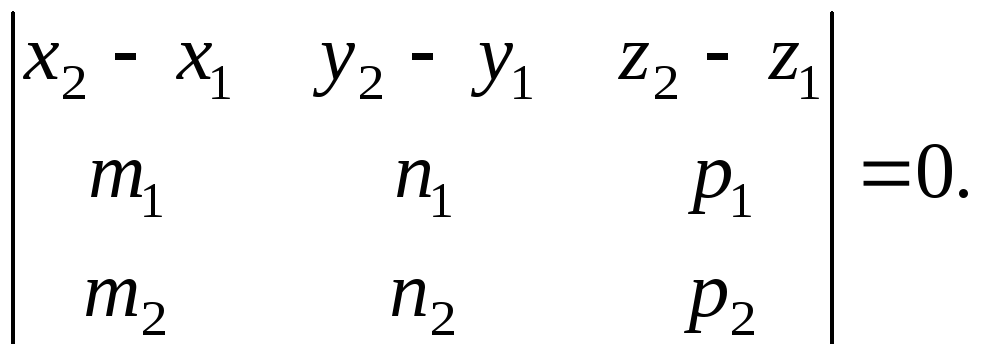 (3.9)
(3.9)