§ 2. Плоскость в пространстве

Основные теоретические сведения

В декартовых координатах каждая плоскость определяется уравнением первой степени, и каждое уравнение первой степени определяет плоскость.

1. Уравнение (2.1)

определяет плоскость, проходящую через точку и имеющую нормальный вектор(рис. 2.13).

Это уравнение называют уравнением связки плоскостей.

Рис. 2.13

Рис. 2.14

2. Уравнение (2.2)

называется общим уравнением плоскости.

3. Уравнение

(2.3)

является уравнением плоскости «в отрезках», здесь величины отрезков, которые плоскость отсекает на координатных осях (рис. 2.14).

4. Нормальным уравнением плоскости называется уравнение вида

, (2.4)

где x, y, z – координаты текущей точки М(x,y,z), принадлежащей плоскости, – направляющие косинусы нормального вектора плоскости,,p – расстояние от плоскости до начала координат.

Обозначая радиус-вектор текущей точки плоскости через . Уравнение (2.4) можно записать в векторной форме:.

Общее уравнение плоскости (2.2) приводится к нормальному виду (2.4) умножением на нормирующий множитель

_(2.5)

знак m берется противоположным знаку свободного члена уравнения (2.2).

5. Отклонение точки от плоскости, заданной нормальным уравнением (2.4), вычисляется по формуле

(2.6)

–расстояние от точки до плоскости, если , тои начало координат находятся по разные стороны плоскости, если– по одну сторону.

Если дано уравнение плоскости в виде (2.2), то удобнее использовать формулу

.

6. Частные случаи расположения плоскости.

Рис. 2.15 Рис. 2.16

Если в общем уравнении плоскости свободный членD=0, то плоскость проходит через начало координат; если какой-либо из коэффициентов A, B, C обращается в нуль, то плоскость параллельна той оси, название которой отсутствует в уравнении, например, плоскость параллельна осиOz (рис. 2.15), плоскость параллельно осиОу (рис.2.16), плоскость параллельна осямOy и Oz, то есть параллельна плоскости yОz. Уравнения x=0, y=0, z=0 представляют координатные плоскости zОy, xОz, xОy соответственно.

7. Угол φ между двумя плоскостями, заданными в общем виде, вычисляется по формуле

.

При получим условие перпендикулярности плоскостей:

.

Условие параллельности двух плоскостей имеет вид: .

8. Уравнение вида (2.7)

где α, β – произвольные числа, не равные нулю одновременно, называется уравнением пучка плоскостей. Это пучок проходит через прямую пересечения плоскостей и(рис. 2.17). Уравнение плоскости проходящей через три данных точки ,,, имеет вид

Рис. 2.17

_.

Примеры решения задач

Задача 2.1. Составить уравнения плоскостей по следующим данным:

а) плоскость перпендикулярна оси Ох и проходит через ;

б) плоскость проходит через ось Оz и точку ,

в) плоскость параллельна оси Ох и проходит через точки

и .

Решение.

а) Так как искомая плоскость перпендикулярна оси Оx, то её нормальный вектор имеет вид .Применяя формулу (2.1),запишем искомое уравнениеили, то есть.

б) Так как плоскость проходит через Оz, то в общем, уравнении (2.2) коэффициенты и, т.е. уравнение имеет вид. Точкапринадлежит плоскости, значит, подстановка координат точки в уравнение плоскости приведёт к тождеству:, отсюдаили, окончательно будем иметь.

в) Плоскость параллельна оси Ox, следовательно, имеет вид . Подставим координаты точеки, получим системурешая которую найдем. После подстановки найденных значенийВ, С в уравнение будем или.

Ответ: а) б)в).

Задача 2.2. Составить уравнение плоскости, проходящей через точку и перпендикулярной плоскостями.

Решение. Нормальные векторы заданных плоскостей имеют вид и. В силу условия задачи, нормальный векторискомой плоскости перпендикулярен векторамиодновременно, поэтому за векторпримем вектор, равный векторному произведению векторови. Таким образом

,

следовательно . Искомое уравнение запишем в виде (2.1)

или .

Ответ. .

Задача 2.3. Вычислить объём пирамиды, ограниченной плоскостью и координатными плоскостями.

Решение.

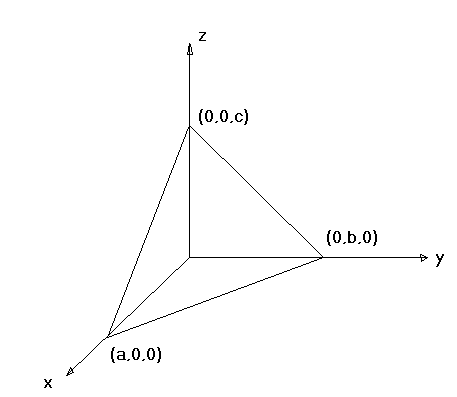
Приведем данное уравнение к уравнению плоскости "в отрезках" (2.3). Для этого перенесем свободный член вправо и разделим обе части уравнения на число

–2, получим . Таким образом, на осях координатOx, Oy, Oz данная плоскость отсекает отрезки, равные соответственно, считая от начала координат. Пирамида имеет вид, изображенный на рис. 2.18.

Рис. 2.18

Пирамида прямая, её объём равен одной шестой от произведения длин этих отрезков, то есть .

Ответ. .

Задача 2.4. Определить, какие из уравнений плоскостей являются нормальными:

а) ,

б) ,

в) .

Решение.

Для уравнение плоскости в нормальной форме (2.4),

и .

Проверим выполнение этих условий:

а) так как р<0, то уравнение не является нормальным;

б) имеем р>0, ,,, но тогда, следовательно, уравнение не является нормальным.

в) здесь р>0, ,,, вычисляя. Уравнение является нормальным.

Задача 2.5. Определить расстояние от плоскости до:

а) начала координат,

б) точки ,

в) точки .

Решение.

Приведем уравнение данной плоскости к нормальному виду (2.4).

Для этого умножим обе части уравнения на нормирующий множитель (2.5), знак которого выбираем отрицательным. Вычислим

.

Уравнение примет нормальную форму . При этомp=2, а p – расстояние от плоскости до начала координат по определению.

а) Расстояние от плоскости до начала координат равно 2.

б) Определим отклонение d по формуле (2.6), где точка имеет координаты (7,0,0). Тогда, следовательно, расстояние от точкидо плоскости равно 4, точкаи начало координат находятся по одну сторону плоскости (<0). То же самое по формуле (2.7): .

в) Определим расстояние от точки до плоскости:Точкаи начало координат расположены по разные стороны (>0).

Самостоятельно найти это же расстояние по формуле (2.7).

Задача 2.6. Доказать, что плоскость пересекает отрезок, ограниченный точкамии.

Решение.

Приведём уравнение к нормальному виду (2.4). При этоми уравнение примет вид

Вычислим отклонения ,точекиот плоскости

_{по формуле (2.6), получим}

т.е. точки илежат по разные стороны от плоскости, следовательно, плоскость пересекает отрезок

_{Задача 2.7. Вычислить расстояние между плоскостями и}

_{Решение. Способ 1. Так как нормальные векторы ; плоскостей имеют пропорциональные координаты}

,

то плоскости параллельны. Чтобы найти расстояние между ними, приведём уравнения плоскостей к нормальному виду, получим и. Так как векторыипротивоположно направлены, то эти плоскости расположены по разные стороны от начала координат на расстоянии 2 исоответственно. Следовательно, расстояние между ними равно.

Способ 2. Выберем на плоскости произвольную точкуМ, например точку пересечения с осью Oz, тогда (нашли из уравнения плоскости).

Теперь задача сводится к нахождению расстояния от точки М(0,0,) до плоскости

.

Ответ. .

Задача 2.8. Вычислить расстояние от точки Р(–1,1,–2) до плоскости, проходящей через три точки ,и.

Решение.

Составим уравнение плоскости, проходящей через три точки:

_{Вычисляя определитель обычным образом (лучше всего разложением по первой строке), получим или}

Приведём это уравнение к нормальному виду. Умножив на нормирующий множитель , будем иметь. Определим отклонениепо формуле (2.6), следовательно, расстояние от точкиР до плоскости равно 4.

Ответ. .

Задача 2.9. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей перпендикулярно плоскости.

Решение. Используя формулу (2.7) составим уравнение пучка плоскостей: . Раскроем скобки, приведём подобные члены, получим. Это уравнение определяет любую плоскость проходящую через прямую пересечения плоскостей. Нормальный вектор имеет вид .

Согласно условно, плоскость с нормальным вектороми искомая плоскость с нормальным векторомперпендикулярны, значит по формуле (2.9). Получим уравнениеили , т.е. . Полученное соотношение подставим в уравнение пучка. Окончательно будем иметь.

Ответ. .

Задача 2.10. Определить, принадлежит ли плоскость пучку плоскостей.

Решение. Преобразуем уравнение пучка плоскостей к виду

и определим, не будет ли противоречива система, полученная при сравнении коэффициентов плоскости пучка и плоскости . Система имеет вид:

Решим ее: , подставам в следующее уравнение, получимили, подставляя в третье уравнение, будем иметьили. Из четвертого уравнения получимили. Таким образом, система противоречива, то есть плоскость не принадлежит пучку плоскостей.