
- •Учебное пособие
- •Аннотация
- •Список сокращений
- •Содержание
- •Введение
- •Научные и технические предпосылки кризисной ситуации.
- •Бурное развитие программного обеспечения.
- •Понятие «защищенная система».
- •1. Основные понятия и определения предмета защиты информации
- •1.1. Общее содержание проблемы информационной безопасности
- •1.2 Информация и информационные отношения. Субъекты информационных отношений
- •1.3. Ценность информации
- •1.4. Модель решетки ценностей
- •1.5. Mls решетка
- •1.6. Определение требований к защищенности информации
- •1.7. Критерии, условия и принципы отнесения информации к защищаемой. Виды конфиденциальной информации.
- •1.8. Выводы
- •1.9. Вопросы для самоконтроля
- •Угрозы информации, методология их выявления и оценки
- •2.1. Санкционированный и несанкционированный доступ
- •2.2. Угрозы информации, методология их выявления и оценки
- •2.3. Ретроспективный анализ подходов к формированию множества угроз информации
- •2.4. Цели и задачи оценки угроз информации в современных системах ее обработки
- •2.5. Система показателей уязвимости информации
- •2.6. Классификация и содержание угроз информации
- •2.7. Методы и модели оценки уязвимости информации
- •2.8. Выводы
- •2.9. Вопросы для самоконтроля
- •3. Общая классификация защитных мер
- •3.1. Базовые свойства безопасности информации. Каналы реализации угроз
- •3.2. Основные принципы обеспечения информационной безопасности
- •3.3. Меры обеспечения безопасности компьютерных систем
- •3.4. Характеристика способов защиты компьютерной информации с помощью аппаратно-программных мер
- •3.5. Выводы
- •3.6. Вопросы для самоконтроля
- •4. Идентификация и аутентификация субъектов
- •4.1. Классификация подсистем идентификации и аутентификации субъектов
- •4.2. Парольные системы идентификации и аутентификации пользователей
- •4.3. Идентификация и аутентификация с использованием индивидуальных биометрических характеристик пользователя
- •4.4. Выводы
- •4.5. Вопросы для самоконтроля
- •5. Элементы теории чисел
- •5.1. Модулярная арифметика
- •5.2. Простые числа и их свойства
- •5.3. Числовые функции
- •5.4. Выводы
- •5.5. Вопросы для самоконтроля
- •6. Методы и средства криптографической защиты
- •6.1. Принципы криптографической защиты информации
- •6.2. Традиционные симметричные криптосистемы
- •6.2.1. Шифрование методом замены
- •6.2.2. Шифрование методами перестановки
- •6.2.3. Шифрование методом гаммирования
- •6.3. Элементы криптоанализа
- •6.4. Современные симметричные системы шифрования
- •6.4.1. Стандарт шифрования des (сша)
- •6.4.2. Отечественный стандарт симметричного шифрования
- •6.5. Асимметричные криптосистемы
- •6.5.1. Недостатки симметричных криптосистем и принципы асимметричного шифрования
- •6.5.2. Однонаправленные функции
- •6.5.3. Алгоритм шифрования rsa
- •6.6. Выводы
- •6.7. Вопросы для самоконтроля
- •7. Контроль целостности информации. Электронно-цифровая подпись
- •7.1. Проблема обеспечения целостности информации
- •7.2. Функции хэширования и электронно-цифровая подпись
- •7.3. Выводы
- •7.4. Вопросы для самоконтроля
- •8. Протоколы безопасной аутентификации пользователей
- •8.1. Аутентификация на основе сертификатов
- •8.2. Процедура «рукопожатия»
- •8.3. Протокол Диффи-Хеллмана
- •8.4. Выводы
- •8.5. Вопросы для самоконтроля
- •9. Управление носителями конфиденциальной информации и внесением изменений.
- •9.1. Носители информации как объект защиты
- •9.2 Разделение тестовой среды и среды промышленной эксплуатации информационной системы. Процесс управления изменениями.
- •9.3. Выводы
- •9.4. Вопросы для самоконтроля
- •10. Разграничение доступа к информации в компьютерных системах
- •10.1. Модели разграничения доступа к информации
- •10.2. Субъектно-объектная модель компьютерной системы в механизмах и процессах коллективного доступа к информационным ресурсам
- •10.2. Монитор безопасности и основные типы политик безопасности
- •10.3. Гарантирование выполнения политики безопасности
- •10.4. Выводы
- •10.5. Вопросы для самоконтроля
- •11. Политики безопасности
- •11.1. Формальные и неформальные политики безопасности
- •11.2. Формальные методы анализа систем
- •11.3. Характеристика моделей безопасности
- •11.4. Выводы
- •11.5. Вопросы для самоконтроля
- •12. Модели безопасности
- •12.1. Модели разграничения доступа
- •12.2. Модели дискреционного доступа
- •12.2.1. Модель дискреционного доступа адепт-50.
- •12.2.2. Пятимерное пространство Хартсона
- •12.2.3. Модель Харрисона-Руззо-Ульмана
- •12.3. Модели мандатного доступа
- •12.3.1. Модель Белла и Лападула
- •12.4. Специализированные модели
- •12.4.1. Модель mms
- •12.5. Проблемы моделей предоставления прав
- •12.6. Информационные модели
- •12.6.1. Модель невмешательства
- •12.6.2. Модель невыводимости
- •12.7. Вероятностные модели
- •12.7.1. Игровая модель
- •12.7.2.Модель системы безопасности с полным перекрытием
- •12.8 .Модели контроля целостности
- •12.8.1. Модель Биба
- •12.8.2. Модель Кларка-Вилсона
- •12.9. Механизмы защиты от угрозы отказа в обслуживании
- •12.9.1. Основные понятия ово
- •12.9.2. Мандатная модель ово
- •12.9.3. Модель Миллена распределения ресурсов (мрр)
- •12.10. Выводы
- •12.11. Вопросы для самоконтроля
- •13. Обзор и сравнительный анализстандартов информационной безопасности
- •13.1. Основные понятия и определения
- •13.2. Критерии безопасности компьютерных систем министерства обороны сша ("Оранжевая книга")
- •13.2.1. Таксономия требований и критериев "Оранжевой книги"
- •13.2.2. Классы безопасности компьютерных систем
- •13.2.3. Интерпретация и развитие "Оранжевой книги"
- •13.3. Европейские критерии безопасности информационных технологий
- •13.3.1. Основные понятия
- •13.3.2. Функциональные критерии
- •13.3.3. Критерии адекватности
- •13.4. Руководящие документы Гостехкомиссии России
- •13.4.1. Основные положения
- •13.4.2. Концепция защиты свт и ас от нсд к информации
- •13.4.3. Показатели защищенности средств вычислительной техники от нсд
- •13.4.4. Показатели защищенности автоматизированных систем от нсд
- •13.5. Федеральные критерии безопасности информационных технологий
- •13.5.1. Цель разработки
- •13.5.2. Основные положения
- •13.5.3. Профиль защиты
- •13.5.4. Этапы разработки Профиля защиты
- •13.5.5. Функциональные требования к ит–продукту
- •13.5.6. Таксономия функциональных требований
- •13.5.7. Ранжирование функциональных требований
- •13.5.8. Требования к технологии разработки ит–продукта
- •13.5.9. Требования к процессу квалификационного анализа ит-продукта
- •13.6. Единые критерии безопасности информационных технологий
- •13.6.1. Цель разработки
- •13.6.2. Основные положения
- •13.6.3. Профиль защиты
- •13.6.4. Проект защиты
- •13.6.5. Требования безопасности
- •13.6.6. Функциональные требования
- •13.6.7. Требования адекватности
- •13.7. Анализ стандартов информационной безопасности
- •13.8. Выводы
- •13.9. Вопросы для самоконтроля
- •Список литературы
- •420111, Г. Казань, ул. К.Маркса, 10
4.4. Выводы
Доступ к любой компьютерной информации в АСОИ, обладающей какой-либо ценностью, должен быть разрешен только определенному кругу лиц, предварительно прошедших регистрацию и подтвердивших свою подлинность. За решение данных задач отвечает подсистема идентификации и аутентификации.
Основным требованием к реализации данной подсистемы является ее стойкость к взлому путем подбора или подмены информации, подтверждающей подлинность пользователя (пароля, ключа, и т.д.). Информация, подтверждающая подлинность пользователя должна храниться в секрете, лучше – на внешнем аппаратном устройстве, максимально защищенном от НСД.
4.5. Вопросы для самоконтроля
Что понимают под идентификацией и аутентификацией? В чем заключается различие данных этапов и как они связаны между собой?
Приведите примеры различных идентификаторов и аутентификаторов пользователя.
Что понимают под авторизацией пользователя?
Чем определяется стойкость к взлому подсистемы идентификации и аутентификации?
Перечислите основные недостатки парольных подсистем идентификации и аутентификации.
Перечислите основные угрозы парольным подсистемам идентификации и аутентификации.
Перечислите требования к выбору и использованию паролей?
Как количественно оценить стойкость к взлому парольных подсистем идентификации и аутентификации?
Как изменится стойкость к взлому подсистемы парольной аутентификации при увеличении характеристик A,L,V,T? При их уменьшении?
Приведите примеры технических устройств, с помощью которых может решаться задача идентификации пользователя?
Приведите примеры технических устройств, с помощью которых может решаться задача идентификации и аутентификации пользователя?
Что понимается под биометрической аутентификацией пользователя? Приведите примеры биометрических характеристик.
Перечислите основные отличия методов биометрической аутентификации пользователя от других (например, парольных).
Что из себя представляет вектор биометрических признаков?
Что понимают под коэффициентом ошибочных отказов и коэффициентом ошибочных подтверждений биометрической системы?
Дайте геометрическую интерпретацию коэффициентов ошибочных отказов и ошибочных подтверждений.
Как в биометрических системах принимается решение о прохождении либо не прохождении пользователем аутентификации?
Что из себя представляет кривая рабочих характеристик приемника?
5. Элементы теории чисел
При решении задач шифрования, дешифрования, построения ключевых систем в криптографии, используется представление обрабатываемого текста как целых чисел. Это дает возможность использовать математику целых чисел для создания стойких систем. Элементы теории целых чисел и рассматриваются в данной главе.
5.1. Модулярная арифметика
Пусть m – целое число. Тогда при делении любых целых чисел на m возможно получение ровно m остатков – 0,1,2,…,m-1.
Определение 5.1. Целые числа a и b называют сравнимыми по модулю m, если их разность a-b делится без остатка на m, или, что то же самое, остатки, получаемые при делении чисел a и b на m, равны между собой. В этом случае число b называют вычетом числа a по модулю m.
Если a
сравнимо с b
по модулю m,
то это записывают как
![]() .
.
Пример 5.1
Целые числа 17 и
12 сравнимы между собой по модулю 5, то
есть
![]() ,
кроме этого
,
кроме этого![]() .
.
Существует бесконечное количество чисел, сравнимых с числом a по модулю m, но только одно из них расположено в диапазоне от 0 до m-1.
Обычно, для целого
числа a>0
предпочитают использовать вычеты
![]() .
Набор целых чисел от 0 до (m-1)
называют полным
набором вычетов по модулю m.
.
Набор целых чисел от 0 до (m-1)
называют полным
набором вычетов по модулю m.
Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Целые числа по модулю m по отношению к операциям сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности.
Основные свойства сравнений:
Рефлексивность:
 .
.Симметричность:
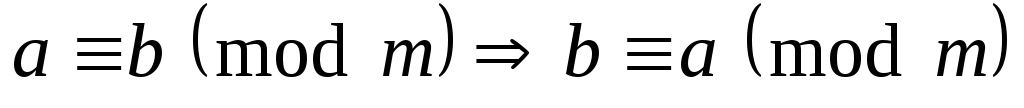 .
.Транзитивность:
 .
.Если
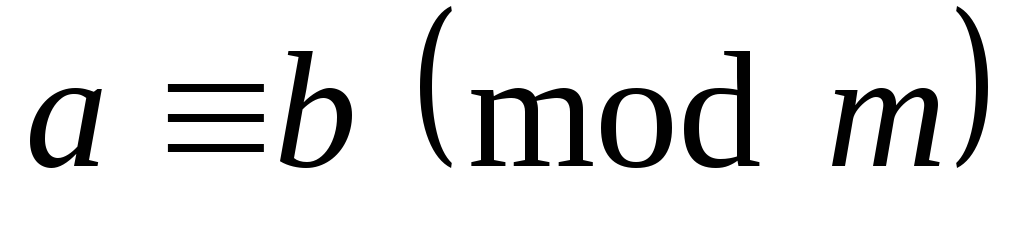 ,
,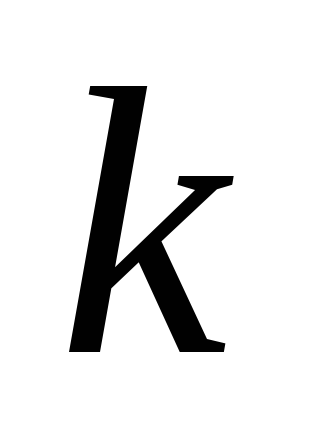 - произвольные целое число, то
- произвольные целое число, то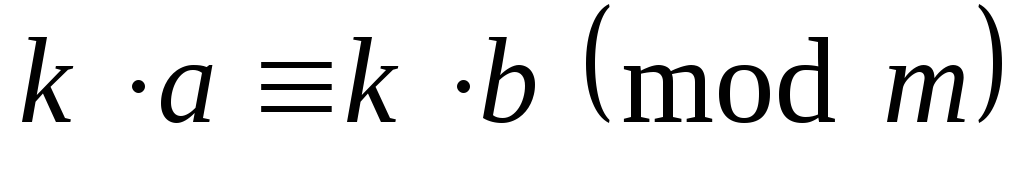 .
.Если
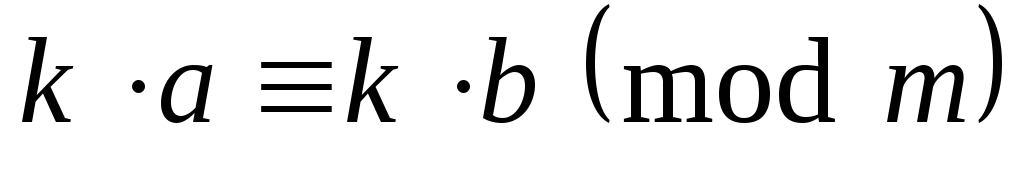 ,
наибольший общий делитель
,
наибольший общий делитель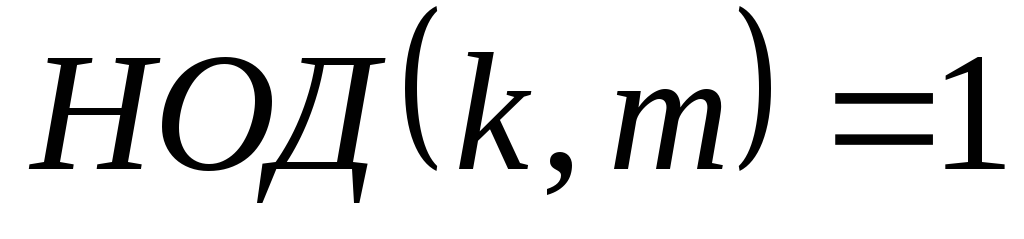 ,
то
,
то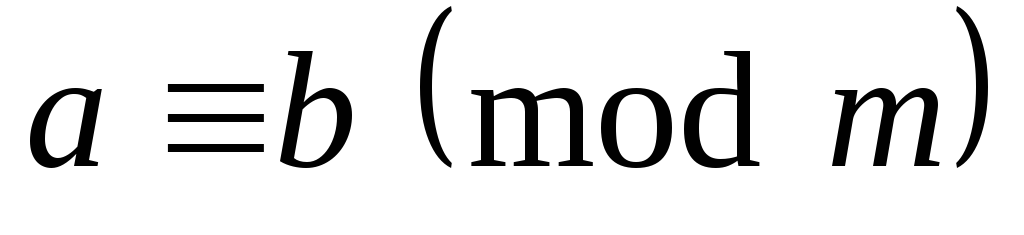 .
.Если
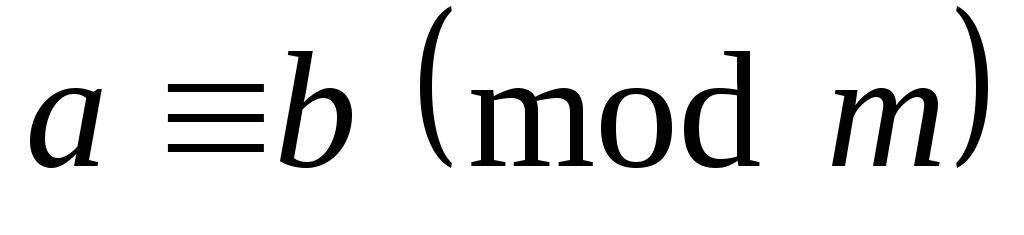 ,
,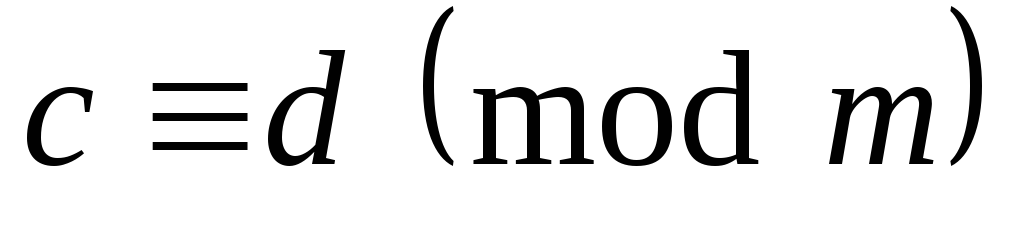 ,
то
,
то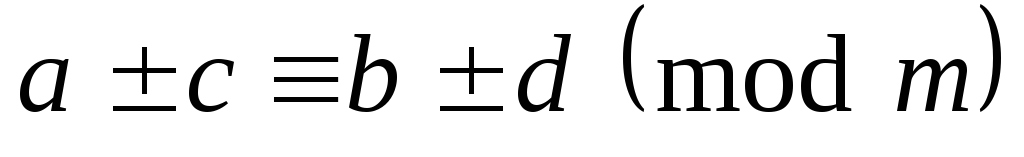 .
.Если
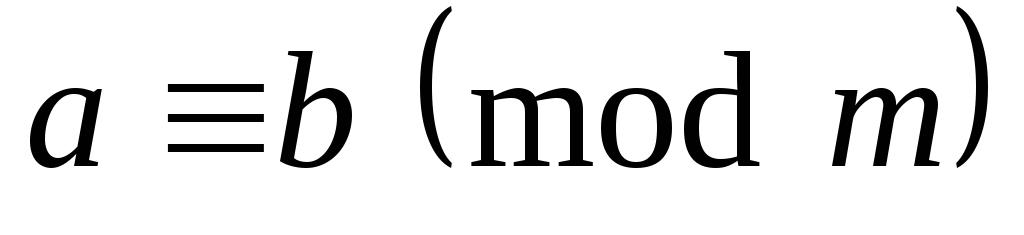 ,
,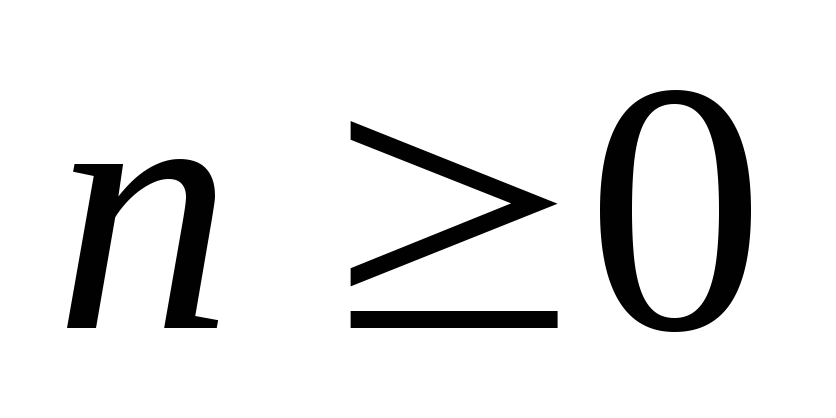 ,
то
,
то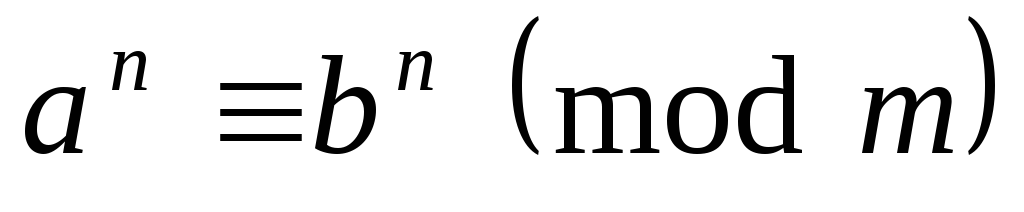 .
.Если
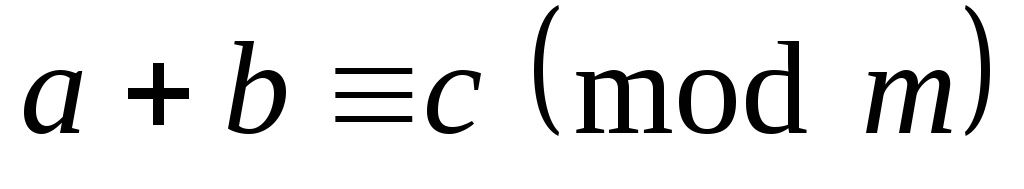 ,
то
,
то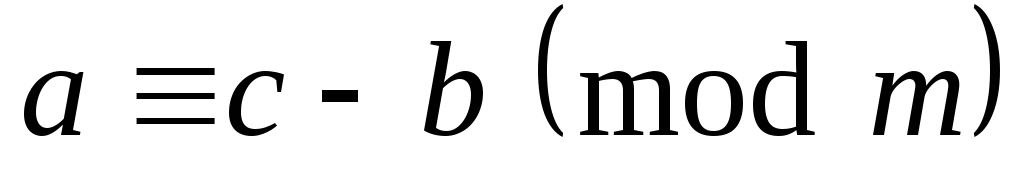 .
.Если
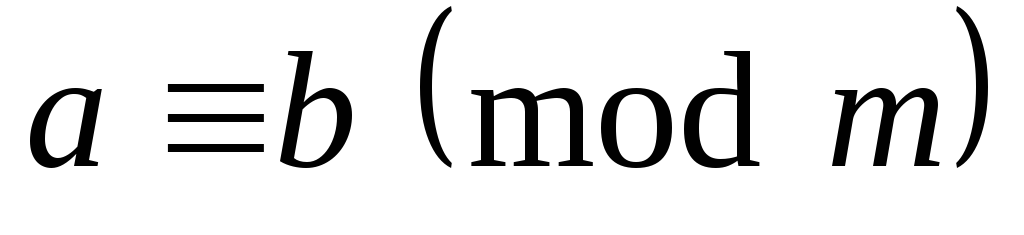 ,
,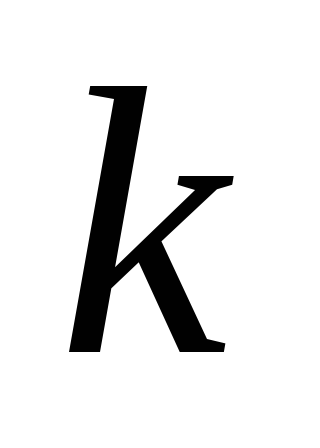 - произвольные целое число, то
- произвольные целое число, то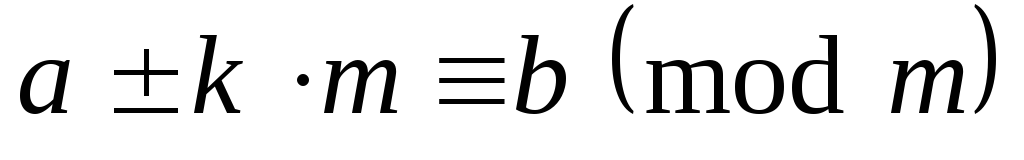 .
.
При выполнении арифметических операций по модулю, можно либо сначала приводить операнды по модулю m, а затем выполнять операции, либо сначала выполнять операции, а затем приводить результат по модулю m.
В криптографии используется множество вычислений по модулю m, так как с вычислениями по модулю удобнее работать в связи с ограничением диапазона всех промежуточных величин и результата. Кроме того, решение задач вида вычисления дискретных логарифмов трудно в вычислительном плане.
Для модуля m длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2k бит. Поэтому такую операцию, как возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов.
Возведение числа
a
в степень x
по модулю m,
то есть нахождение
![]() можно легко выполнить как ряд умножений.
Особенно легко возводить в степень по
модулю, если
можно легко выполнить как ряд умножений.
Особенно легко возводить в степень по
модулю, если![]() - степень двойки.
- степень двойки.
Пример 5.2
Пусть, например,
требуется вычислить
![]() .
В этом случае не следует выполнять
серию умножений и одно приведение по
модулю большого числа. Вместо этого
выполняют три малых умножения и три
малых приведения по модулю.
.
В этом случае не следует выполнять
серию умножений и одно приведение по
модулю большого числа. Вместо этого
выполняют три малых умножения и три
малых приведения по модулю.
![]()
Например,
![]()
![]()
Вычисление
![]() ,
гдеx
не является степенью двойки, немного
сложнее. В этом случае степень x
представляют в двоичной форме и
представляют x
как сумму степеней двойки.
,
гдеx
не является степенью двойки, немного
сложнее. В этом случае степень x
представляют в двоичной форме и
представляют x
как сумму степеней двойки.
Пример 5.3
Пусть x=25(10)=11001(2), тогда 25=24+23+20.
Тогда
![]()
![]() .
.
Поскольку многие алгоритмы шифрования основаны на возведении в большую степень больших чисел по большому модулю, целесообразно использовать рассмотренные выше алгоритмы быстрого возведения в степень.
