§3. Теорема о совместимости (слау)

В общем виде система линейных алгебраических уравнений с n неизвестными x₁, x₂, ..., x_n записывается так:

(1)

Кратко СЛАУ (1) может быть записана так:

(2)

или

где

A=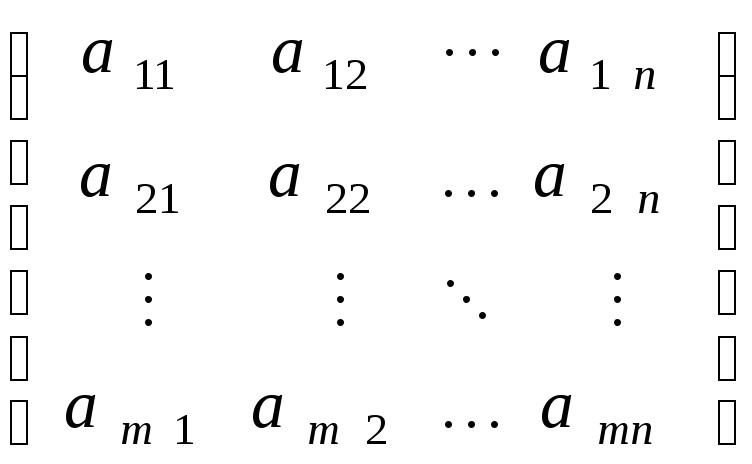, (3)

ОПРЕДЕЛЕНИЕ 1. Если присоединить к матрице А столбец свободных членов, то получится матрица , которая называетсярасширенной матрицей СЛАУ (1):

A=(4)

Из определения матрицы A СЛАУ (1) и расширенной матрицы ясно, что их рангиилибо равны между собой, либо рангна единицу больше, чем. Вопрос о совместности СЛАУ (1) решается с помощью теоремы Кронекера-Капелли.

ТЕОРЕМА 1. СЛАУ (1) совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу матрицыA, то есть когда

ПРИМЕР. Исследовать на совместимость следующую СЛАУ:

Составим матрицу данной системы и вычислим ее ранг:

поскольку то.

Далее , составим расширенную матрицу системы

Так как а окаймляющий его минор

то

Итак, то есть данная система совместна.

СЛЕДСТВИЕ 1. Если СЛАУ (1) совместна и ранг матрицы A системы (1) равен числу неизвестных п, то система имеет единственное решение.

СЛЕДСТВИЕ 2. Если система (1) совместна и ранг матрицы меньше числа неизвестныхn, то система имеет бесчисленное множество решений.

ТЕОРЕМА 2.Система n линейных уравнений с n неизвестными, определитель которой отличен от нуля всегда совместна и имеет единственное решение, вычисляемое по формулам

где

,

.

.

4. Решение неоднородной слау из m уравнений с n неизвестными

Пусть дана система m линейных алгебраических уравнений с n неизвестными (1). Пусть ranqA= ranq, то есть система совместна. Не ограничиваясь общностью, будем считать, что базисный минор располагается в первыхстроках и столбцах матрицы A. Отбросив последниеm-r уравнений системы (1), запишем укороченную систему

(2)

которая эквивалентна исходной.

Назовем неизвестные x₁ ,x₂ , ..., x_r базисными, а x_r+1 , ..., x_n- свободными. Перенесем слагаемыe, содержащие свободные неизвестные, в правую часть уравнения (2). В результате, получим систему линейных алгебраических уравнений относительно базисных неизвестных

(3)

которая для каждого набора значений свободных неизвестных x_r+1= c₁, x_r+2= c₂, ..., x_n=c_n-r. имеет единственное решение: x₁= f₁,(c₁, c₂ , ..., c_n-r), x₂= f₂,(c₁, c₂ , ..., c_{n-r), ...,} x_r= f_r,(c₁, c₂ , ..., c_{n-r). Решение системы (3) можно} определить либо по методу Крамера, либо методом Гаусса.

Общее решение СЛАУ можно записать в виде матрицы-столбца следующим образом:

(4)

Однородная система линейных алгебраических уравнений из m уравнений с n неизвестными

Пусть дана однородная СЛАУ, состоящая из m линейных уравнений с n неизвестными

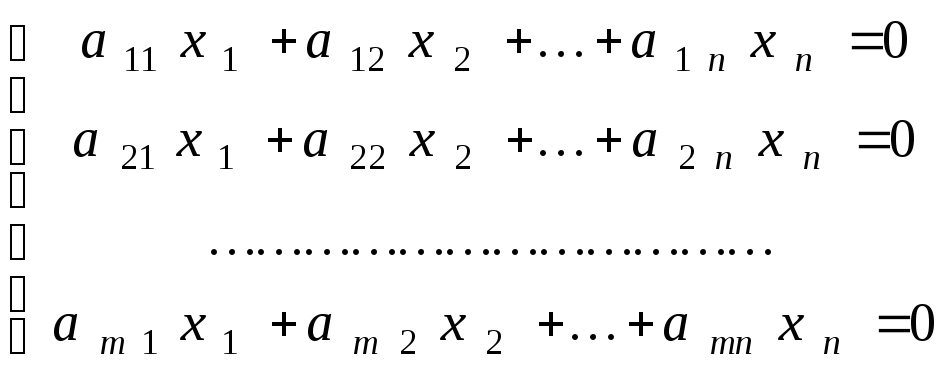. (1)

Отметим, что добавление столбца из нулей не изменяет ранга матрицы СЛАУ (1). Поэтому на основании теоремы Кронекера-Капелли эта система всегда совместна и имеет, по крайней мере, нулевое решение (x₁ =x₂ = ...,= x_n=0). Если определитель системы (1) отличен от нуля и число уравнений равно числу неизвестных, то по теореме Крамера, нулевое решение является единственным.

Рассмотрим теперь другой случай, когда ранг матрицы СЛАУ (1) меньше числа неизвестных, то есть r(A)<n. Тогда данная система кроме нулевого решения может иметь и ненулевые решения. Для нахождения этих решений нужно в системе (1) выделить r линейно независимых уравнений, а остальные отбросить. В выделенных уравнениях в левой части оставляем r базисных неизвестных, а остальные n-r свободных неизвестных переносим в правую часть. В результате, приходим к системе

(2)

решение которой можно определить по формулам Крамера или Гаусса.

В данной системе имеем r базисных неизвестных x₁, x₂,..., x_r и n-r - свободных неизвестных: x_r+1, x_r+2 , ..., x_n . Система (2) имеет бесчисленное множество решений. Однако, среди этого множества есть решения линейно независимые между собой.

ОПРЕДЕЛЕНИЕ. Фундаментальной системой решения СЛАУ называются n-r линейно независимых решений однородной системы уравнений.

ПРИМЕР. Дана однородная система уравнений

Найти ее общее решение и фундаментальную систему уравнений.

Ш а г 1. Вычислим ранг матрицы системы, используя элементарные преобразования:

а) отбрасываем 2-й столбец, так как он пропорционален 1-му;

б) 3-й столбец сначала умножим на (-2) и прибавим ко 2-му, а затем умножим его на (-3) и сложим с 1-м, умножим на 2;

в) отбрасываем 1-й столбец, так как он пропорционален 2-му;

г) 1-й столбец умножим на 3 и прибавим ко 2-му;

д) 1-ю строку умножим на 5 и прибавим к 4-й;

е) отбрасываем 3-ю строку и делим 1-ю на (-1), а 2-ю - на 2.

Имеем

Так как r(A)=2, то есть r  min(m,n), то данная система имеет фундаментальную систему решений, число которых n-2=4-2=2.

Определим теперь общее решение системы. Для этого определим базисный минор, то есть минор второго порядка, отличный от нуля. Таким минором является, например, минор, составленный из коэффициентов при x₃ и x₄ в первом и втором уравнениях системы: Оставляя базисные неизвестныеx₃ и x₂ в левой части и перенося свободные неизвестные x₁ и x₂ в правую часть, приходим к системе

Ее решение, которое определим по формулам Крамера, имеет вид:

Чтобы получить фундаментальную систему решений нужно найти любые два линейно независимых решения данной системы. Полагая сначала x₁ = 1, x₂ =0, имеем x₃ =-2,5; x₄ =3,5; полагая затем x₁ =0, x₂ =1, получим x₃ =5, x₄ =-7.

Таким образом, фундаментальная система решений имеет вид

,

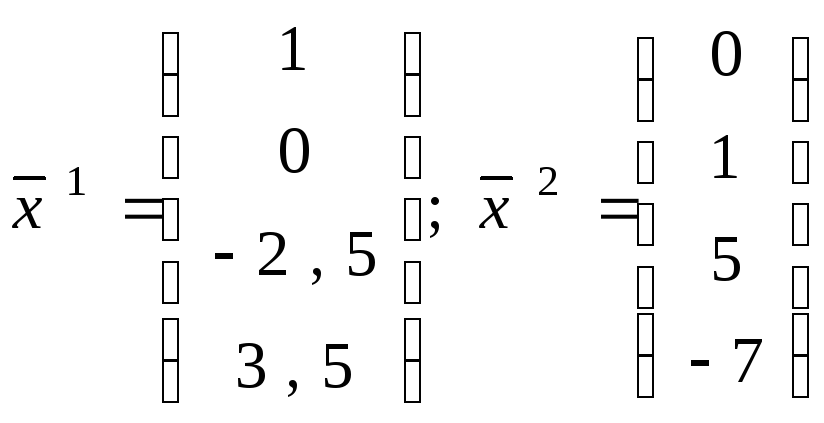а общее решение , гдес₁ и с₂ - произвольные числа.