Г л а в а П. СИСТЕМА ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ

Уравнений (слау)

§1. Определение и матричная запись (слау)

В этой главе будут рассмотрены линейные системы алгебраических уравнений. Эти СЛАУ появляются во многих областях прикладной математики. Например, при нахождении приближенных решений дифференциальных и интегральных уравнений, которые описывают различные процессы в физике, химии, биологии и экономике. Размерность СЛАУ, как правило, является большой и зависит от сложности решаемой проблемы. Так, в теории электрических сетей количество уравнений равно количеству ячеек сети и т.д.

В общем виде система линейных алгебраических уравнений с n неизвестными x₁, x₂, ..., x_n записывается так:

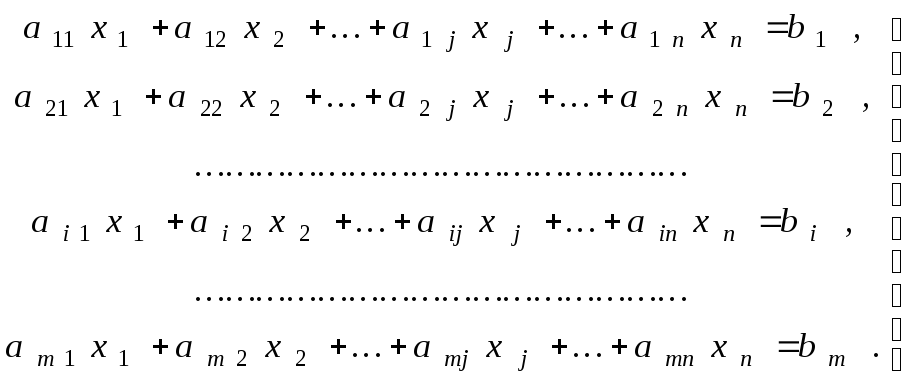(1)

Коэффициенты при неизвестных обозначаются черезa_ij, где первый индекс i указывает номер уравнения, в котором находится данный коэффициент, а второй индекс j - номер неизвестного, при котором находится данный коэффициент.

Например, коэффициент a₄₅ находится в четвертом уравнении при неизвестном x₅.

Числа b₁, b₂, ..., b_m в системе (1) называются свободными членами в СЛАУ (1).

ОПРЕДЕЛЕНИЕ 1. Решением СЛАУ (1) называется любая совокупность чисел c₁, c₂, ..., c_n, которая будучи подставленной на место неизвестных x₁, x₂, ..., x_n в уравнения данной системы , обращает все эти уравнения в тождество.

ОПРЕДЕЛЕНИЕ 2. СЛАУ (1) называется совместной, если она имеет решение, и несовместной, если не имеет решения.

Совместная слау может иметь одно или несколько решений и называется

определенной, если имеет одно решение, и неопределенной, если имеет несколько решений.

ОПРЕДЕЛЕНИЕ 3. Две СЛАУ с одним и тем же числом неизвестных называются эквивалентными, если они или обе несовместны, или обе совместны и имеют одни и те же решения.

Так следующие элементарные преобразования переводят данную СЛАУ в эквивалентную:

а) перестановка двух уравнений системы;

б) умножение обеих частей уравнения системы на любое, отличное от нуля число;

в) прибавление (вычитание) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число, отличное от нуля.

ОПРЕДЕЛЕНИЕ 4. СЛАУ, в которой все свободные члены b₁, b₂, ..., b_n равны нулю называется однородной СЛАУ.

Матрицей A СЛАУ (1) называется матрица, составленная из коэффициентов при неизвестных этой системы

A=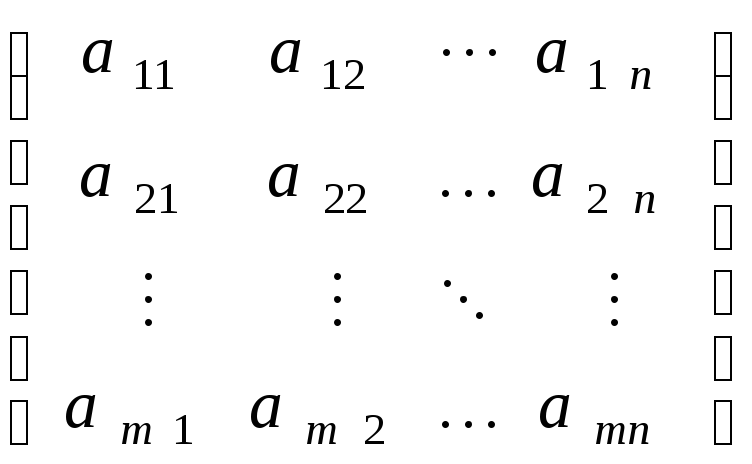. (2)

Используя понятие матрицы A СЛАУ (1) и матриц-столбцов, введенных соотношениями:

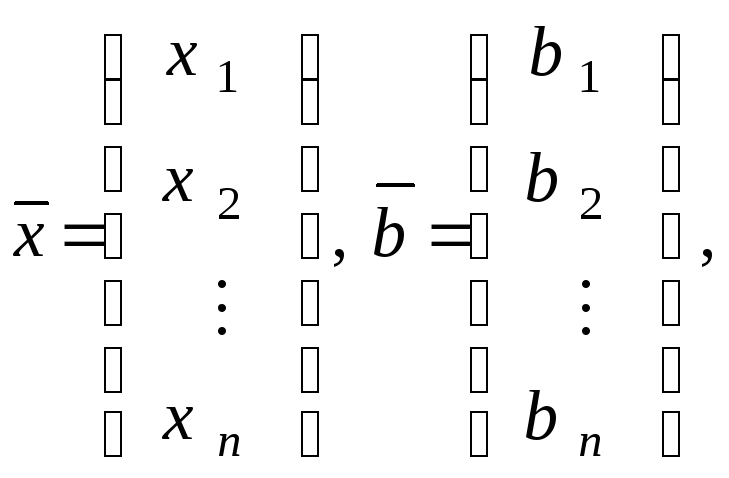(3)

запишем систему (1) следующим образом

(4)

Из вида записи (4) следует, что первая компонента векторавычисляется как произведение первой строки матрицы A на вектор-столбец .

Приравнивая полученное выражение первой компоненте матрицы-столбца B, получим первое уравнение системы (1)

a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n = b₁

Второе уравнение СЛАУ (1) получается, если вторую строку матрицы A умножить на матрицу-столбец и приравнять полученное соотношение второму элементу матрицы и т.д.

Пример. Записать в матричной форме следующую СЛАУ:

Матрица A для этой системы имеет вид

а матрицы-столбцы запишутся так

Тогда матричная запись исходной системы будет иметь вид

или

§2. Прямые методы решения систем линейных алгебраических уравнений

Итак, пусть требуется решить систему линейных алгебраических уравнений

(1)

Напомним, что в (1.1) A -квадратная матрица с вещественными коэффициентамиa_ij -заданный вектор-столбец с вещественными компонентами, - искомый вектор-столбец сn-компонентами.

Прежде чем применить какой-либо метод решения задачи (1) следует убедиться в том, что эта задача поставлена корректно. Будем говорить, что задача поставлена корректно, если:

а) решение задачи существует,

б) единственно,

в) непрерывно зависит от входных данных.

Как известно, для задачи (1) первые два требования в определении будут выполнены, если

Третье же требование в (2) применительно к задаче (1) нуждается в некоторой детализации и связано с понятием обусловленности исходной матрицы A.

Методы решения СЛАУ (1) можно разделить на две группы: прямые и итерационные. В прямых методах нахождение решения задачи (1) осуществляется за конечное число действий. В итерационных методах определяется не само решение задачи (1) , а некоторая последовательность векторов (k- номер итерации) такая, что

(2)

К прямым методам решения определенных СЛАУ относятся: метод Крамера и метод Гаусса. Причем эти методы различаются по числу действий, необходимых для нахождения решения исходных СЛАУ. Мерой различия может служить число действий, необходимое для вычисления одного неизвестного. Ниже рассмотрим оба эти метода.