
- •ЛинейнОе пространство
- •Определения. Базис и размерность. Разложение вектора по базису пространства
- •Определение базиса и размерность пространства l
- •Если обладает базисом, то говорят, что линейное пространствоLимеет рангQ (ranq q).
- •Изоморфизм n-мерных линейных пространств
- •Формулы преобразования координат при изменении базиса
- •Произведением. Евклидово пространство
- •2.1. Определение евклидова пространства. Длина вектора. Неравенство Коши-Буняковского
- •2.2. Ортогональный и орто-нормированный базисы в пространстве е
- •2.3. Ортогонализация базиса в пространстве
- •2.4. Скалярное произведение векторов в евклидовом пространстве
- •Изоморфизм евклидовых пространств
- •§ 3. Билинейные квадратичные формы
- •4.1. Линейная функция
- •4.2. Билинейные формы
- •4.3. Матрицы билинейной формы
- •4.4. Преобразование матрицы билинейной формы при изменении базиса
- •4.5. Квадратичные формы
- •4.6. Методы приведения квадратичной формы к каноническому виду
- •Будем рассматривать квадратичную форму (7) в евклидовом пространстве
4.3. Матрицы билинейной формы
Выберем в n-мерном
пространстве
![]() какой-либо базис
какой-либо базис![]() и выразим билинейную форму
и выразим билинейную форму
![]() через коэффициенты
через коэффициенты
![]() и
и![]() векторов
векторов
![]() и
и
![]() в этом базисе. Имеем:
в этом базисе. Имеем:
![]()
В силу свойств а)
и б) пункта
![]() билинейной формы, имеем:
билинейной формы, имеем:

Или, короче:
![]() .
.
Обозначим постоянные
![]() через
через![]() .
Тогда в заданном базисе
.
Тогда в заданном базисе![]() всякая билинейная форма вn-мерном
пространстве может быть записана в
виде:
всякая билинейная форма вn-мерном
пространстве может быть записана в
виде:
![]() .
(5)
.
(5)
ОПРЕДЕЛЕНИЕ 4.
Матрицу
![]()
![]() ,
составленную из коэффициентов
,
составленную из коэффициентов![]() многочлена (5), называютматрицей
билинейной формы
многочлена (5), называютматрицей
билинейной формы
![]() в
базисе
в
базисе
![]()
Таким образом, в
каждом базисе пространства
![]() билинейная форма
билинейная форма
![]() определяется своей матрицей:
определяется своей матрицей:
 .
.
4.4. Преобразование матрицы билинейной формы при изменении базиса
Пусть даны в
n-мерном
линейном пространстве
![]() два базиса:
два базиса:![]() и
и![]() .
Причем, векторы второго базиса
.
Причем, векторы второго базиса![]() выражаются через векторы базиса
выражаются через векторы базиса![]() формулами:
формулами:
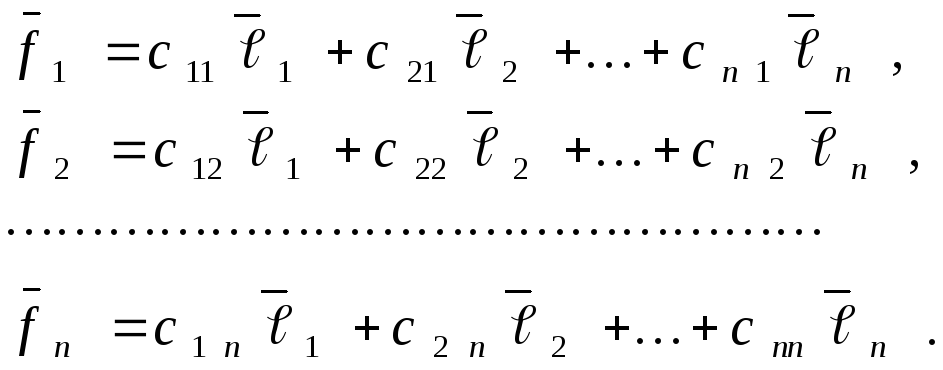
Матрицу

назовем матрицей
перехода от базиса
![]() к базису
к базису![]() .
.
Пусть
![]()
![]() есть матрица билинейной формы
есть матрица билинейной формы
![]() в базисе
в базисе
![]() ,
а
,
а![]() матрица той же билинейной формы в базисе
матрица той же билинейной формы в базисе![]() .
Наша задача состоит в том, чтобы по
матрице
.
Наша задача состоит в том, чтобы по
матрице![]()
![]() найти матрицу
найти матрицу![]()
![]() .
.
По определению
![]() ,
то есть
,
то есть![]() - значение билинейной формы
- значение билинейной формы
![]() при
при
![]() .
.
Для того, чтобы
найти это значение, то есть
![]() , воспользуемся формулой (5), подставив
в нее вместо
, воспользуемся формулой (5), подставив
в нее вместо![]() и
и![]() координаты векторов
координаты векторов![]() и
и![]() в
базисе
в
базисе![]() ,
то есть числа
,
то есть числа![]() и
и![]() .
Получим:
.
Получим:
![]() .
(6)
.
(6)
Это и есть искомая формула.
Запишем ее в
матричной форме. Для этого положим
![]() .
Таким образом,
.
Таким образом,![]() является элементами матрицы
является элементами матрицы![]() ,
транспонированной к матрицеС.
С учетом этого выражение (6) можно записать
так:
,
транспонированной к матрицеС.
С учетом этого выражение (6) можно записать
так:
![]()
или
![]() .
.
Итак, если А
и В
суть матрицы билинейной формы
![]() соответственно в базисах
соответственно в базисах
![]() и
и![]() .,
то преобразование матрицы билинейной
формы при переходе от одного базиса к
другому будет иметь вид:
.,
то преобразование матрицы билинейной
формы при переходе от одного базиса к
другому будет иметь вид:
![]()
где С- матрица
перехода от базиса![]() к базису
к базису![]() .,
а
.,
а![]() - транспонированная матрица.
- транспонированная матрица.
4.5. Квадратичные формы
Пусть -![]() симметричная
билинейная форма.
симметричная
билинейная форма.
ОПРЕДЕЛЕНИЕ 1.
Функция
![]() ,
которая получается из билинейной формы
,
которая получается из билинейной формы
![]() ,
если положить в ней
,
если положить в ней
![]() =
=![]() ,
называется квадратичной
формой.
,
называется квадратичной
формой.
Всякая квадратичная
форма
![]() ,
в базисе
,
в базисе
![]() евклидового пространстваЕn
выражается следующей формулой:
евклидового пространстваЕn
выражается следующей формулой:
![]() ,
(7)
,
(7)
где
![]()
![]() симметричная матрица
симметричная матрица![]() квадратичной
формы и
квадратичной
формы и![]() .
.
В некотором базисе
выражение (7) квадратичной формы может
не содержать произведений
![]() ,
то есть
,
то есть
![]() ,
(8)
,
(8)
Выражение (8)
называется каноническим видом квадратичной
формы. В частности, если
![]() ,
то получаемнормальный
вид
квадратичной
формы
,
то получаемнормальный
вид
квадратичной
формы
![]() .
.
Для всякой квадратичной формы существует такой базис, в котором она имеет канонический вид.
4.6. Методы приведения квадратичной формы к каноническому виду
а) Метод Лагранжа выделения полных квадратов.
Пусть квадратичная
форма![]() имеет в базисе
имеет в базисе
![]() вид (7). Для приведения формы
вид (7). Для приведения формы
![]() к сумме квадратов методом Лагранжа
рассмотрим случай квадратичной формы,
у которой все коэффициенты
к сумме квадратов методом Лагранжа
рассмотрим случай квадратичной формы,
у которой все коэффициенты
![]() (при квадратах
(при квадратах
![]() ),
),
![]() равны нулю и в то же время эта квадратичная
форма не равна тождественно нулю, то
есть в ней есть отличное от нуля хотя
бы одной произведение, например,
равны нулю и в то же время эта квадратичная
форма не равна тождественно нулю, то
есть в ней есть отличное от нуля хотя
бы одной произведение, например,
![]() .
.
Выполним преобразование базиса, при котором коэффициенты векторов в старом и новом базисах связаны формулами:
 .
.
Тогда:
![]() .
.
Таким образом,
всегда найдется такой базис, в котором
в записи (7) хотя бы один коэффициент
при квадрате
![]() .отличен
от нуля.
.отличен
от нуля.
В дальнейшем будем
считать, что
![]() .
(Если
.
(Если![]() ,
то отличен от нуля коэффициент при
квадрате какой-нибудь другой координаты
и к рассматриваемому случаю можно
прийти, иначе, занумеровав векторы
,
то отличен от нуля коэффициент при
квадрате какой-нибудь другой координаты
и к рассматриваемому случаю можно
прийти, иначе, занумеровав векторы![]() ,
что также является некоторым преобразованием
базиса).
,
что также является некоторым преобразованием
базиса).
Рассмотрим часть
квадратичной формы, содержащей
![]() ,
то есть
,
то есть
![]() .
.
Дополним эту сумму до полного квадрата:
![]() ,
,
где
![]() есть алгебраическая сумма членов, не
зависящих от
есть алгебраическая сумма членов, не
зависящих от![]() .
Если теперь сделать замену
.
Если теперь сделать замену
![]()
то квадратичная форма в новом базисе примет вид
 .
.
В полученной форме
выделено слагаемое
![]() ,
а оставшаяся частьА,
является квадратичной формой в
,
а оставшаяся частьА,
является квадратичной формой в
![]() .
.
Далее эти рассуждения
повторяются для исходной квадратичной
формы
![]() и т.д. Конечным результатом является
то, что она приводится к нормальной
форме.
и т.д. Конечным результатом является
то, что она приводится к нормальной
форме.
ПРИМЕР 1. Методом Лагранжа привести к каноническому виду квадратичную форму
![]() .
.
Первое преобразование:
![]() .
.
Тогда получим:
 .
.
Второе преобразование:
![]() .
.
Получим новое выражение для квадратичной формы:
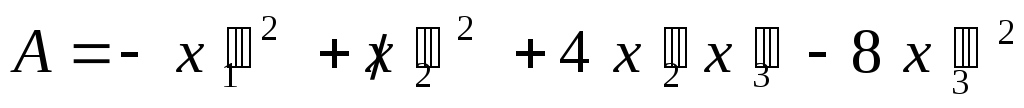 .
.
Третье преобразование:
![]() .
.
форма примет канонический вид:
 .
.
При этом
 .
.
б) Метод собственных векторов.
